Pressure in fluids

Pressure in fluids

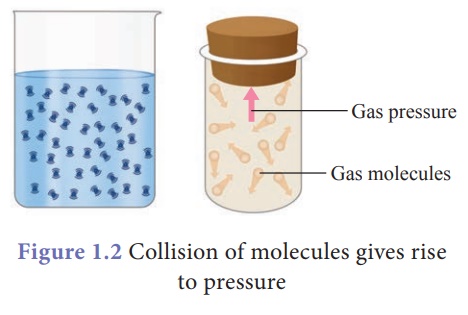
All the flowing substances, both liquids and gases are called fluids. Like solids, fluids also have weight and therefore exert pressure. When filled in a container, the pressure of the fluid is exerted in all directions and at all points of the fluid. Since the molecules of a fluid are in constant, rapid motion, particles are likely to move equally in any direction. Therefore the pressure exerted by the fluid acts on an object from all directions. It is shown in Figure 1.2. Pressure in fluids is calculated as shown below.

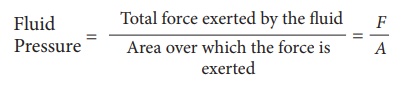
We shall first learn about the pressure exerted by liquids and then learn about the pressure exerted by gases.

1. Pressure due to liquids

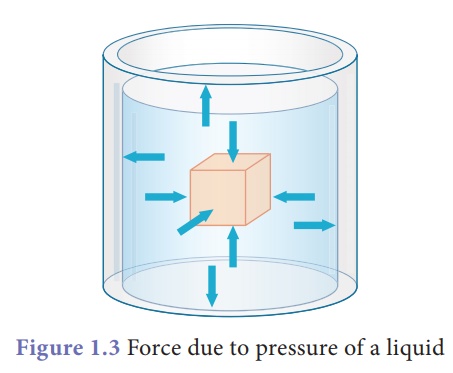
The force exerted due to the pressure of a liquid on a body submerged in it and on the walls of the container is always perpendicular to the surface. In Figure 1.3, we can see the pressure acting on all sides of the vessel.

When an air filled balloon is immersed inside the water in a vessel it immediately comes up and floats on water. This shows that water (or liquid) exerts pressure in the upward direction. It is shown in Figure 1.4.

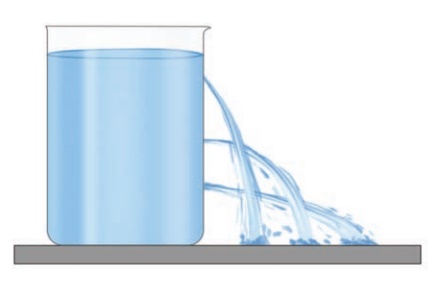
Similarly, liquid pressure acts in lateral sides also. When a bottle having water is pierced on the sides we can see water coming out with a speed as in Figure 1.5. This is because liquid exerts lateral pressure on the walls the container.

2. Factors determining liquid pressure in liquids

Pressure exerted by a liquid at a point is determined by,

(i) depth (h)

(ii) density of the liquid (ρ)

(iii) acceleration due to gravity (g).

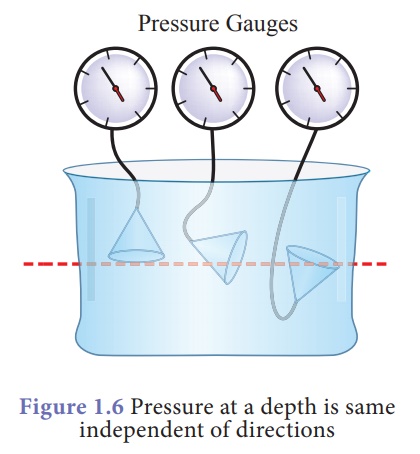
From this activity we can see that pressure varies as depth increases. But, it is same at a particular depth independent of the direction. In Figure 1.6, we see the gauge reads the same value because the pressure is being measured at the same depth (red line).

3. Pressure due to a liquid column

A tall beaker is filled with liquid so that it forms a liquid column. The area of cross section at the bottom is A. The density of the liquid is ρ. The height of the liquid column is h. In other words the depth of the water from the top level surface is 'h' as shown in Figure 1.7.

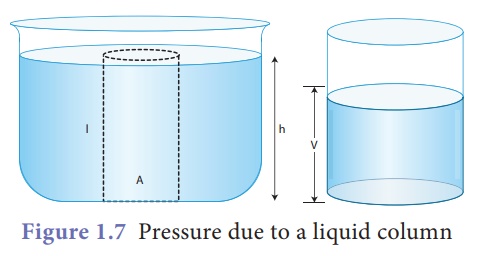
We know that thrust at the bottom of the column (F) = weight of the liquid.               

Therefore, F = mg            …..(1)

We can get the mass of the liquid by multiplying the volume of the liquid and its density.         

Mass, m = ρ V                ….. (2)

Volume of the liquid column, V = Area of cross section (A) × Height (h) = Ah   (3)

Substituting (3) in (2)   

Hence, mass, m = ρAh   (4)

Substituting (4) in (1)   

Force = mg = ρAhg

∴Pressure due to a liquid column, P = hρg

This expression shows that pressure in a liquid column is determined by depth, density of the liquid and the acceleration due to gravity. Interestingly, the final expression for pressure does not have the term area A in it. Thus pressure at a given depth does not depend upon the shape of the vessel containing the liquid or the amount of liquid in the vessel. It only depends on the depth. In Figure 1.8, the pressure is the same even though the containers have different amounts of liquid in them, and are of different shapes.

Example 1.2

Calculate the pressure exerted by a column of water of height 0.85 m (density of water, ρ_w = 1000 kg m^–3) and kerosene of same height (density of kerosene, ρk = 800 kg m^–3)

Solution:

Pressure due to water

= hρ_wg = 0.85 m × 1000 kg m^–3 × 10 m s^–2

= 8500 Pa.

Pressure due to kerosene

= hρ_kg = 0.85 m × 800 kg m^–3 × 10 ms^–2

= 6800 Pa.