Chapter: Civil : Principles of Solid Mechanics : Torsion
PrandtlŌĆÖs Stress Function
PrandtlŌĆÖs Stress
Function
An alternative solution procedure that
leads to a much simpler boundary condition, but a somewhat more difficult field
equation, involves the intro-duction of a stress function ŽĢ(x,y)
defined as:
By this definition, the equilibrium
Equation (9.10) is automatically solved and the boundary condition Equation
(9.15) becomes:
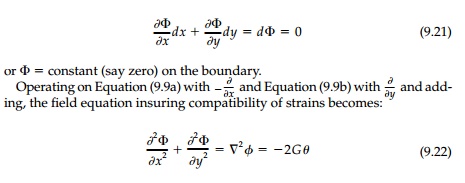
As noted in previews, this is a Poisson
equation for which a solution can always be found and the boundary condition
is particularly nice.
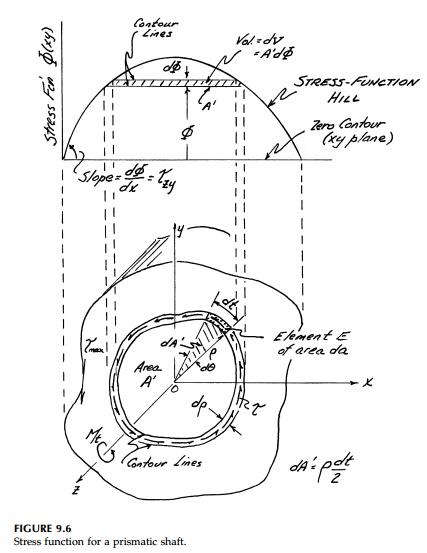
However, the power of the Prandtl stress function approach is in visualiz-ing torsional shear fields. It is easy to show that the stress function ŽĢ will transform in any direction as an invariant scalar function, and therefore in a new coordinate orientation x', y'
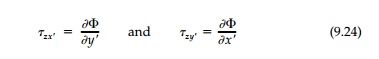
Thus at any point the shear stress in one direction is equal in magnitude to the slope of the ŽĢ surface in the perpendicular direction, and the maximum shear is the maximum slope of the stress function curve and acts tangent (along a contour) to that curve. If we visualize the stress function plotted in the z direction above the cross-section, then contours (of equal ŽĢ) can be plot-ted and:
a. The
shear Žä acts along these contours and is
proportional to the shortest distance (slope normal) to the next contour;
b. Žämax
occurs where the stress-hill contours become closest togeth-er, which will be
on the boundary of the cross-section (generally where r = Rt(x2+y2) is a minimum.
From Figure 9.6 it is
easy to show that the twisting moment Mt is propor-tional to
the volume of this stress-function hill. The shear force dS on a differ
ential element E will be
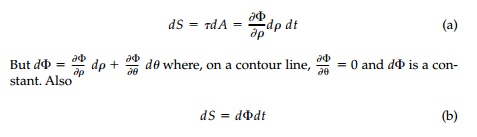
Therefore, between two
contour lines the resisting moment

which is twice the
volume of the stress-function hill.
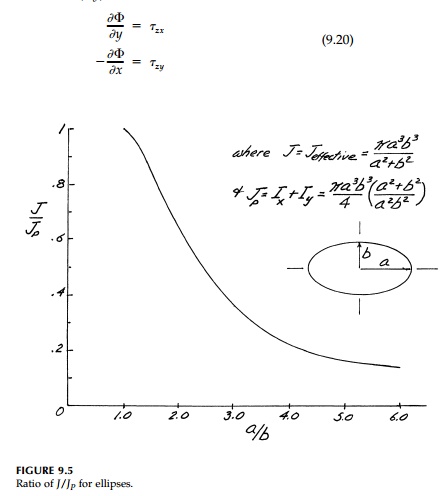
For example, consider
the elliptic cross-section discussed previously. Assume a stress function

which must satisfy
Equation (9.22), and the boundary condition ŽĢedge
=
0. The volume of the stress-function hill (a paraboloid) is 0.5 ŽĆ abh and therefore:
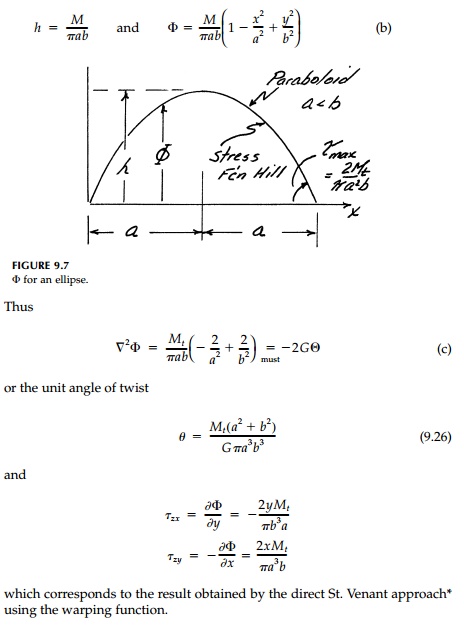
which corresponds to
the result obtained by the direct St. Venant approach* using the warping
function.
Related Topics