Chapter: Communication Theory : Angle Modulation
Phase Modulation
PHASE MODULATION:
Phase
Modulation (PM) is another form of angle modulation. PM and FM are closely
related to each other. In both the cases, the total phase angle θ of the modulated signal varies.
In an FM wave, the total phase changes due to the change in the frequency of
the carrier corresponding to the changes in the modulating amplitude.
In PM,
the total phase of the modulated carrier changes due to the changes in the
instantaneous phase of the carrier keeping the frequency of the carrier signal
constant. These two types of modulation schemes come under the category of
angle modulation. However, PM is not as extensively used as FM.
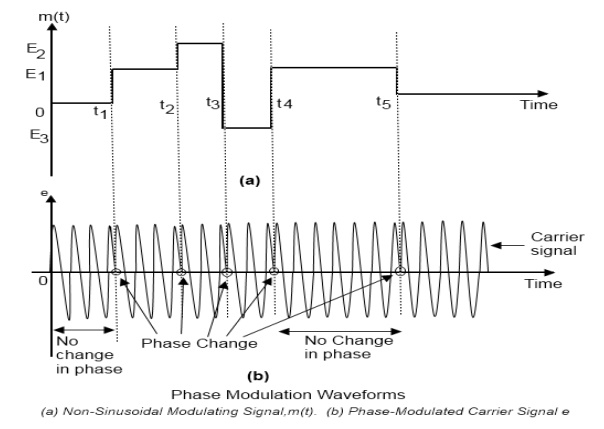
At time
t1, the amplitude of m(t) increases from zero to E1. Therefore, at t1, the
phase modulated carrier also changes corresponding to E1, as shown in Figure
(a). This phase remains to this attained value until time t2, as between t1 and
t2, the amplitude of m(t) remains constant at El. At t2, the amplitude of m(t)
shoots up to E2, and therefore the phase of the carrier again increases
corresponding to the increase in m(t). This new value of the phase attained at
time t2remains constant up to time t3. At time t3, m(t) goes negative and its
amplitude becomes E3. Consequently, the phase of the carrier also changes and
it decreases from the previous value attained at t2. The decrease in phase
corresponds to the decrease in amplitude of m(t). The phase of the carrier
remains constant during the time interval between t3 and t4. At t4, m(t) goes
positive to reach the amplitude El resulting in a corresponding increase in the
phase of modulated carrier at time t4. Between t4 and t5, the phase remains
constant. At t5 it decreases to the phase of the unmodulated carrier, as the
amplitude of m(t) is zero beyond t5.
ü Equation of a PM Wave:
To derive
the equation of a PM wave, it is convenient to consider the modulating signal
as a pure sinusoidal wave. The carrier signal is always a high frequency
sinusoidal wave. Consider the modulating signal, em and the carrier signal ec, as given by, equation 1 and 2,
respectively.
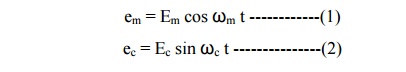
The
initial phases of the modulating signal and the carrier signal are ignored in
Equations (1) and (2) because they do not contribute to the modulation process
due to their constant values. After PM, the phase of the carrier will not
remain constant. It will vary according to the modulating signal em maintaining
the amplitude and frequency as constants. Suppose, after PM, the equation of
the carrier is represented as:

Where θ, is the instantaneous phase
of the modulated carrier, and sinusoid ally varies in proportion to the
modulating signal. Therefore, after PM, the instantaneous phase of the
modulated carrier can be written as:
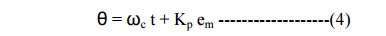
Where, kp is the constant of
proportionality for phase modulation. Substituting Equation (1) in Equation
(4), yon get:

In
Equation (5), the factor, kpEm is defined as the modulation index, and is given
as:
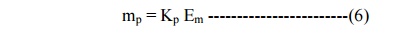
where,
the subscript p signifies; that mp is the modulation index of the PM wave.
Therefore, equation (5) becomes
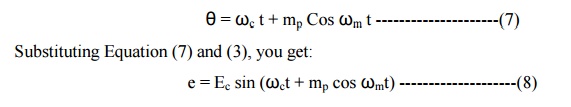
Related Topics