Narrow Band FM Modulation

NARROW BAND FM MODULATION:

The case where |θm(t)| << 1 for all t is called narrow band FM. Using the approximations cos x ~= 1 and sin x ~= x for |x| << 1, the FM signal can be approximated as:

s(t) = Ac cos[ωct + θm(t)]

= Ac cos ωct cos θm(t) − Ac sin ωctsin θm(t)

~= Ac cos ωct − Acθm(t) sin ωct

or in complex notation

s(t) = ACRE{e^jwct (1 + jθm(t) }

This is similar to the AM signal except that the discrete carrier component Ac coswc(t) is 90° out of phase with the sinusoid Ac sinwc(t) multiplying the phase angle θm(t). The spectrum of narrow band FM is similar to that of AM.

^ü   The Bandwidth of an FM Signal:

The following formula, known as Carson‘s rule is often used as an estimate of the FM signal bandwidth: BT = 2(∆f + fm) Hz

where ∆f is the peak frequency deviation and fm is the maximum baseband message  frequency component.

^ü   FM Demodulation by a Frequency Discriminator:

A frequency discriminator is a device that converts a received FM signal into a voltage that is proportional to the instantaneous frequency of its input without using a local oscillator and, consequently, in a non coherent manner.

• When the instantaneous frequency changes slowly relative to the time-constants of the filter, a quasi-static analysis can be used.

• In quasi-static operation the filter output has the same instantaneous frequency as the input but with  an  envelope  that  varies  according  to  the  amplitude  response  of  the filter  at the instantaneous frequency. 

• The amplitude variations are then detected with an envelope detector like the ones used for AM demodulation. 

^ü   An FM Discriminator Using the Pre-Envelope:

When θm(t) is small and band-limited so that cos θm(t) and sinθm(t) are essentially band-limited signals with cut off frequencies less than fc, the pre-envelope of the FM signal is

s+(t) = s(t) + jˆs(t) = Acej(ωct+θm(t))

The angle of the pre-envelope is φ'(t) = arctan[ˆs(t)/s(t)] = ωct + θm(t)

The derivative of the phase is =ωct+ kθm(t)

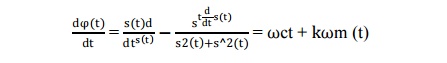
which is exactly the instantaneous frequency. This can be approximated in discrete-time by using FIR filters to form the derivatives and Hilbert transform. Notice that the denominator is the squared envelope of the FM signal.

This formula can also be derived by observing,

The bandwidth of an FM discriminator must be at least as great as that of the received FM signal which is usually much greater than that of the baseband message. This limits the degree of noise reduction that can be achieved by preceding the discriminator by a bandpass receive filter.

^ü   Using a Phase-Locked Loop for FM Demodulation:

A device called a phase-locked loop (PLL) can be used to demodulate an FM signal with better performance in a noisy environment than a frequency discriminator. The block diagram of a discrete-time version of a PLL as shown in figure,

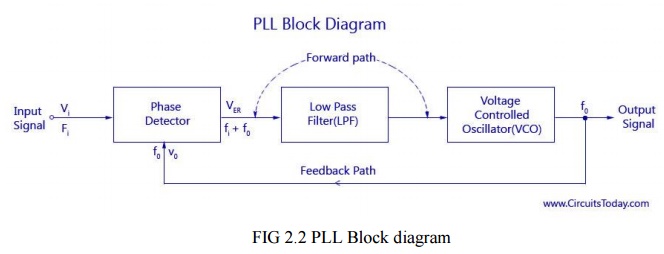
The block diagram of a basic PLL is shown in the figure below. It is basically a flip flop consisting of a phase detector, a low pass filter (LPF),and a Voltage Controlled Oscillator (VCO) The input signal Vi with an input frequency fi is passed through a phase detector. A phase detector

basically a comparator which compares the input frequency fiwith the feedback frequency fo .The phase detector provides an output error voltage Ver (=fi+fo),which is a DC voltage. This DC voltage is then passed on to an LPF. The LPF removes the high frequency noise and produces a steady DC level, Vf (=Fi-Fo). Vf also represents the dynamic characteristics of the PLL.

The DC level is then passed on to a VCO. The output frequency of the VCO (fo) is directly proportional to the input signal. Both the input frequency and output frequency are compared and adjusted through feedback loops until the output frequency equals the input frequency. Thus the

PLL works in these stages – free-running, capture and phase lock.

As the name suggests, the free running stage refer to the stage when there is no input voltage applied. As soon as the input frequency is applied the VCO starts to change and begin producing an output frequency for comparison this stage is called the capture stage. The frequency comparison stops as soon as the output frequency is adjusted to become equal to the input frequency. This stage is called the phase locked state.

^ü   Comments on PLL Performance:

• The frequency response of the linearized loop characteristics of a band-limited differentiator.

• The loop parameters must be chosen to provide a loop bandwidth that passes the desired aseband message signal but is as small as possible to suppress out-of-band noise.

• The PLL performs better than a frequency discriminator when the FM signal is corrupted by additive noise. The reason is that the bandwidth of the frequency discriminator must be large enough to pass the modulated FM signal while the PLL bandwidth only has to be large enough to pass the baseband message. With wideband FM, the bandwidth of the modulated signal can be significantly larger than that of the baseband message.

^ü   Bandwidth of FM PLL vs. Costas Loop:

The PLL described in this experiment is very similar to the Costas loop presented in coherent demodulation of DSBSC-AM. However, the bandwidth of the PLL used for FM demodulation must be large enough to pass the baseband message signal, while the Costas loop is used to generate a stable carrier reference signal so its bandwidth should be very small and just wide enough to track carrier drift and allow a reasonable acquisition time.