Frequency & Phase Modulation

FREQUENCY & PHASE MODULATION:

Besides using the amplitude of carrier to carrier information, one can also use the angle of a  carrier to carrier information. This approach is called angle modulation, and includes frequency modulation (FM) and phase modulation (PM). The amplitude of the carrier is maintained constant. The major advantage of this approach is that it allows the trade-off between bandwidth and noise performance.

An angle modulated signal can be written as

s t = Acosθ(t)

where θ(t) is usually of the form θ t = 2πfct + ∅(t) and fc is the carrier frequency. The signal ∅(t) is derived from the message signal m(t) . If ∅ t = kpm(t) for some constant kp ,the resulting  modulation  is  called  phase  modulation. The  parameter  kp is  called  the  phase sensitivity.In telecommunications and signal processing, frequency modulation (FM) is the encoding of information in a carrier wave by varying the instantaneous frequency of the wave. (Compare with amplitude modulation, in which the amplitude of the carrier wave varies, while the frequency remains constant.) Frequency modulation is known as phase modulation when the carrier phase modulation is the time integral of the FM signal.

deviation, which represents the maximum shift away from fc in one direction, assuming xm(t) is limited to the range ±1.

While most of the energy of the signal is contained within fc ± f , it can be shown by Fourier analysis that a wider range of frequencies is required to precisely represent an FM signal. The frequency spectrum of an actual FM signal has components extending infinitely, although their amplitude decreases and higher-order components are often neglected in practical design problems.

Sinusoidal baseband signal:

Mathematically, a baseband modulated signal may be approximated by a sinusoidal continuous wave signal with a frequency f_m.

The integral of such a signal is:

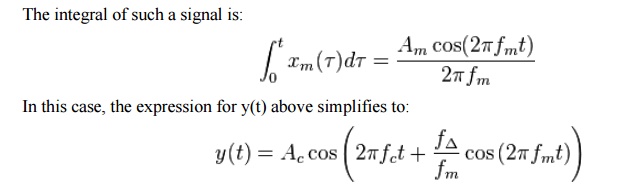
where the amplitude A_m of the modulating sinusoid is represented by the peak deviation fD

The harmonic distribution of a sine wave carrier modulated by such a sinusoidal signal can be represented with Bessel functions; this provides the basis for a mathematical understanding of frequency modulation in the frequency domain.

^ü Modulation index:

As in other modulation systems, the value of the modulation index indicates by how much the modulated variable varies around its unmodulated level. It relates to variations in the carrier frequency:

With a tone-modulated FM wave, if the modulation frequency is held constant and the modulation index is increased, the (non-negligible) bandwidth of the FM signal increases but the spacing between spectra remains the same; some spectral components decrease in strength as others increase. If the frequency deviation is held constant and the modulation frequency increased, the spacing between spectra increases.

Frequency modulation can be classified as narrowband if the change in the carrier frequency is about the same as the signal frequency, or as wideband if the change in the carrier frequency is much higher (modulation index >1) than the signal frequency. [6] For example, narrowband FM is used for two way radio systems such as Family Radio Service, in which the carrier is allowed to deviate only 2.5 kHz above and below the center frequency with speech signals of no more than 3.5 kHz bandwidth. Wideband FM is used for FM broadcasting, in which music and speech are transmitted with up to 75 kHz deviation from the center frequency and carry audio with up to a 20-kHz bandwidth.

Carson's rule:

BT = 2(Df+f_m)