Chapter: Transmission and Distribution : Modelling and Performance of Transmission Lines
Performance of Single Phase Short Transmission Lines
PERFORMANCE OF SINGLE PHASE SHORT TRANSMISSION LINES
As stated earlier, the effects of line capacitance are neglected for a short transmission line. Therefore, while studying the performance of such a line, only resistance and inductance of the line are taken into account. The equivalent circuit of a single phase short transmission line is shown in Fig.
Here, the total line resistance and inductance are shown as concentrated or lumped instead of being distributed. The circuit is a simple a.c. series circuit.
Let
I = load current
R = loop resistance i.e., resistance of both conductors
XL= loop reactance
VR = receiving end voltage
cos φR = receiving end power factor (lagging)
VS= sending end voltage
cos φS= sending end power factor

The *phasor diagram of the line for lagging load power factor is shown in Fig. From the right angled traingle ODC, we get,

An approximate expression for the sending end voltage Vs can be obtained as follows. Draw S perpendicular from B and C on OA produced as shown in Fig. Then OC is nearly equal to OF
OC = OF = OA + AF = OA + AG + GF
= OA + AG + BH
Vs= VR + IR cos φR + I XL sin φR
1. THREE-PHASE SHORT TRANSMISSION LINES
For reasons associated with economy, transmission of electric power is done by 3-phase system. This system may be regarded as consisting of three single phase units, each wire transmitting one-third of the total power. As a matter of convenience, we generally analyse 3-phase system by considering one phase only. Therefore, expression for regulation, efficiency etc. derived for a single phase line can also be applied to a 3-phase system. Since only one phase is considered, phase values of 3-phase system should be taken. Thus, Vs and VR are the phase voltages, whereas R and XL are the resistance S and inductive reactance per phase respectively.

Fig (i) shows a Y-connected generator supplying a balanced Y-connected load through a transmission line. Each conductor has a resistance of R Ω and inductive reactance of X Ω. Fig. ( ii) shows one phase separately. The calculations can now be made in the same way as for a single phase line.
2. Effect of Load p.f. On Regulation and Efficiency
The regulation and efficiency of a transmission line depend to a considerable extent upon the power factor of the load.
1. Effect on regulation.
The expression for voltage regulation of a short transmission line is given by :

The following conclusions can be drawn from the above expressions :
( i) When the load p.f. is lagging or unity or such leading that I R cos φR > I XL sin φR , then voltage regulation is positive i.e. , receiving end voltageVR will be less than the sending end voltage VS .
( ii) For a given VR and I, the voltage regulation of the line increases with the decrease in p.f. for lagging loads.
( iii) When the load p.f. is leading to this extent that I XL sin φR > I cos φ R , then voltage regulation is negative i.e. the receiving end voltage VR is more than the sending end voltage VS .
( iv) For a given VR and I, the voltage regulation of the line decreases with the decrease in p.f. for leading loads.
2. Effect on transmission efficiency.
The power delivered to the load depends upon the power factor.
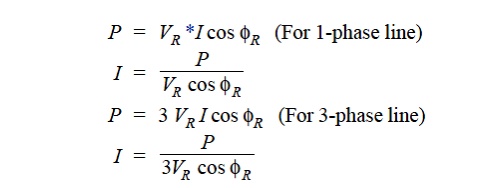
It is clear that in each case, for a given amount of power to be transmitted ( P) and receiving end voltage Power Factor Meter ( V R), the load current I is inversely proportional to the load p.f. cos φ R. Consequently, with the decrease in load p.f., the load current and hence the line losses are increased. This leads to the conclusion that transmission efficiency of a line decreases with the decrease in load Power Factor Regulator p.f. and vice-versa,
Related Topics