Chapter: Transmission and Distribution : Modelling and Performance of Transmission Lines
Medium Transmission Lines
MEDIUM TRANSMISSION LINES
In short transmission line calculations, the effects of the line capacitance are neglected because such lines have smaller lengths and transmit power at relatively low voltages (< 20 kV). However, as the length and voltage of the line increase, the capacitance gradually becomes of greater importance.
Since medium transmission lines have sufficient length (50-150 km) and usually operate at voltages greater than 20 kV, the effects of capacitance cannot be neglected. Therefore, in order to obtain reasonable accuracy in medium transmission line calculations, the line capacitance must be taken into consideration.
The capacitance is uniformly distributed over the entire length of the line. However, in order to make the calculations simple, the line capacitance is assumed to be lumped or concentrated in the form of capacitors shunted across the line at one or more points. Such a treatment of localising the line capacitance gives reasonably accurate results. The most commonly used methods (known as localised capacitance methods) for the solution of medium transmissions lines are :
( i) End condenser method
( ii) Nominal T method
( iii) Nominal π method.
Although the above methods are used for obtaining the performance calculations of medium lines, they can also be used for short lines if their line capacitance is given in a particular problem.
i)End Condenser Method
In this method, the capacitance of the line is lumped or concentrated at the receiving or load end as shown in Fig.This method of localising the line capacitance at the load end overestimates the effects of capacitance. In Fig, one phase of the 3-phase transmission line is shown as it is more convenient to work in phase instead of line-to-line values.
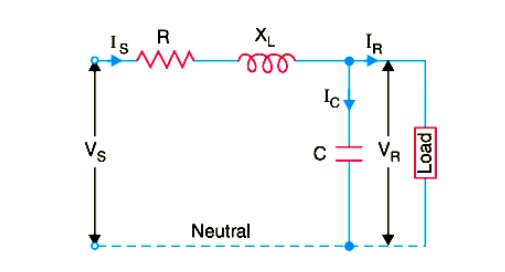
Let
I R= load current per phase R = resistance per phase
XL= inductive reactance per phase C = capacitance per phase
cos φR= receiving end power factor ( lagging) VS= sending end voltage per phase
The *phasor diagram for the circuit is shown in Fig Taking the receiving end voltage VR as the reference phasor,
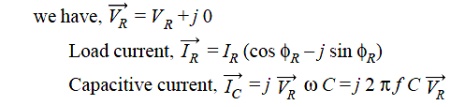
The sending end current Is is the phasor sum of load current IR and capacitive current IC i.e. ,

Limitations
Although end condenser method for the solution of medium lines is simple to work out calculations, yet it has the following drawbacks :
( i) There is a considerable error (about 10%) in calculations because the distributed capacitance has been assumed to be lumped or concentrated.
( ii) This method overestimates the effects of line capacitance.
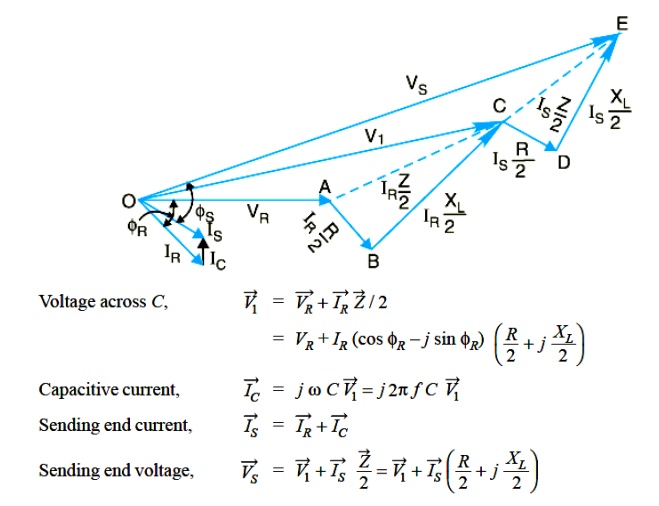
ii)Nominal T Method
In this method, the whole line capacitance is assumed to be concentrated at the middle point of the line and half the line resistance and reactance are lumped on its either side as shown in Fig.Therefore, in this arrangement, full charging current flows over half the line. In Fig. one phase of 3-phase transmission line is shown as it is advantageous to work in phase instead of line-to-line values.
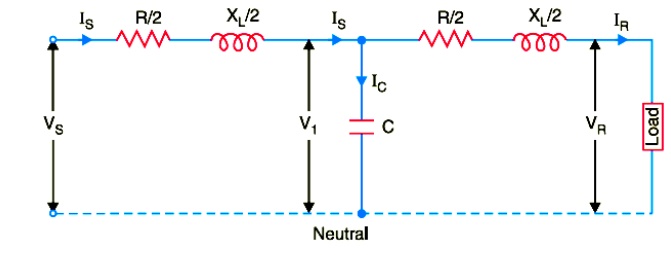
Let
IR = load current per phase ; R = resistance per phase
XL = inductive reactance per phase ; C = capacitance per phase
cos φR = receiving end power factor ( lagging) ; VS= sending end voltage/phase
V1 = voltage across capacitor C
The *phasor diagram for the circuit is shown in Fig. Taking the receiving end voltage VR as the reference phasor, we have,
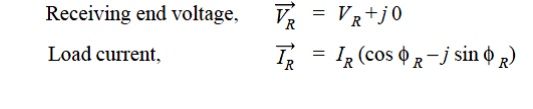
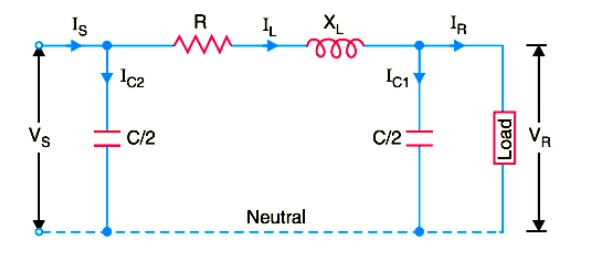
iii) Nominal π Method
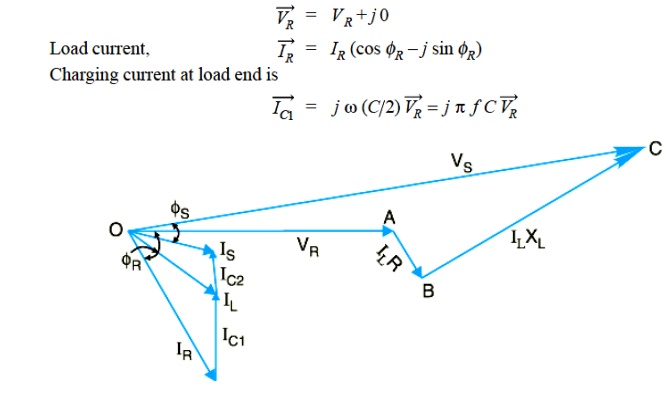
In this method, capacitance of each conductor ( i.e., line to neutral) is divided into two halves; one half being lumped at the sending end and the other half at the receiving end as shown in Fig. It is obvious that capacitance at the sending end has no effect on the line drop. However, its charging current must be added to line current in order to obtain the total sending end current.
Let
IR = load current per phase R = resistance per phase
XL = inductive reactance per phase C = capacitance per phase
cos φR = receiving end power factor ( lagging) VS= sending end voltage per phase
The *phasor diagram for the circuit is shown in Fig. Taking the receiving end voltage as the reference phasor, we have,
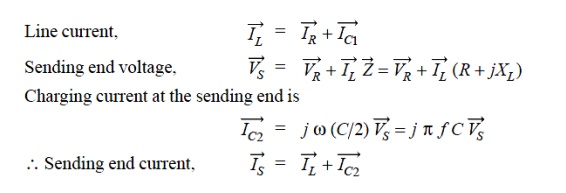
Related Topics