Chapter: Electrical machines : Synchronous Motors
Performance Characteristic of Synchronous Motors
Performance Characteristic
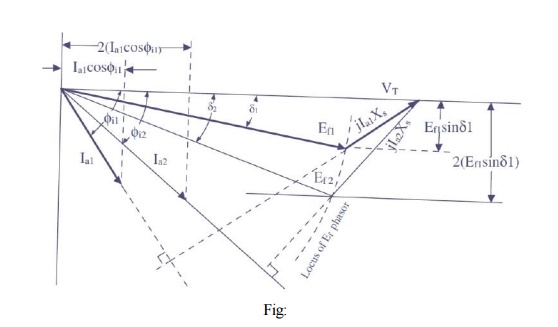
The effects of changes in mechanical or shaft load on armature current, power angle, and power factor can be seen from the phasor diagram shown in Fig: As the applied stator voltage, frequency, and field excitation are assumed, constant. The initial load conditions, are represented by the thick lines. The effect of increasing the shaft load to twice its initial value are represented by the light lines indicating the new steady state conditions. When the shaft load is doubled both Ia cos ϕi and Ef sinδ are doubled. While redrawing the phasor diagrams to show new steady-state conditions, the line of action of the new jIaXs phasor must be perpendicular to the new Ia phasor. Furthermore, as shown in Fig: if the excitation is not changed, increasing the shaft load causes the locus of the Ef phasor to follow a circular arc, thereby increasing its phase angle with increasing shaft load. Note also that an increase in shaft load is also accompanied by a decrease in ϕi ; resulting in an increase in power factor.
As additional load is placed on the machine, the rotor continues to increase its angle of lag relative to the rotating magnetic field, thereby increasing both the angle of lag of the counter EMF phasor and the magnitude of the stator current. It is interesting to note that during all this load variation, however, except for the duration of transient conditions whereby the rotor assumes a new position in relation to the rotating magnetic field, the average speed of the machine does not change. As the load is being increased, a final point is reached at which a further increase in δ fails to cause a corresponding increase in motor torque, and the rotor pulls out of synchronism. In fact as stated earlier, the rotor poles at this point, will fall behind the stator poles such that they now come under the influence of like poles and the force of attraction no longer exists. Thus, the point of maximum torque occurs at a power angle of approximately 90◦ for a cylindrical-rotor machine. This maximum value of torque that causes a synchronous motor to pull out of synchronism is called the pull-out torque. In actual practice, the motor will never be operated at power angles close to 90◦ as armature current will be many times its rated value at this load.
Effect of changes in field excitation on synchronous motor performance
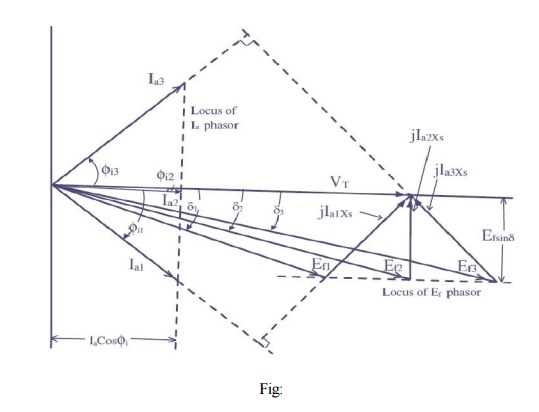
As increasing the strength of the magnets will increase the magnetic attraction, and thereby cause the rotor magnets to have a closer alignment with the corresponding opposite poles of the rotating magnetic poles of the stator. This will obviously result in a smaller power angle. When the shaft load is assumed to be constant, the steady-state value of Ef sinδ must also be constant. An increase in Ef will cause a transient increase in Ef sin , and the rotor will accelerate. As the rotor changes its angular position,δ decreases until Ef sinδ has the same steady-state value as before, at which time the rotor is again operating at synchronous speed, as it should run only at the synchronous speed. This change in angular position of the rotor magnets relative to the poles of rotating magnetic field of the stator occurs in a fraction of a second. The effect of changes in field excitation on armature current, power angle, and power factor of a synchronous motor operating with a constant shaft load, from a constant voltage, constant frequency supply, is illustrated in Fig:2.32. For a constant shaft load,
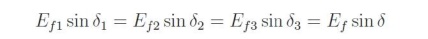
This is shown in Fig. 57, where the locus of the tip of the Ef phasor is a straight line parallel to the VT phasor. Similarly, for a constant shaft load,
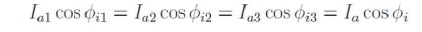
This is also shown in Fig. 57, where the locus of the tip of the Ia phasor is a line perpendicular to the VT phasor.
Note that increasing the excitation from Ef1 to Ef3 in Fig: caused the phase angle of the current phasor with respect to the terminal voltage VT (and hence the power factor) to go from lagging to leading. The value of field excitation that results in unity power factor is called normal excitation. Excitation greater than normal is called over excitation, and excitation less than normal is called under excitation. Furthermore, as indicated in Fig: 2.32, when operating in the overexcited mode, |Ef | > |VT |. In fact a synchronous motor operating under over excitation condition is sometimes called a synchronous condenser.
Power Factor Characteristic of Synchronous Motors
In an induction motor, only one winding (i.e., stator winding) produces the necessary flux in the machine. The stator winding must draw reactive power from the supply to set up the flux. Consequently, induction motor must operate at lagging power factor. But in a synchronous motor, there are two possible sources of excitation; alternating current in the stator or direct current in the rotor. The required flux may be produced either by stator or rotor or both.
(i) If the rotor exciting current is of such magnitude that it produces all the required flux, then no magnetizing current or reactive power is needed in the stator. As a result, the motor will operate at unity power factor.
(ii) If the rotor exciting current is less (i.e., motor is under-excited), the deficit in flux is made up by the stator. Consequently, the motor draws reactive power to provide for the remaining flux. Hence motor will operate at a lagging power factor.
If the rotor exciting current is greater (i.e., motor is over-excited), the excess flux must be counterbalanced in the stator. Now the stator, instead of absorbing reactive power, actually delivers reactive power to the 3-phase line. The motor then behaves like a source of reactive power, as if it were a capacitor. In other words, the motor operates at a leading power factor.
To sum up, a synchronous motor absorbs reactive power when it is under excited and delivers reactive power to source when it is over-excited.
Related Topics