Effect of Changing Field Excitation at Constant Load

Effect of Changing Field Excitation at Constant Load

In a d.c. motor, the armature current Ia is determined by dividing the difference between V and Eb by the armature resistance Ra. Similarly, in a synchronous motor, the stator current (Ia) is determined by dividing voltage-phasor resultant (Er) between V and Eb by the synchronous impedance Zs. One of the most important features of a synchronous motor is that by changing the field excitation, it can be made to operate from lagging to leading power factor. Consider a synchronous motor having a fixed supply voltage and driving a constant mechanical load. Since the mechanical load as well as the speed is constant, the power input to the motor (=3 V*Ia *cos ф) is also constant. This means that the in-phase component Ia cos ф drawn from the supply will remain constant. If the field excitation is changed, back e.m.f Eb also changes. This results in the change of phase position of Ia w.r.t. V and synchronous motor for different values of field excitation. Note that extremities of current phasor Ia lie on the straight line AB. hence the power factor cos   of the motor changes. Fig: shows the phasor diagram of the synchronous motor.

(i) Under excitation

The motor is said to be under-excited if the field excitation is such that Eb < V. Under such conditions, the current Ia lags behind V so that motor power factor is lagging as shown in Fig: (i). This can . be easily explained. Since Eb < V, the net voltage Er is decreased and turns clockwise. As angle ( δ δ = 90°) between Er and Ia is constant, therefore, phasor Ia also turns clockwise i.e., current Ia lags behind the supply voltage. Consequently, the motor has a lagging power factor.

(ii) Normal excitation

The motor is said to be normally excited if the field excitation is such that Eb = V. This is shown in Fig: 2.28 (ii). Note that the effect of increasing excitation (i.e., increasing Eb) is to turn the phasor Er and hence Ia in the anti-clockwise direction i.e., Ia phasor has come closer to phasor V. Therefore, p.f. increases though still lagging. Since input power (=3 V*Ia *cos ф) is unchanged, the stator current Ia must decrease with increase in p.f.

Suppose the field excitation is increased until the current Ia is in phase with the applied voltage V, making the p.f. of the synchronous motor unity [See Fig: 2.28 (iii)]. For a given load, at unity p.f. the resultant Er and, therefore, Ia are minimum.

 (iii) Over excitation 

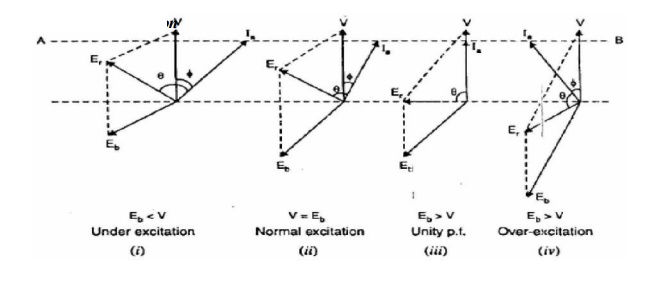
The motor is said to be overexcited if the field excitation is such that Eb > V. Under-such conditions, current Ia leads V and the motor power factor is leading as shown in Fig: 2.28 (iv). Note that Er and hence Ia further turn anti-clockwise from the normal excitation position. Consequently, Ia leads V. From the above discussion, it is concluded that if the synchronous motor is under-excited, it has a lagging power factor. As the excitation is increased, the power factor improves till it becomes unity at normal excitation. Under such conditions, the current drawn from the supply is minimum. If the excitation is further increased (i.e., over excitation), the motor power factor becomes leading. Note. The armature current (Ia) is minimum at unity p.f and increases as the power factor becomes poor, either leading or lagging.