Other Dependencies and Normal Forms

Other Dependencies and Normal Forms

We already introduced another type of dependency called join dependency (JD) in Section 15.7. It arises when a relation is decomposable into a set of projected relations that can be joined back to yield the original relation. After defining JD, we defined the fifth normal form based on it in Section 15.7. In the present section we will introduce some other types of dependencies that have been identified.

1. Inclusion Dependencies

Inclusion dependencies were defined in order to formalize two types of interrelational constraints:

        The foreign key (or referential integrity) constraint cannot be specified as a functional or multivalued dependency because it relates attributes across relations.

        The constraint between two relations that represent a class/subclass relation-ship (see Chapters 8 and 9) also has no formal definition in terms of the functional, multivalued, and join dependencies.

Definition. An inclusion dependency R.X < S.Y between two sets of attributes—X of relation schema R, and Y of relation schema S—specifies the constraint that, at any specific time when r is a relation state of R and s a relation state of S, we must have

π_X(r(R)) ⊆ π_Y(s(S))

The ⊆ (subset) relationship does not necessarily have to be a proper subset. Obviously, the sets of attributes on which the inclusion dependency is specified—X of R and Y of S—must have the same number of attributes. In addition, the domains for each pair of corresponding attributes should be compatible. For exam-ple, if X = {A₁, A₂, ..., A_n} and Y = {B₁, B₂, ..., B _n}, one possible correspondence is to have dom(A_i) compatible with dom(B_i) for 1 ≤ i ≤ n. In this case, we say that A_i corresponds to B_i.

For example, we can specify the following inclusion dependencies on the relational schema in Figure 15.1:

DEPARTMENT.Dmgr_ssn < EMPLOYEE.Ssn

WORKS_ON.Ssn < EMPLOYEE.Ssn

EMPLOYEE.Dnumber < DEPARTMENT.Dnumber

PROJECT.Dnum < DEPARTMENT.Dnumber

WORKS_ON.Pnumber < PROJECT.Pnumber

DEPT_LOCATIONS.Dnumber < DEPARTMENT.Dnumber

All the preceding inclusion dependencies represent referential integrity constraints. We can also use inclusion dependencies to represent class/subclass relationships. For example, in the relational schema of Figure 9.6, we can specify the following inclusion dependencies:

EMPLOYEE.Ssn < PERSON.Ssn

ALUMNUS.Ssn < PERSON.Ssn

STUDENT.Ssn < PERSON.Ssn

As with other types of dependencies, there are inclusion dependency inference rules (IDIRs). The following are three examples:

IDIR1 (reflexivity): R.X < R.X.

IDIR2 (attribute correspondence): If R.X < S.Y, where X = {A₁, A₂, ..., A_n} and

Y = {B₁, B₂, ..., B_n} and A_i corresponds to B_i, then R.A_i < S.B_i for 1 ≤ i ≤ n.

IDIR3 (transitivity): If R.X < S.Y and S.Y < T.Z, then R.X < T.Z.

The preceding inference rules were shown to be sound and complete for inclusion dependencies. So far, no normal forms have been developed based on inclusion dependencies.

 2. Template Dependencies

Template dependencies provide a technique for representing constraints in relations that typically have no easy and formal definitions. No matter how many types of dependencies we develop, some peculiar constraint may come up based on the semantics of attributes within relations that cannot be represented by any of them. The idea behind template dependencies is to specify a template—or example—that defines each constraint or dependency.

There are two types of templates: tuple-generating templates and constraint-generating templates. A template consists of a number of hypothesis tuples that are meant to show an example of the tuples that may appear in one or more relations. The other part of the template is the template conclusion. For tuple-generating templates, the conclusion is a set of tuples that must also exist in the relations if the hypothesis tuples are there. For constraint-generating templates, the template conclusion is a condition that must hold on the hypothesis tuples. Using constraint-generating templates, we are able to define semantic constraints—those that are beyond the scope of the relational model in terms of its data definition language and notation.

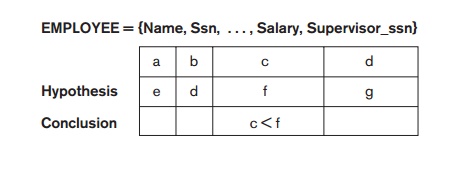
Figure 16.5 shows how we may define functional, multivalued, and inclusion dependencies by templates. Figure 16.6 shows how we may specify the constraint that an employee’s salary cannot be higher than the salary of his or her direct supervisor on the relation schema EMPLOYEE in Figure 3.5.

Figure 16.5

Templates for some common type of dependencies.

      Template for functional dependency X → Y.

      Template for the multivalued dependency X →→ Y.

Template for the inclusion dependency R.X < S.Y.

Figure 16.6

Templates for the constraint that an employee’s salary must be less than the supervisor’s salary.

3. Functional Dependencies Based on Arithmetic Functions and Procedures

Sometimes some attributes in a relation may be related via some arithmetic function or a more complicated functional relationship. As long as a unique value of Y is associated with every X, we can still consider that the FD X → Y exists. For example, in the relation

ORDER_LINE (Order#, Item#, Quantity, Unit_price, Extended_price,

Discounted_price)

each tuple represents an item from an order with a particular quantity, and the price per unit for that item. In this relation, (Quantity, Unit_price ) → Extended_price by the formula

Extended_price = Unit_price _* Quantity.

Hence, there is a unique value for Extended_price for every pair (Quantity, Unit_price ), and thus it conforms to the definition of functional dependency.

Moreover, there may be a procedure that takes into account the quantity discounts, the type of item, and so on and computes a discounted price for the total quantity ordered for that item. Therefore, we can say

(Item#, Quantity, Unit_price ) → Discounted_price, or (Item#, Quantity, Extended_price) → Discounted_price.

To check the above FD, a more complex procedure COMPUTE_TOTAL_PRICE may have to be called into play. Although the above kinds of FDs are technically present in most relations, they are not given particular attention during normalization.

4. Domain-Key Normal Form

There is no hard-and-fast rule about defining normal forms only up to 5NF. Historically, the process of normalization and the process of discovering undesirable dependencies were carried through 5NF, but it has been possible to define stricter normal forms that take into account additional types of dependencies and constraints. The idea behind domain-key normal form (DKNF) is to specify (theo-retically, at least) the ultimate normal form that takes into account all possible types of dependencies and constraints. A relation schema is said to be in DKNF if all constraints and dependencies that should hold on the valid relation states can be enforced simply by enforcing the domain constraints and key constraints on the relation. For a relation in DKNF, it becomes very straightforward to enforce all data-base constraints by simply checking that each attribute value in a tuple is of the appropriate domain and that every key constraint is enforced.

However, because of the difficulty of including complex constraints in a DKNF relation, its practical utility is limited, since it may be quite difficult to specify general integrity constraints. For example, consider a relation CAR(Make, Vin#) (where Vin# is the vehicle identification number) and another relation MANUFACTURE(Vin#, Country) (where Country is the country of manufacture). A general constraint may be of the following form: If the Make is either ‘Toyota’ or ‘Lexus,’ then the first character of the Vin# is a ‘J’ if the country of manufacture is ‘Japan’; if the Make is ‘Honda’ or ‘Acura,’ the second character of the Vin# is a ‘J’ if the country of manufacture is ‘Japan.’

There is no simplified way to represent such constraints short of writing a procedure (or general assertions) to test them. The procedure COMPUTE_TOTAL_PRICE above is an example of such procedures needed to enforce an appropriate integrity constraint.