Further Discussion of Multivalued Dependencies and 4NF

Further Discussion of Multivalued Dependencies and 4NF

We introduced and defined the concept of multivalued dependencies and used it to define the fourth normal form in Section 15.6. Now we revisit MVDs to make our treatment complete by stating the rules of inference on MVDs.

1. Inference Rules for Functional and Multivalued Dependencies

As with functional dependencies (FDs), inference rules for multivalued dependencies (MVDs) have been developed. It is better, though, to develop a unified frame-work that includes both FDs and MVDs so that both types of constraints can be considered together. The following inference rules IR1 through IR8 form a sound and complete set for inferring functional and multivalued dependencies from a given set of dependencies. Assume that all attributes are included in a universal rela-tion schema R = {A₁, A₂, ..., A_n} and that X, Y, Z, and W are subsets of R.

IR1 (reflexive rule for FDs): If X ⊇ Y, then X → Y.

IR2 (augmentation rule for FDs): {X → Y} |= XZ → YZ.

IR3 (transitive rule for FDs): {X → Y, Y → Z} |= X → Z.

IR4 (complementation rule for MVDs): {X →→ Y} |= {X →→ (R – (X ∪ Y))}.

IR5 (augmentation rule for MVDs): If X →→ Y and W ⊇ Z, then WX →→ YZ.

IR6 (transitive rule for MVDs): {X →→ Y, Y →→ Z} |= X →→ (Z – Y).

IR7 (replication rule for FD to MVD): {X → Y} |= X →→ Y.

IR8 (coalescence rule for FDs and MVDs): If X →→ Y and there exists W with the properties that (a) W ∩ Y is empty, (b) W → Z, and (c) Y ⊇ Z, then X → Z.

IR1 through IR3 are Armstrong’s inference rules for FDs alone. IR4 through IR6 are inference rules pertaining to MVDs only. IR7 and IR8 relate FDs and MVDs. In particular, IR7 says that a functional dependency is a special case of a multivalued dependency; that is, every FD is also an MVD because it satisfies the formal definition of an MVD. However, this equivalence has a catch: An FD X → Y is an MVD X →→ Y with the additional implicit restriction that at most one value of Y is associated with each value of X.¹⁰ Given a set F of functional and multivalued dependencies specified on R = {A₁, A₂, ..., A_n}, we can use IR1 through IR8 to infer the (complete) set of all dependencies (functional or multivalued) F⁺ that will hold in every relation state r of R that satisfies F. We again call F⁺ the closure of F.

2. Fourth Normal Form Revisited

We restate the definition of fourth normal form (4NF) from Section 15.6:

Definition. A relation schema R is in 4NF with respect to a set of dependencies F (that includes functional dependencies and multivalued dependencies) if, for every nontrivial multivalued dependency X →→ Y in F⁺, X is a superkey for R.

To illustrate the importance of 4NF, Figure 16.4(a) shows the EMP relation in Figure 15.15 with an additional employee, ‘Brown’, who has three dependents (‘Jim’, ‘Joan’, and ‘Bob’) and works on four different projects (‘W’, ‘X’, ‘Y’, and ‘Z’). There are 16 tuples in EMP in Figure 16.4(a). If we decompose EMP into EMP_PROJECTS and EMP_DEPENDENTS, as shown in Figure 16.4(b), we need to store a total of only 11 tuples in both relations. Not only would the decomposition save on storage, but the update anomalies associated with multivalued dependencies would also be avoided. For example, if ‘Brown’ starts working on a new additional project ‘P,’ we must insert three tuples in EMP—one for each dependent. If we forget to insert any one of those, the relation violates the MVD and becomes inconsistent in that it incorrectly implies a relationship between project and dependent.

If the relation has nontrivial MVDs, then insert, delete, and update operations on single tuples may cause additional tuples to be modified besides the one in question. If the update is handled incorrectly, the meaning of the relation may change. However, after normalization into 4NF, these update anomalies disappear. For

Figure 16.4

Decomposing a relation state of EMP that is not in 4NF. (a) EMP relation with additional tuples. (b) Two corresponding 4NF relations EMP_PROJECTS and EMP_DEPENDENTS.

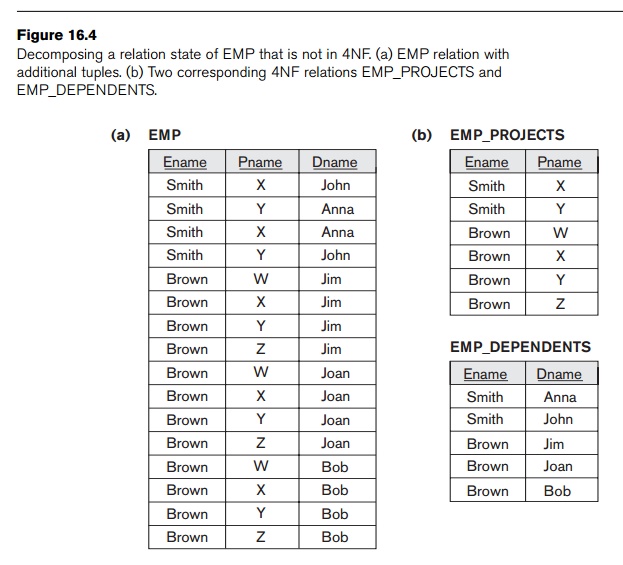
example, to add the information that ‘Brown’ will be assigned to project ‘P’, only a single tuple need be inserted in the 4NF relation EMP_PROJECTS.

The EMP relation in Figure 15.15(a) is not in 4NF because it represents two independent 1:N relationships—one between employees and the projects they work on and the other between employees and their dependents. We sometimes have a relationship among three entities that depends on all three participating entities, such as the SUPPLY relation shown in Figure 15.15(c). (Consider only the tuples in Figure 15.5(c) above the dashed line for now.) In this case a tuple represents a supplier supplying a specific part to a particular project, so there are no nontrivial MVDs. Hence, the SUPPLY all-key relation is already in 4NF and should not be decomposed.

3. Nonadditive Join Decomposition into 4NF Relations

Whenever we decompose a relation schema R into R₁ = (X ∪ Y) and R₂ = (R – Y) based on an MVD X →→ Y that holds in R, the decomposition has the nonadditive join property. It can be shown that this is a necessary and sufficient condition for decomposing a schema into two schemas that have the nonadditive join property, as given by Property NJB that is a further generalization of Property NJB given earlier. Property NJB dealt with FDs only, whereas NJB deals with both FDs and MVDs (recall that an FD is also an MVD).

Property NJB . The relation schemas R₁ and R₂ form a nonadditive join decomposition of R with respect to a set F of functional and multivalued dependencies if and only if

(R₁ ∩ R₂) →→ (R₁ – R₂)

or, by symmetry, if and only if (R₁ ∩ R₂) →→ (R₂ – R₁).

We can use a slight modification of Algorithm 16.5 to develop Algorithm 16.7, which creates a nonadditive join decomposition into relation schemas that are in 4NF (rather than in BCNF). As with Algorithm 16.5, Algorithm 16.7 does not necessarily produce a decomposition that preserves FDs.

Algorithm 16.7. Relational Decomposition into 4NF Relations with Nonadditive Join Property

Input: A universal relation R and a set of functional and multivalued depend-encies F.

        Set D:= { R };

        While there is a relation schema Q in D that is not in 4NF, do { choose a relation schema Q in D that is not in 4NF;

find a nontrivial MVD X →→ Y in Q that violates 4NF; replace Q in D by two relation schemas (Q – Y) and (X ∪ Y);

};