About Nulls, Dangling Tuples, and Alternative Relational Designs

About Nulls, Dangling Tuples, and Alternative Relational Designs

In this section we will discuss a few general issues related to problems that arise when relational design is not approached properly.

1. Problems with NULL Values and Dangling Tuples

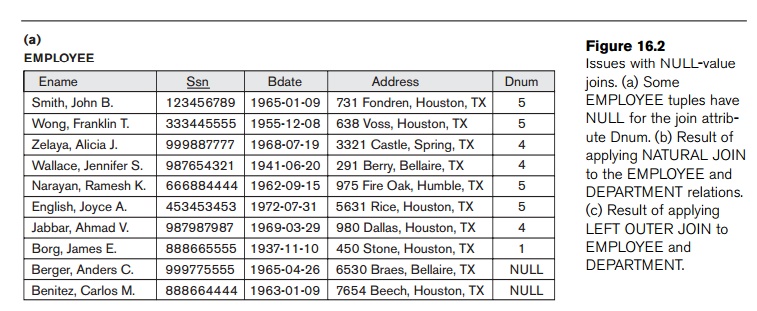
We must carefully consider the problems associated with NULLs when designing a relational database schema. There is no fully satisfactory relational design theory as yet that includes NULL values. One problem occurs when some tuples have NULL values for attributes that will be used to join individual relations in the decomposition. To illustrate this, consider the database shown in Figure 16.2(a), where two relations EMPLOYEE and DEPARTMENT are shown. 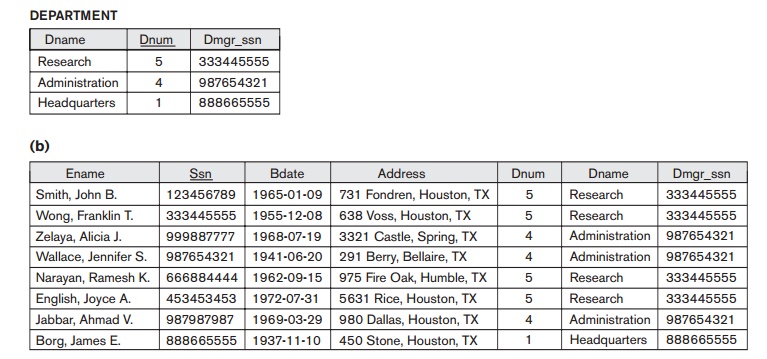The last two employee tuples— ‘Berger’ and ‘Benitez’—represent newly hired employees who have not yet been assigned to a department (assume that this does not violate any integrity constraints). Now suppose that we want to retrieve a list of (Ename, Dname) values for all the employees. 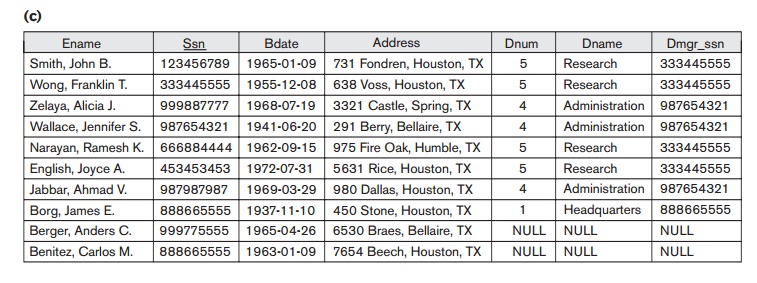If we apply the NATURAL JOIN operation on EMPLOYEE and DEPARTMENT (Figure 16.2(b)), the two aforementioned tuples will not appear in the result. The OUTER JOIN operation, discussed in Chapter 6, can deal with this problem. Recall that if we take the LEFT OUTER JOIN of EMPLOYEE with DEPARTMENT, tuples in EMPLOYEE that have NULL for the join attribute will still appear in the result, joined with an imaginary tuple in DEPARTMENT that has NULLs for all its attribute values. Figure 16.2(c) shows the result.

In general, whenever a relational database schema is designed in which two or more relations are interrelated via foreign keys, particular care must be devoted to watch-ing for potential NULL values in foreign keys. This can cause unexpected loss of information in queries that involve joins on that foreign key. Moreover, if NULLs occur in other attributes, such as Salary, their effect on built-in functions such as SUM and AVERAGE must be carefully evaluated.

A related problem is that of dangling tuples, which may occur if we carry a decomposition too far. Suppose that we decompose the EMPLOYEE relation in Figure 16.2(a) further into EMPLOYEE_1 and EMPLOYEE_2, shown in Figure 16.3(a) and 16.3(b). If we apply the NATURAL JOIN operation to EMPLOYEE_1 and EMPLOYEE_2, we get the original EMPLOYEE relation. However, we may use the alternative representation, shown in Figure 16.3(c), where we do not include a tuple

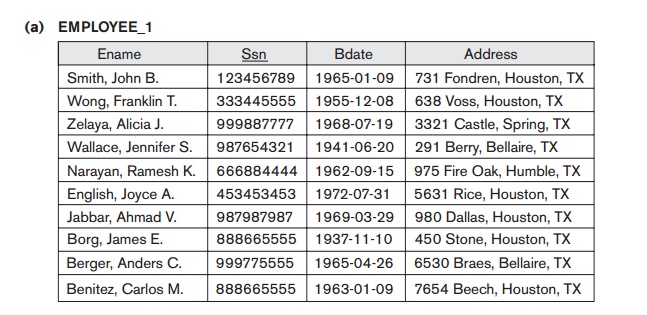
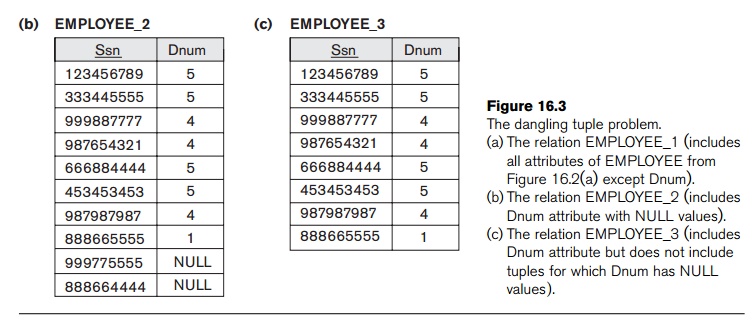
in EMPLOYEE_3 if the employee has not been assigned a department (instead of including a tuple with NULL for Dnum as in EMPLOYEE_2). If we use EMPLOYEE_3 instead of EMPLOYEE_2 and apply a NATURAL JOIN on EMPLOYEE_1 and

EMPLOYEE_3, the tuples for Berger and Benitez will not appear in the result; these are called dangling tuples in EMPLOYEE_1 because they are represented in only one of the two relations that represent employees, and hence are lost if we apply an (INNER) JOIN operation.

2. Discussion of Normalization Algorithms and Alternative Relational Designs

One of the problems with the normalization algorithms we described is that the database designer must first specify all the relevant functional dependencies among the database attributes. This is not a simple task for a large database with hundreds of attributes. Failure to specify one or two important dependencies may result in an undesirable design. Another problem is that these algorithms are not deterministic in general. For example, the synthesis algorithms (Algorithms 16.4 and 16.6) require the specification of a minimal cover G for the set of functional dependencies F. Because there may be in general many minimal covers corresponding to F, as we illustrated in Example 2 of Algorithm 16.6 above, the algorithm can give different designs depending on the particular minimal cover used. Some of these designs may not be desirable. The decomposition algorithm to achieve BCNF (Algorithm 16.5) depends on the order in which the functional dependencies are supplied to the algo-rithm to check for BCNF violation. Again, it is possible that many different designs may arise corresponding to the same set of functional dependencies, depending on the order in which such dependencies are considered for violation of BCNF. Some of the designs may be preferred, whereas others may be undesirable.

It is not always possible to find a decomposition into relation schemas that pre-serves dependencies and allows each relation schema in the decomposition to be in BCNF (instead of 3NF as in Algorithm 16.6). We can check the 3NF relation schemas in the decomposition individually to see whether each satisfies BCNF. If some relation schema R_i is not in BCNF, we can choose to decompose it further or to leave it as it is in 3NF (with some possible update anomalies).

To illustrate the above points, let us revisit the LOTS1A relation in Figure 15.13(a). It is a relation in 3NF, which is not in BCNF as was shown in Section 15.5. We also showed that starting with the functional dependencies (FD1, FD2, and FD5 in Figure 15.13(a)), using the bottom-up approach to design and applying Algorithm 16.6, it is possible to either come up with the LOTS1A relation as the 3NF design (which was called design X previously), or an alternate design Y which consists of three relations S₁, S₂, S₃ (design Y), each of which is a 3NF relation. Note that if we test design Y further for BCNF, each of S₁, S₂, and S₃ turn out to be individually in BCNF. The design X, however, when tested for BCNF, fails the test. It yields the two relations S₁ and S₃ by applying Algorithm 16.5 (because of the violating functional dependency A → C). Thus, the bottom-up design procedure of applying Algorithm 16.6 to design 3NF relations to achieve both properties and then applying Algorithm 16.5 to achieve BCNF with the nonadditive join property (and sacrificing functional dependency preservation) yields S₁, S₂, S₃ as the final BCNF design by one route (Y design route) and S₁, S₃ by the other route (X design route). This happens due to the multiple minimal covers for the original set of functional dependencies. Note that S₂ is a redundant relation in the Y design; however, it does not violate the nonadditive join constraint. It is easy to see that S₂ is a valid and meaningful relation that has the two candidate keys (L, C), and P placed side-by-side.

Table 16.1 summarizes the properties of the algorithms discussed in this chapter so far.