Number Systems

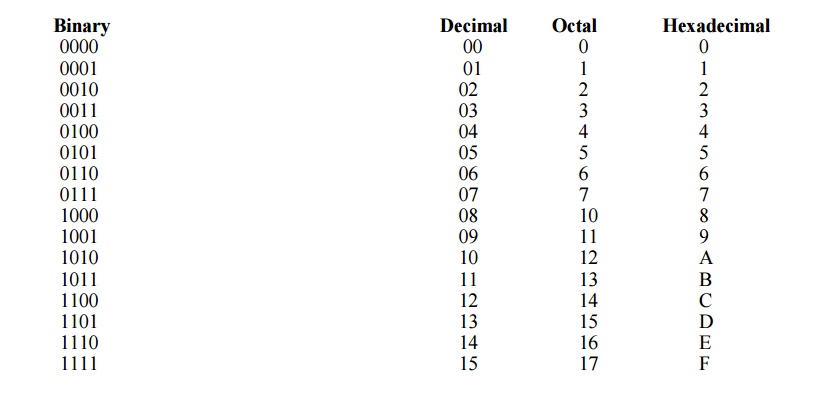
NUMBER SYSTEMS

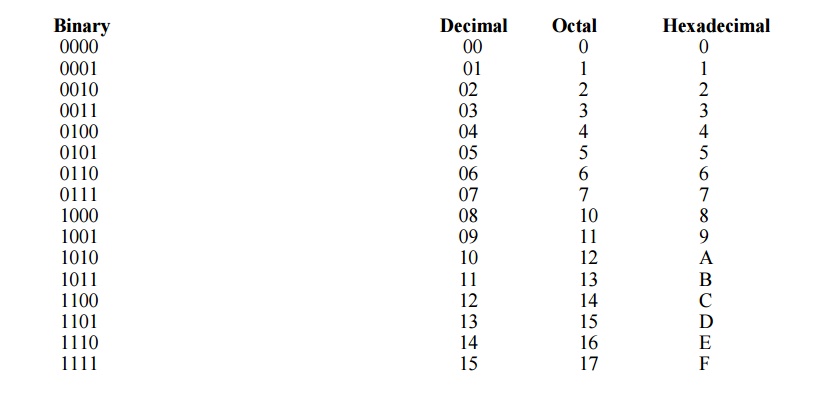
DECIMAL NUMBERS

In the decimal number systems each of the ten digits, 0 through 9, represents a certain quantity. The position of each digit in a decimal number indicates the magnitude of the quantity represented and can be assigned a weight. The weights for whole numbers are positive powers of ten that increases from right to left, beginning with 10º = 1 that is 10³ 10² 10¹ 10º

For fractional numbers, the weights are negative powers of ten that decrease from left to right beginningwith 10¯¹ that is 10² 10¹ 10º. 10¯¹ 10¯² 10¯³

The value of a decimal number is the sum of digits after each digit has been multiplied by its weights asin following examples

Express the decimal number 87 as a sum of the values of each digit.

The digit 8 has a weight of10 which is 10 as indicated by its position. The digit 7 has a weight of 1 which is 10º as indicated by its position.

87 = (8 x 10¹⁾ + (7 x 10⁰)

Express the decimal number 725.45 as a sum of the values of each digit.

725. 45 = (7 x 10²) + (2 x 10¹) + (5 x 10º) + (4 x 10¯¹) + (5 x 10¯²) = 700 + 20 + 5 + 0.4 + 0.05

BINARY NUMBERS

The binary system is less complicated than the decimal system because it has only two digits, it is a basetwo system. The two binary digits (bits) are 1 and 0. The position of a 1 or 0 in a binary number indicates its weight, or value within the number, just as the position of a decimal digit determines the value of that digit. The weights in a binary number are based on power of two as:

….. 2⁴ 2³ 2² 2¹ 2⁰. 2^-1 2^-2 ….

With 4 digits position we can count from zero to 15.In general, with n bits we can count up to a number equal to Ķ - 1. Largest decimal number = Ķ - 1.A binary number is a weighted number. The right-most bit is the least significant bit (LSB) in a binary whole number and has a weight of 2º =1. The weights increase from right to left by a power of two for each bit. The left-most bit is the most significant bit (MSB); its weight depends on the size of the binary number.

BINARY-TO-DECIMAL CONVERSION

The decimal value of any binary number can be found by adding the weights of all bits that are 1 and discarding the weights of all bits that are 0

Example

Let‘s convert the binary whole number 101101 to decimal

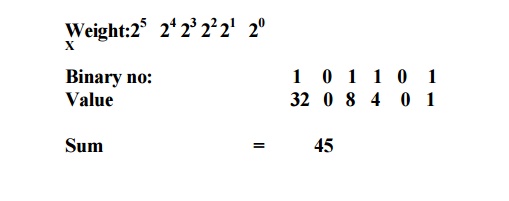
HEXADECIMAL NUMBERS

The hexadecimal number system has sixteen digits and is used primarily as a compact way of displaying or writing binary numbers because it is very easy to convert between binary and hexadecimal.Long binary numbers are difficult to read and write because it is easy to drop or transpose a bit. Hexadecimal is widely used in computer and microprocessor applications. The hexadecimal system has a base of sixteen; it is composed of 16 digits and alphabetic characters. The maximum 3-digits hexadecimal number is FFF or decimal 4095 and maximum 4-digit hexadecimal number is FFFF or decimal 65.535.

BINARY-TO-HEXADECIMAL CONVERSION

Simply break the binary number into 4-bit groups, starting at the right-most bit and replace each 4-bit group with the equivalent hexadecimal symbol as in the following example

Convert the binary number to hexadecimal: 1100101001010111 Solution:

1100  1010  0101  0111

C     A      5     7        = CA57

HEXADECIMAL-TO-DECIMAL CONVERSION

One way to find the decimal equivalent of a hexadecimal number is to first convert the hexadecimal number to binary and then convert from binary to decimal.

Convert the hexadecimal number 1C to decimal:

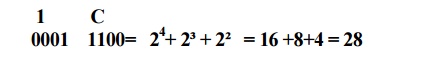
DECIMAL-TO-HEXADECIMAL CONVERSION

Repeated division of a decimal number by 16 will produce the equivalent hexadecimal number, formed by the remainders of the divisions. The first remainder produced is the least significant digit (LSD). Each successive division by 16 yields a remainder that becomes a digit in the equivalent hexadecimal number. When a quotient has a fractional part, the fractional part is multiplied by the divisor to get the remainder.

Convert the decimal number 650 to hexadecimal by repeated division by 16

650 /16 = 40.625  0.625 x 16 = 10    = A (LSD)

40 /16= 2.5 0.5 x 16 = 8 =      8

2/16= 0.125          0.125 x 16 = 2 =  2 (MSD)

The hexadecimal number is 28A             

OCTAL NUMBERS

Like the hexadecimal system, the octal system provides a convenient way to express binary numbers and codes. However, it is used less frequently than hexadecimal in conjunction with computers and microprocessors to express binary quantities for input and output purposes.

The octal system is composed of eight digits, which are: 0, 1, 2, 3, 4, 5, 6, 7

To count above 7, begin another column and start over: 10, 11, 12, 13, 14, 15, 16, 17, 20, 21 and so on. Counting in octal is similar to counting in decimal, except that the digits 8 and 9 are not used.

OCTAL-TO-DECIMAL CONVERSION

Since the octal number system has a base of eight, each successive digit position is an increasing power of eight, beginning in the right-most column with 8º. The evaluation of an octal number in terms of its decimal equivalent is accomplished by multiplying each digit by its weight and summing the products.

Let‘s convert octal number 2374 in decimal number.

Weight:       8³      8²      8¹ 8⁰

Octal number:      2        3        7  4

2374 = (2 x 8³) + (3 x 8²) + (7 x 8¹) + (4 x 8º) =1276

DECIMAL-TO-OCTAL CONVERSION

A method of converting a decimal number to an octal number is the repeated division-by-8 method, which is similar to the method used in the conversion of decimal numbers to binary or to hexadecimal.

Let‘s convert the decimal number 359 to octal. Each successive division by 8 yields a remainder that becomes a digit in the equivalent octal number. The first remainder generated is the least significant digit (LSD).

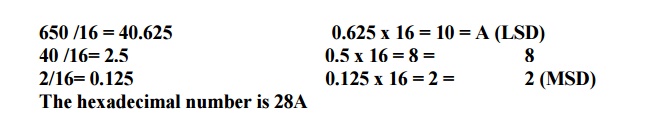
OCTAL-TO-BINARY CONVERSION

Because each octal digit can be represented by a 3-bit binary number, it is very easy to convert from octal to binary.

Octal/Binary Conversion

Octal Digit  0        1        2        3        4                 5        6        7

Binary        000    001    010    011    100    101    110    111

Let‘s convert the octal numbers 25 and 140.                                                      

Octal Digit  2        5        1        4        0

Binary                  010    101    001    100    000

BINARY-TO-OCTAL CONVERSION

Conversion of a binary number to an octal number is the reverse of the octal-to-binary conversion.

Let‘s convert the following binary numbers to octal:

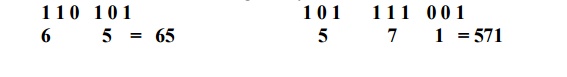
1 1 0  1 0 1  1 0 1  1 1 1  0 0 1

6        5  =  65       5        7        1  = 571