No load current - Design of Induction Motors

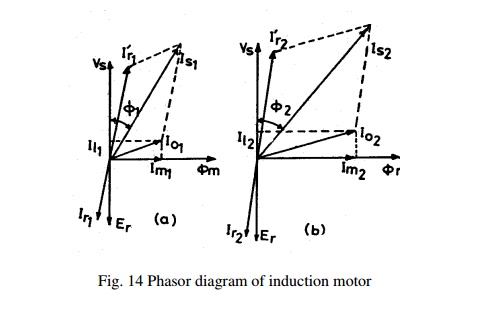
No load current: As seen from Fig 14, the no load current of an induction motor has two components magnetizing component, I_m and iron loss component, I_w. Phase relation between these currents is shown in Fig. 14.

Thus the no load current  I₀ = √(I_m)² + (I_w)² amps

Magnetising current: Magnetising current of an induction motor is responsible for producing the required amount of flux in the different parts of the machine. Hence this current can be calculated from all the magnetic circuit of the machine. The ampere turns for all the magnetic circuit such as stator core, stator teeth, air gap, rotor core and rotor teeth gives the total ampere turns required for the magnetic circuit. The details of the magnetic circuit calculations are studied in magnetic circuit calculations. Based on the total ampere turns of the magnetic circuit the magnetizing current can be calculated as

Magnetising current I_m= p AT₃₀ / (1.17 k_w T_ph )

where p – no of pairs of poles, AT₃₀ – Total ampere turns of the magnetic circuit at 30⁰ from the centre of the pole, T_ph – Number of stator turns per phase.

Iron loss component of current: This component of current is responsible for supplying the iron losses in the magnetic circuit. Hence this component can be calculated from no load losses and applied voltage.

Iron loss component of current  I_w= Total no load losses / ( 3 x phase voltage)

No load Power Factor: No load power factor of an induction motor is very poor. As the load on the machine increases the power factor improves. No load power factor can be calculated knowing the components of no load current.

No load power factor cosΦ₀ = I_w / I₀

Ex. While designing the stator of a 3 phase 10 kW, 400 volts, 50 Hz, 4 pole, wound rotor induction motor, following data are obtained.

Internal diameter of stator       = 0.19 m

Gross length         = 0.125 m

Number of stator slots   = 36

Number of conductors/slot      = 38

Dimension of stator slot          = 1.1 cm x 3.5 cm

Depth of the stator core = 3 cm

Number of rotor slots    = 30

Dimension of the rotor slot     = 0.7 cm x 3.0 cm

Depth of rotor core        = 3.0 cm

Carter’s coefficient for the air gap    = 1.33

Based on the above data, calculate the following performance data for this motor.

(i) Flux per pole  (ii) Iron losses  (iii) Active component of no load current (iv) No load current

(v) No load power factor

Soln.          (i) Flux per pole

Total number of stator conductors = 36 x 38 = 1368

Stator turns per phase T_ph = 1368 /6 = 228

Assuming star delta connection for the motor V_ph = 400 volts

Assuming  E_ph = V_ph = 400 volts, winding factor = 0.955

Air gap flux per pole  Φ = Eph/(4.44fT_ph k_w)

= 400/( 4.44 x 50 x 228 x 0.955)

= 0.00827 wb

(ii) Iron losses

Total Iron losses = Iron losses in stator teeth + Iron losses in stator core Iron losses in stator teeth:

For the given stator length assuming one ventilating duct of width 1cm and iron space factor of 0.95,

L_i = (L – n_d x w_d)k_i

=  (0.125 -1 x 0.01)0.95

= 0.109 m

Diameter at 1/3^rd height, D^' = D + 1/3 x h_ts x 2 = 0.19 + 1/3 x 0.035 x 2 = 0.213 m

Slot pitch at 1/3^rd height = τ^'_s = π x D^' /S_s = π x 0.213 /36 = 0.0186 m

Tooth width at this section = b^'_t = τ^'_s – b_s = 0.0186 – 0.011 = 0.0076 m

Area of the stator tooth per pole  A^'_t = b^'_t x l_i x number of teeth per pole

= b^'_t x l_i x S_s /p = 0.0076 x 0.109 x 36/4

= 0.00746 m²

Mean flux density in stator teeth  B'_t = Φ / A^'_t = 0.00827/ 0.00746 = 1.10 9 Tesla

Maximum flux density in stator tooth =1.5 x 1.109  = 1.66 Tesla

Volume of all the stator teeth = b^'_t x l_i x height of teeth x number of teeth

= 0.0076 x 0.109 x 0.035 x 36

= 0.001044 m³

Weight of all the teeth = volume x density Assuming a density of 7.8 x 10³ kg/ m³

Weight of all the teeth = 0.001044 x 7.8 x 10³ = 8.14 kg Total iron losses in the stator teeth = Total weight x loss/kg

Iron loss in the material at a flux density of 1.66 Tesla from graph PP-22 of DDH loss/kg = 23 w/kg

Total iron losses in the stator teeth = 23 x 8.14 = 187.22 watts

Iron losses in stator core : Sectional area of the stator core = l_i x d_c = 0.109 x 0.03 = 0.00327 m²

Mean diameter of the stator core below the slots = 0.19 + 2 x 0.035 + 0.03 = 0.29 m Volume of the stator core = π x D x Acs = π x 0.29 x 0.00327 = 0.002979 m³ Weight of the stator core = 0.002979 x 7.8 x 10³ = 23.23 kg

Flux density in stator core = Φ_c / Acs = 0.00827/(2 x 0.00327) = 1.264 Tesla At this flux density iron loss/kg = 17 watts/kg

Iron losses in the stator core = 17 x 23.23 = 394.91watts

Total iron losses in the stator = 187.22 + 394.91= 582.13 watts (iii) Active component of no load current

Assuming the friction and windage losses as 1% of output Friction and windage loss = 100 w Total no load losses = 582.13 + 100 = 682.13 watts

Active component of no load current = Iron loss component of current

I_w= Total no load losses / ( 3 x phase voltage) = 682.13/( 3 x 400) = 0.568 amps

(iv) Magnetising current: In order to calculate the magnetizing current ampere turns required for the various parts of the magnetic circuits are to be calculated.

(a)        Ampere turns for the stator core:

Pole pitch at he mean diameter of the stator core = π x D/ P = π x 0.29/ 4 = 0.23 m Length of the flux path in stator core = 1/3 x 0.23 = 0.077 m

Ampere turns per meter at a flux density of 1.264 Tesla from graph (PP-22 of DDH) 400

AT

Hence total ampere turns required for the stator core = 400 x 0.077 = 31

(b)       Ampere turns for the stator teeth:

Length of the flux path in stator teeth = 0.035m

Flux density in stator teeth at 30⁰ from the pole centre = 1.36 B_t^’

= 1.36 x 1.10 9 =1.508 Tesla Ampere turns per meter at a flux density of 1.508 Tesla (from graph PP-22 of DDH) is 1000 AT

Hence total ampere turns for the stator teeth = 1000 x 0.035 = 35

(c) Ampere turns for the air gap:

Length of the air gap = 0.2 + 2√DL = 0.2 + 2√0.19 x 0.125 = 0.51 mm Average flux density in the air gap = Φ/ (π x DL/ P) = 0.4696 Tesla

Carter’s coefficient for the air gap       = 1.33

Air gap flux density at 30⁰ from the centre of the pole B_g = 1.36 x Bav

= 1.36 x 0.4696 = 0.6387 Tesla

Hence Ampere turns for the air gap  = 796000B_gk_gl_g

AT_g = 796000 x 0.687 x 1.33 x 0.51 x 10^-3 = 371 AT

(d) Ampere turns for the rotor Teeth :

Diameter of the rotor =  D -2l_g =0.19 – 2 x 0.00051= 0.189 m

Diameter at 1/3^rd height form the narrow end of the teeth  D_r^’ = D – 2 x 2/3h_rs

= 0.189 – 4/3 x 0.03 = 0.149 m

Slot pitch at 1/3^rd height = τ^'_r = π x D_r^' /S_r = π x 0.149 /30 = 0.0156 m

Tooth width at this section = b^'_tr = τ^'_r – b_r = 0.0156 – 0.007 = 0.0086 m

Area of the stator tooth per pole A^'_tr = b^'_tr x l_i x number of teeth per pole

= 0.0086 x 0.107 x 30/4 = 0.0069 m²

Flux density in rotor teeth at 30⁰ from pole centre = 1.36 x 0.00827/0.0069 = 1.63 Tesla

Ampere turns/m at this flux density, from graph (PP-22 of DDH) = 2800

Length of flux path in rotor teeth = 0.03 m

Ampere turns for the rotor teeth 2800 x 0.03 = 84

(e) Ampere turns for the rotor core

Depth of the rotor core d_cr = 3 cm

Area of the rotor core A_cr = 0.03 x 0.107 = 0.00321 m²

Flux in the rotor =  ½ x 0.00827 = 0.004135 wb

Flux density in the rotor core = 0.004135/0.00321= 1.29 Tesla

Ampere turns/m at this flux density, from graph (PP-22 of DDH) = 380

Mean diameter of the rotor core = D_r – 2 x hr_s – d_cr = 0.189 – 2 x 0.03 – 0.03 = 0.099 m

Pole pitch at this section = π x 0.099 /4 = 0.078 m

Length of the flux path in rotor core = 1/3 x 0.078 = 0.026 m Total ampere turns for the rotor core = 380 x 0.026 =10

Total Ampere turns for the magnetic circuit = 31 + 35 + 371 + 84 +10 = 531 AT Magnetising current I_m = p(AT₃₀) / (1.17 x K_w x T_ph)

= 2 x 531 /( 1.17 x 0.955 x 228)

= 4.2 amps

(v) No load current

No load current per phase  I_o = √( I_w² + I_m²)

=   √( 0.56² + 4.2²)

= 4.24 amps

(vi)           No load power factor  cos  ₀ = I_w/I₀  = 0.56 /4.24 = 0.132