Narrow Band Noise

NARROW BAND NOISE:

1. Definition: A random process X(t) is bandpass or narrowband random process if its power spectral density SX(f) is nonzero only in a small neighborhood of some high frequency fc Deterministic signals: defined by its Fourier transform Random processes: defined by its power spectral density.

Notes:

1. Since X(t) is band pass, it has zero mean: E[(X(t)] = 0.

2. fc needs not be the center of the signal bandwidth, or in the signal bandwidth at all.

2. Narrowband Noise Representation:

In most communication systems, we are often dealing with band-pass filtering of signals. Wideband noise will be shaped into bandlimited noise. If the bandwidth of the bandlimited noise is relatively small compared to the carrier frequency, we refer to this as narrowband noise. We can derive the power spectral density Gn(f) and the auto-correlation function Rnn(τ) of the narrowband noise and use them to analyse the performance of linear systems. In practice, we often deal with mixing (multiplication), which is a non-linear operation, and the system analysis becomes difficult. In such a case, it is useful to express the narrowband noise as n(t) = x(t) cos 2πfct - y(t) sin 2πfct.

where fc is the carrier frequency within the band occupied by the noise. x(t) and y(t) are known as the quadrature components of the noise n(t). The Hibert transform of n(t) is n^ (t) = H[n(t)] = x(t) sin 2πfct + y(t) cos 2πfct.

·   Generation of quadrature components of n(t).

x(t) and y(t) have the following properties:

1. E[x(t) y(t)] = 0. x(t) and y(t) are uncorrelated with each other.

2. x(t) and y(t) have the same means and variances as n(t).

3. If n(t) is Gaussian, then x(t) and y(t) are also Gaussian.

4. x(t) and y(t) have identical power spectral densities, related to the power spectral density of n(t) by Gx(f) = Gy(f) = Gn(f- fc) + Gn(f+ fc) (28.5)

for fc - 0.5B < | f | < fc + 0.5B and B is the bandwidth of n(t).

3. Inphase and Quadrature Components:

In-Phase & Quadrature Sinusoidal Components

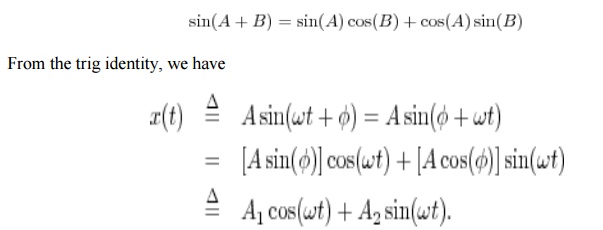
From this we may conclude that every sinusoid can be expressed as the sum of a sine function phase zero) and a cosine function (phase 2). If the sine part is called the ``in-phase'' component, the cosine part can be called the ``phase-quadrature'' component. In general, ``phase quadrature'' means ``90 degrees out of phase,'' i.e., a relative phase shift of ± 2. It is also the case that every sum of an in-phase and quadrature component can be expressed as a single sinusoid at some amplitude and phase. The proof is obtained by working the previous derivation backwards.Figure illustrates in-phase and quadrature components overlaid. Note that they only differ by a relative 00 degree phase shift.

·        Noise in AM receivers using Envelope detection:

In standard AM wave both sidebands and the carrier are transmitted. The AM wave may be written as s(t) = Ac[ 1+ kam(t) ] cos2πfct

The received signal x(t) at the envelope detector input consists of the modulated message signal s(t) and narrow band noise n(t). then,

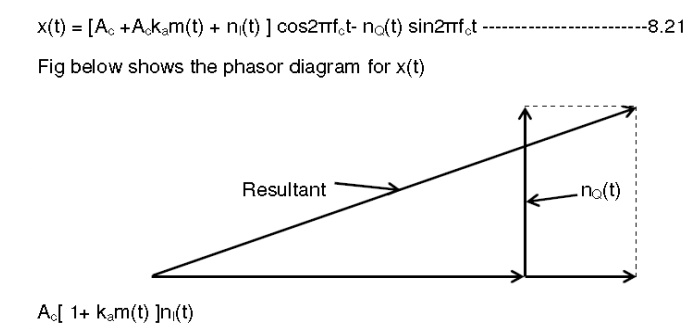
From this Phasor diagram for AM wave plus narrow-band noise for the case of high carrier –to-noise for the case of high carrier-to-noise ratio

From this phasor diagram the receiver output can be obtained as y(t) = envelope of x(t).

The average noise power is derived from both in-phase component and quadrature component,

.4 Signal to Noise Ratio:

FM NOISE REDUCTION: