Mode

Mode

As we have discussed earlier that the arithmetic mean is one of the form of representative value or measures of central tendency of a group of data. Depending upon the data and its purpose, other measures of central tendency may be used.

Consider the example of sale details of different sizes of footwear in a shop for a week.

The shopkeeper has to replenish his stock at the end of the week. Suppose we find the arithmetic mean of the footwear sold,

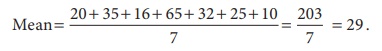
Mean= [ 20+35+16+65+32+25+10] / 7 = 203/7 = 29

Average number of footwear is 29. This means that the shopkeeper has to get 29 pairs of footwear in each size. Will it be wise to decide like this?

It has to be observed that the maximum purchase falls on the footwear of size 8 inches. So the shopkeeper has to get more number of footwear of size 8 inches. Hence arithmetic mean does not suit for this purpose. Here we need another type of representative value of data called ‘Mode’.

Mode is the value of the data which occurs maximum number of times.

Consider another example.

A shopkeeper analyses his sales data of readymade shirts to plan for the stock according to the demand. The sale details of shirts are given below.

Here he observes that there is a equal demand for shirts of sizes 30" and 34 " . Now this data has two modes as there are two maximum occurrences namely 30" and 34 " . He stocks more shirts of these 2 sizes. Note that, this data has two mode and it is known as bimodal data.

Try these

(1) Find the mode of the following data. 2,6,5,3,0,3,4,3,2,4,5,2

Solution:

Arranging the numbers in ascending order we get 0, 2, 2, 2, 3, 3, 3,4, 4, 5, 5, 6

Since 2 and 3 occurs the maximum of 3 times. So mode of this data is 2 and 3. 

(2) Find the mode of the following data set. 3, 12, 15, 3, 4, 12, 11, 3, 12, 9, 19

Solution:

Arranging the given data in ascending order : 3, 3, 3, 4, 9, 11, 12, 12, 12, 15, 19.

The data 3 and 12 occurs the maximum of 3 times.

So mode of this data is 3 and 12. 

(3) Find the mode of even numbers within 20.

Solution:

Even numbers within 20 arc 2, 4, 6, 8, 10, 12. 14. 16, 18.

There is no mode for this data. 

Example 5.5

Find the mode of the given set of numbers. 5, 7, 10, 12, 4, 5, 3, 10, 3, 4, 5, 7, 9, 10, 5, 12, 16, 20, 5

Solution:

Arranging the numbers in ascending order without leaving any value, we get, 3, 3, 4, 4, 5, 5, 5, 5, 5, 7, 7, 9, 10, 10, 10, 12, 12, 16, 20

Mode of this data is 5, because it occurs more number of times than the other values.

Note

To find mode, arranging the raw data in ascending order is not mandatory. It helps us to ensure that each and every value is taken into account for the calculation of mode and helps in identifying the mode value easily.

Example 5.6

The marks obtained by 11 students of a class in a test are 23, 2, 15, 38, 21, 19, 23, 23, 26, 34, 23. Find the mode of the marks.

Solution:

Arranging the given marks in ascending order, we get,

2, 15, 19, 21, 23, 23, 23, 23, 26, 34, 38.

Clearly, 23 occurs maximum number of times. Hence mode of marks=23.

Example 5.7

Find the mode of the following data 123, 132, 145, 176, 180, 120

Solution:

From the above data, we can see that there is no repetition of values in the given data. Each observation occurs only once, so there is no mode.

Note

When each of the observations have occurred only once, then there is no mode for the data.

Think

1. A toy factory making variety of toys for kids, wants to know the most popular toy liked by all the kids. Which average will be the most appropriate for it?

Solution:

Mode. 

2. Is there a mode exists between the odd numbers from 20 to 40? Discuss.

Solution: Odd number between 20 to 40 are 21, 23, 25, 27, 29, 31, 33, 35, 37, 39.

As all numbers occurs only once there is no mode for this data. 

1. Mode of large data

When size of the data is large, it is not easy to identify the value which occurs maximum number of times. In that case, we can group the data by using tally marks and then find the mode.

Consider the example to find the mode of the number of goals scored by a football team in 25 matches. The goal scored are 1, 3, 2, 5, 4, 6, 2, 2, 2, 4, 6, 4, 3, 2, 1, 1, 4, 5, 3, 2, 2, 4, 3, 0, 1.

To find the mode of this data, the number of goals score starting from 0 and ending with a maximum of 6 is represented in the form of a table.

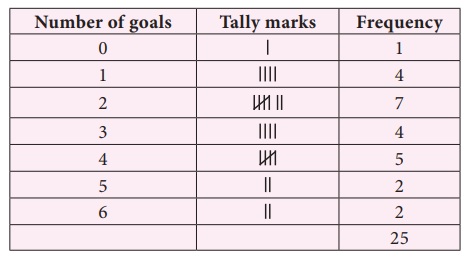
From the table we observe that the highest frequency is 7, which corresponds to number of goals, that is 2. Hence, the mode is 2.

Example 5.8

Find the mode of the following data. 14, 15, 12, 14, 16, 15, 17, 13, 16, 16, 15, 12, 16, 15, 13, 14, 15, 13, 15, 17, 15, 14, 18, 19, 12, 14, 15, 16, 15, 16, 13, 12.

Solution:

We tabulate the data as follows.

The whole data ranges from 12 to 19.

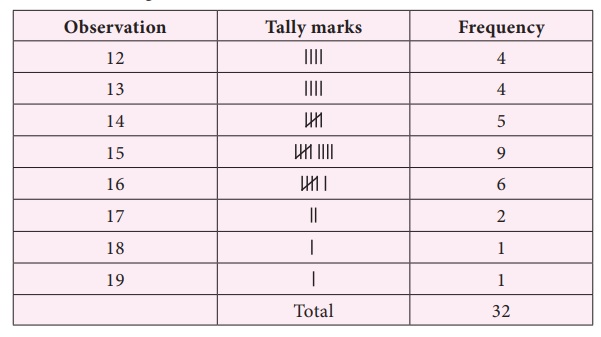
The highest frequency is 9 which corresponds to the value 15. Hence the mode of this data is 15.

Example 5.9

The following data shows that the number of hours spent by the students for study.

Find the mode.

Solution:

Since the one hour study time is spent by maximum number of students, the mode of the data is 1 hour.

Think

Which average will be most aprropriate for the companies producing the following goods? why?

(i) Diaries and notebooks (ii) School bags (iii) Jeans and T-shirts

Solution: For all the above data mode will be more appropriate.