Exercise 5.4

Exercise 5.4

Miscellaneous Practice problems

1. Arithmetic mean of 15 observations was calculated as 85. In doing so an observation was wrongly taken as 73 for 28. What would be correct mean?

Solution:

 Arithmetic mean = Sum of all observations / Number of observations

85 = Sum of 15 observation / 15

85 × 15 = sum of 15 observations

1275 = sum of 15 observations 

Wrong observation = 73

Correct observation = 28

∴ Correct Mean = [Sum – Wrong value + Correct value] / Number of obervation

= [1275 – 73 + 28] / 15 = [1202 + 28] / 15 = 1230 / 15 = 82

Correct Mean = 82

2. Find the median of 25, 16, 15, 10, 8, 30.

Solution:  

Arranging the data in ascending order: 8, 10, 15, 16, 25, 30

Here n = 6, even

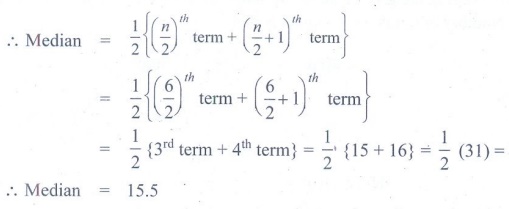
∴ Median = 1/2 {(n / 2)^th term + (n/2 + 1)^th term

= 1/2 {(6 / 2)^th term + (6/2 + 1)^th term

= 1/2 {3^th term + 4^th term}

= 1/2 {15 + 16} = 1/2 (31)

∴ Median = 15.5

3. Find the mode of 2, 5, 5, 1, 3, 2, 2, 1, 3, 5, 3.

Solution:  

Arranging the data in ascending order: 1, 1, 2, 2, 2, 3, 3, 3, 5, 5, 5

Here 2, 3 and 5 occurs 3 times each.

Which is the maximum number of times.

∴ Mode is 2, 3 and 5.

4. The marks scored by the students in social test out of 20 marks are as follows: 12, 10, 8, 18, 14, 16. Find the mean and median?

Solution:

Arranging the given data in ascending order: 8, 10, 12, 14, 16, 18.

Mean = Sum of all observations / Number of observations

= [ 8 +10 + 12 + 14 + 16 + 18 ] / 6 = 78 / 6

Mean = 13

There are n = 6 observations, which is even

∴ Median = 1/2 {(n / 2)^th term + (n/2 + 1)^th term

= 1/2 {(6/2)^th term + (6/2 + 1)^th term

= 1/2 {3^th term + 4^th term}

= 1/2 {8+18} = 1/2 (26) =13

∴ Median = 13 

5. The number of goals scored by a football team is given below. Find the mode and median for the data of 2, 3, 2, 4, 6, 1, 3, 2, 4, 1, 6.

Solution:

Arranging the given data in ascending order: 1, 1, 2, 2, 2, 3, 3, 4, 4, 6, 6

Clearly 2 occurs at the maximum of 3 times and so mode = 2

Here number of data of data n = 11, odd.

∴ Median = ([n + 1] / 2)^th term

= ([11+ 1] / 2)^th term = (12 / 2)^th term

= 6^th term

Median = 3

6. Find the mean and mode of 6, 11, 13, 12, 4, 2.

Solution:

Arranging is ascending order : 2, 4, 6, 11, 12, 13

Mean = Sum of all observations / Number of observations = [ 2 + 4 + 6 + 11 + 12 + 13] / 6

Mean = 48 / 6 = 8

All observation occurs only once and so there is no mode for this date.

Challenge Problems

7. The average marks of six students is 8. One more student mark is added and the mean is still 8. Find the student mark that has been added.

Solution:

Average = Sum of all observations / Number of observations

8 = Sum of observation / 6

Sum of observation = 6 × 8

 = 48

If one more mark is added then number of observations = 6 + 1 = 7

Let the number be x

Still average = 8

∴ 8 = [48 + x ] / 7

48 + x = 7 × 8

48 + x = 56

48 + x = 56 – 48

x = 8

∴ The number that is added = 8

8. Calculate the mean, mode and median for the following data: 22, 15, 10, 10, 24, 21.

Solution:

Arranging in ascending order: 10, 10, 15, 21, 22, 24

Mean = Sum of all observations / Number of observations

= [ 10 + 10 + 15 + 21 + 22 + 24 ] / 6

= 102 / 6 = 17

Here n = 6, even

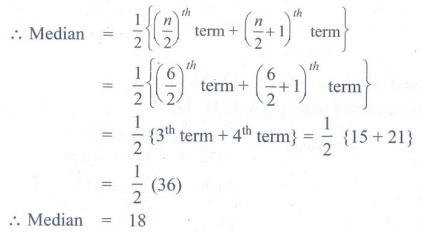
∴ Median = 1/2 {(n / 2)^th term + (n/2 + 1)^th term

= 1/2 {(6/2)^th term + (6/2 + 1)^th term

= 1/2 {3^th term + 4^th term}

= 1/2 {15 + 21} = 1/2 (36)

∴ Median = 18

Clearly the data 10 occurs maximum number of times and so 10 is the mode.

∴ Mode = 10

9. Find the median of the given data: 14, −3, 0, −2, −8, 13, −1, 7.

Solution:

Arranging in ascending order: –8, –3, –2, –1, 0, 7, 13, 14

Here number of data n = 8, even

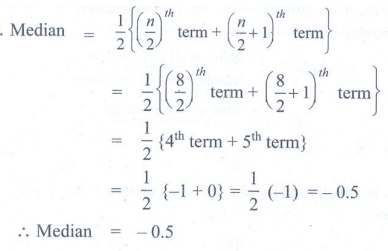
∴ Median = 1/2 {(n / 2)^th term + ([n/2] + 1)^th term

= 1/2 {(8 / 2)^th term + ([8/2] + 1)^th term

= 1/2 {4^th term + 5^th term}

= 1/2 {–1 + 0} = 1/2 (–1) = – 0.5

∴ Median = – 0.5

10. Find the mean of first 10 prime numbers and first 10 composite numbers.

Solution:

First 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29

Mean = Sum of all data / number of data

= [ 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 +29 ] / 10

= 129 / 10

Mean = 12.9

Mean of first 10 prime numbers = 12.9

First 10 prime numbers are 4, 6, 8, 9, 10, 12, 14, 15, 16, 18

Mean = [ 4 + 6 + 8 + 9 + 10 + 12 + 14 + 15 + 16 + 18 ] / 10

= 112 / 10

= 11.2

Mean of first 10 prime numbers = 11.2

ANSWERS:

 Exercise 5.4

1. 82

2. 15.5

3. 2, 3 and 5

4. 13;13

5. 2;3

6. 8; No mode.

 Challenge Problems

7. 8

8. 17; 10 ; 18

9. –0.5

10. 12.9 ; 11.2