Chapter: Digital Logic Circuits : Number Systems and Digital Logic Families
Min Terms and Max Terms
MIN TERMS AND MAX TERMS
Any boolean expression may be expressed in terms
of either minterms or maxterms. To do this we must first define the concept of
a literal. A literal is a single variable within a term which may or may not be
complemented. For an expression with N variables, minterms and maxterms are
defined as follows :
A minterm is the product of N distinct literals
where each literal occurs exactly once.
•
A maxterm
is the sum of N distinct literals where each literal occurs exactly once.
Product-of-Sums
Expressions
Standard
Forms
A product-of-sums expression contains the
product of different terms, with each term being either a single literal or a
sum of more than one literal. It can be obtained from the truth table by
considering those input combinations that produce a logic ‘0‘ at the output. Each such input combination gives a term, and the
product of all such terms gives the expression. Different terms are obtained by
taking the sum of the corresponding literals. Here, ‘0‘ and ‘1‘ respectively mean the uncomplemented and
complemented variables, unlike sum-of-products expressions where ‘0‘ and ‘1‘ respectively mean complemented and
uncomplemented variables.
Since each term in the case of the
product-of-sums expression is going to be the sum of literals, this implies
that it is going to be implemented using an OR operation. Now, an OR gate
produces a logic ‘0‘ only when all its inputs are in the logic ‘0‘ state, which means that the first term corresponding to the second row
of the truth table will be A+B+C. The product-of-sums Boolean expression for
this truth table is given by Transforming the given product-of-sums expression
into an equivalent sum-of-products expression is a straightforward process.
Multiplying out the given expression and carrying out the obvious
simplification provides the equivalent sum-of-products expression:
A given sum-of-products expression can be
transformed into an equivalent product-of-sums expression by (a) taking the
dual of the given expression, (b) multiplying out different terms to get the
sum-of products form, (c) removing redundancy and (d) taking a dual to get the
equivalent product-of-sums expression. As an illustration, let us find the
equivalent product-of-sums expression of the sum-of products expression
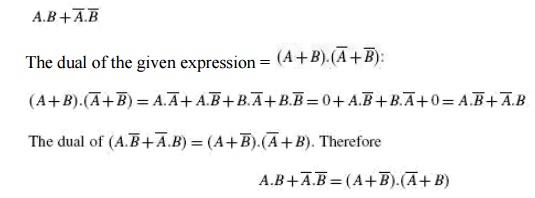
Related Topics