Measurement and kinetics of microbial growth

Measurement and kinetics of microbial growth

A clear understanding of microbial growth is necessary for proper utilization of biological processes for production of metabolites. In this section, the methods used for the measurement and quantitative evaluation of microbial growth will be discussed. There are four general patterns of microbial growth exemplified by bacteria, yeast, mold and viruses. All these microorganisms grow in different ways: bacteria grows by binary fission, yeast divide by budding, fungi divide by chain elongation and branching whereas viruses normally do not follow a regular growth pattern as they grow intracellularly in host cells.

Measurement of microbial growth

Microbial growth is defined as an orderly increase in all chemical components in the presence of suitable medium and environment. During the period of balanced growth, doubling of biomass is accompanied by doubling of other measurable properties of the microbe such as protein, DNA, RNA or intracellular water. In general, measurement of cell mass or cell number is used for quantitative measurement of cell growth. The parameter that characterises microbial growth is the doubling time. It is the time required for the cell mass or number to double its original value during the balanced growth (i.e., log phase) of the organism.

Measurement of cell mass or number is one of the easiest ways to measure microbial growth.

(1)          It is carried out by measuring the dry weight of the cell material in a fixed volume of the culture by removing the cells from the medium, and drying them till constant weight is obtained. For E. coli, the bacterium that is extensively used in laboratories, the dry cell weight of 1 billion cells is approximately 150 mg.

(2)          Cell growth is also measured by measuring the absorbance of cell suspensions in a spectrophotometer. This principle is based on the fact that small molecules scatter light proportionate to their concentration. When light passes through a suspension of bacteria, there is a reduction in light transmitted as a consequence of scattering. Thus, with different cell concentrations, the absorbance at a particular wavelength will be proportional to the cell concentration. If you have a standard graph, plotted with absorbance versus cell concentration, the cell concentration of the unknown microbial sample can be calculated by measuring the absorbance at the same wavelength.

Apart from the methods described above, other methods are also used for measuring cell growth. Some of these are: measurement of wet weight of cells, turbidity measurements, ATP measurement, viable plate count (colony forming units or cfu) and use of Coulter counter. Coulter counter is an electronic instrument and is used for direct counting of microbial cells in suspension. In Coulter counter, the cells are made to pass in a single file through electrical field and the electrical impedance thus generated is recorded.

Growth kinetics and specific growth rate

In order to understand microbial growth kinetics, we shall take bacterial binary fission as the example where each cell division produces two identical daughter cells. The time taken for the cell to divide is called generation time. The generation time is also known as doubling time (td), because the population of cells doubles over this time. For example, one cell of E.coli put in a nutritive medium will divide every 20 minutes. After one hour of growth (i.e. after three generations), one cell will have become eight (1 to 2, 2 to 4, 4 to 8). Because cell number doubles with each division, the increase in cell number over time is exponential or logarithmic.

A typical bacterial growth curve is depicted in Fig. 8. In the lag phase, the microbial population remains almost constant. It is however a period of intense metabolic activity as the bacteria adapt to the culture conditions. Once the cells have adapted to the culture, cell division occurs with increasing frequency until the maximum growth is reached. This is called the log phase. At this point exponential growth occurs and cell biomass or cell number increases at a constant rate.

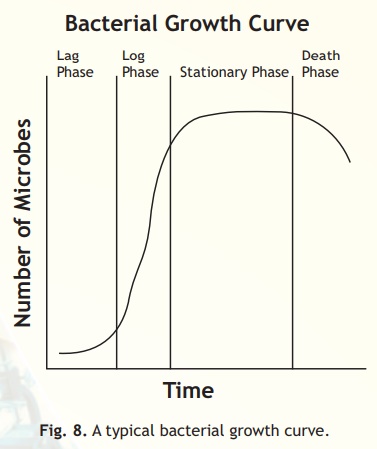
Fig. 8. A typical bacterial growth curve.

Mathematically, exponential growth can be described by two methods:

One related by biomass (X) and the other by cell numbers (N).

Let us first consider the exponential growth as related to biomass.

Balanced growth is like a chemical reaction where substrate is getting converted into product i.e. cell biomass in this case. Thus, growth behaves like an auto-catalytic reaction and the rate of growth will be proportional to the cell biomass present at that time. This can be described as follows:

rate of change of biomass dX / dt = µX

where

X      : concentration of biomass (g/L)

t       : time (h)

µ      : specific growth rate (hour -1)

The equation 1 can be rearranged to estimate the specific growth rate ( µ) as:

The specific growth rate µ = 1 / X . dX / dt                                   Eq.------- 2

Specific growth rate is an index of rate of growth of the cells in particular environment. In other words, specific growth rate is characteristic of the microorganism and is a function of the growth environment including temperature, pH, medium composition and levels of dissolved oxygen.

During the period of true exponential growth, equation 1 can be integrated to provide the following equation:

Xt = X0 eµt                                                                            Eq.   ------- 3

where

Xt : biomass conc. after time t

X0 : biomass conc. at the start of the exponential growth

e : base of the natural logarithm

Taking natural logarithm:

ln Xt = ln X0                      + µt    Eq.                                 -------- 4

This equation is of the form of straight-line y = mx + c.

Thus, for an exponentially growing culture, a plot of natural log of biomass concentration against time (i.e. a semilog plot) will give a straight line with the slope equal to µ.

or     µ = (ln Xt          —          ln X0) / t

Please note that if log10 values were plotted instead of natural log the slope would be equal to µ/2.303.

µ = 2.303 (Log Xt - LogX0) / t                                            Eq.     -------- 5

If we consider a situation where at time zero, the cell biomass is X0, then after exponential growth equivalent to one doubling time (td), the microbial biomass will become 2 X0.

i.e.  Xt  = 2X0       when t = td 

Substituting these parameters in Equation 3 gives:      

2X0  = X0 eµtd      Eq.----------- 6

Taking natural logarithm gives:

ln 2X0  = ln X0  + µtd

or     µtd  = ln 2

Thus,

td  = 0.693 / µ                                                                Eq.     ---------- 7

Where td is the doubling time of the culture.

By calculating µ from the graph or from Equation 5, and substituting it in Equation 7, we can calculate the doubling time of the culture. From the Equation 7, we can also say that doubling time and specific growth rates are inversely related. Higher the doubling time, lower will be the specific growth rate and vice versa. Thus, the microbial culture having high specific growth rate will have low doubling time.

Specific growth rate of microbial cells, in general, is calculated during the balanced growth of cells particularly during the exponential phase of growth. It signifies growth capacity of the culture in the particular environment. Specific growth rates of microbial cells change during different phases of batch growth, having a maximum value during the exponential phase. It is also affected by growth temperature, medium composition and other environmental parameters that affect the microbial growth.

Let us now study the second approach, which examines growth in relation to cell number, where number of the cells at the start of the exponential growth is N0.

Let us take an example where N0 = 1.

As the cell divides, we shall have:

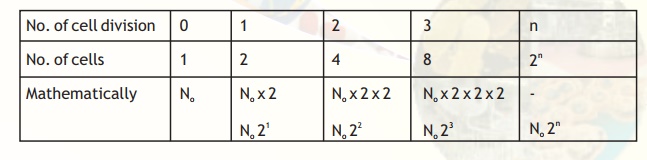
Thus, after a period of exponential growth time (t), the number of cells (Nt) will be given by:

N0 = the initial cell number

Taking logarithm

Log Nt  = Log N0  + n Log 2

Thus, the number of divisions (n) that have taken place is given by:

n = (Log Nt - Log N0 ) / Log 2

= (Log Nt - Log N0) / 0.301

= 3.3 (Log Nt - Log N0)                                                                Eq.-------- --- 9

The mean generation time or doubling time (td) i.e. the time taken to undergo single generation that doubles the population is:

td = Total growth time / number of divisions

= t / n                                                                                           Eq.---------- 10

The specific growth rate and doubling times of the organism decide the medium requirements and fermentation batch time for the production of biochemical molecules, and thus, are important parameters for large-scale production process.

Example: Calculate the generation time (doubling time or td) of a bacterial population in which the number of bacteria increases from 104/ml to 107/ml during four hours of exponential growth.

Answer: First calculate the number of divisions the population must have undergone to increase from 104 to 107 in 4 hours.

Using the equation 9:         n = 3.3 (Log 107 - Log 104)

=                3.3 (7 - 4)

=                10

Using the equation 10:       td = 240 minutes / 10

=                24 minutes