Matrices

Matrices

1. Matrices

‘Matrix’ is a singular while ‘matrices’ is a plural form. Matrix is a rectangular array of numbers systematically arranged in rows and columns within brackets. In a matrix, if the number of rows and columns are equal, it is called a square matrix.

2. Determinants

For every square matrix, there exists a determinant. This determinant is an arrangement of same elements of the corresponding matrix into rows and columns by enclosing vertical lines.

 is a determinant of the  matrix A denoted by A .

The value of the determinant is expressed as a single number.

Calculation of the value of determinant for a 2 x 2 matrix is shown below

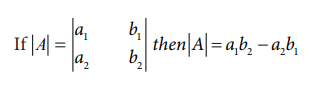
Calculation of determinant value for a 3 x 3 matrix is shown below

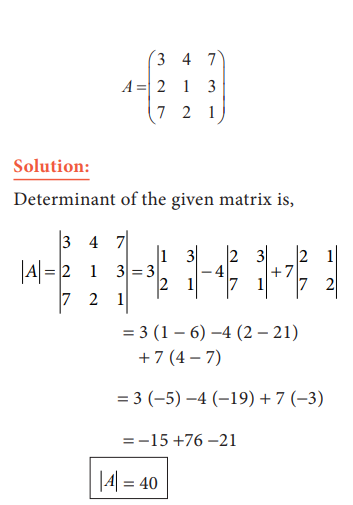
The value of determinant is 40.

3. Cramer’s Rule

Cramer’s rule provides the solution of a system of linear equations with ‘n’ variables and ‘n’ equations. It helpsto arrive at a unique solution of a system of linear equations with as many equations as unknowns.

a₁₁x + a₁₂ y + a₁₃ z = b₁

a₂₁x + a₂₂ y + a₂₃ z = b₂

a₃₁x + a₃₂ y + a₃₃ z = b₃

then

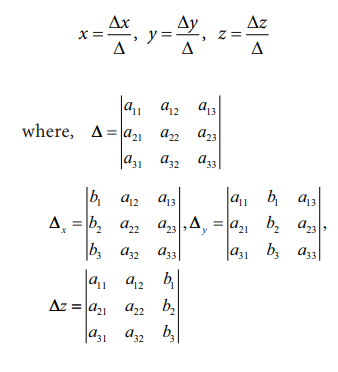
Example: 12.8

Find the value of x and y in the equations by using Cramer’s rule.

 x + 3y = 1 and

3x - 2y = 14

Then the equations in the matrix form :

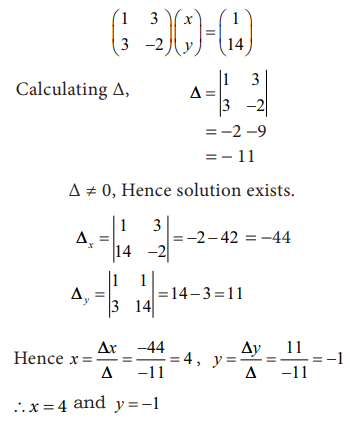
Key Note

If the determinant ∆=0 , then solution does not exist.

Answer checking:

Substituting in equation the values of x and y,

4+3(-1) = 1,

3(4) – 2(-1)= 14

Example: 12.9

Find the solution of the system of equations.

5x₁ + 3x₂ = 30

6x₁ - 2x₂ = 8

Solution:

The coefficient and the constant terms are given below for the equations

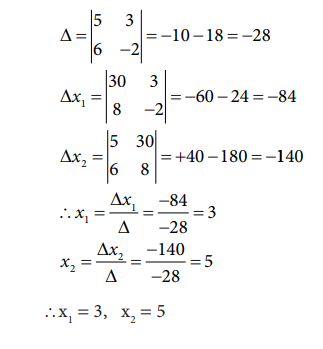
Example: 12.10

Find the solution of the equation system

7x₁ - x₂ - x₃ = 0

10x₁ - 2x₂ + x₃ = 8

6x₁ + 3x₂ - 2x₃ = 7

Solution:

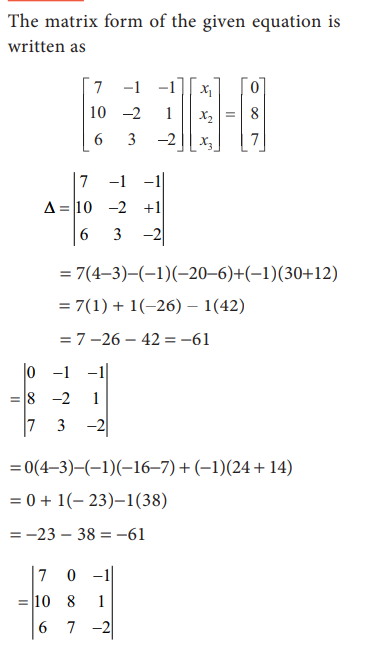
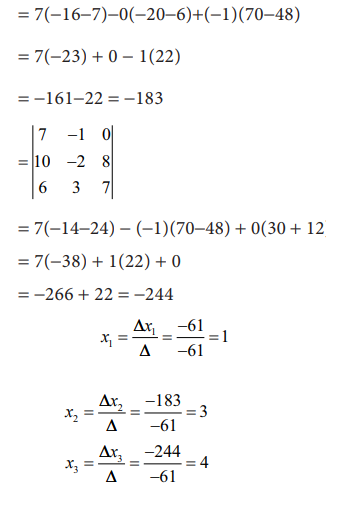
4. Application in Economics

Example 12.11

Mr.Anbu, purchased 2 pens, 3 pencils and 1 note book. Mr.Barakath , purchased 4 pens, 3 pencils and 2 notebooks. Mr.Charles purchased 2 pens, 5 pencils and 3 notebooks. They spent  Rs.32,  Rs.52 and  Rs.60 respectively. Find the price of a pen, a pencil and a note book.

Solution:

Let x be the price of a pen, y be the price of a pencil and z be the price of a notebook, In

equations:

2x + 3y + 1z = 32,

4x + 3y + 2z = 52,

2x + 5y +3z = 60

In matrix form

Answer checking

2(5)+3(4)+1(10)=32

4(5)+3(4)+2(10)=52

2(5)+5(4)+3(10)=60

Think and Do

Fathima, purchased 6 pens and 5 Pencils spending  Rs.49, Rani purchased 3 Pens and 4 pencils spending  Rs.32. What is the price of a pen and pencil? 

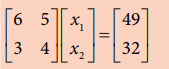
Solution : Price of a pen =  Rs.4 

Price of a pencil =  Rs.5