Integration, Meaning, Basic Rule, Formula, Solved Example Problems, Application | Economics - Integral Calculus | 11th Economics : Chapter 12 : Mathematical Methods for Economics
Chapter: 11th Economics : Chapter 12 : Mathematical Methods for Economics
Integral Calculus
Integral
Calculus
1. Integration
Differential
calculus measures the rate of change of functions. In Economics it is also
necessary to reverse the process of differentiation and find the function F(x)
whose rate of change has been given. This is called integration. The function
F(x) is termed an integral or anti- derivative of the function f(x).
The
integral of a function f(x) is expressed mathematically as
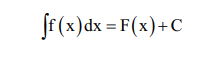
Here the
left hand side of the equation is read “the integral of f(x) with respect to x”
The symbol ∫ is an integral sign, f(x) is integrand, C is the constant of
integration, and F(x)+c is an
indefinite integral. It is so called because, as a function of x, which is here
unspecified, it can assume many values.
2. Meaning
If the
differential coefficient of F (x)
with respect to x is f(x), then an integral of f(x)
with
respect to x is F(x) . It is a reverse process of differentiation. In symbols:
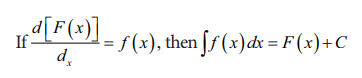
Following
points need to be remembered:
a. ∫ is used to denote the process of integration.
In fact, this symbol is an elongated ‘S’ denoting sum.
b. The
differential symbol ‘dx’ is written by the side of the function to be
integrated.
c. ∫ f x dx = F(x)+C, C is the integral constant
∫ f x dx means, integration of f(x) with
respect to x.
3. Basic Rule of Integration
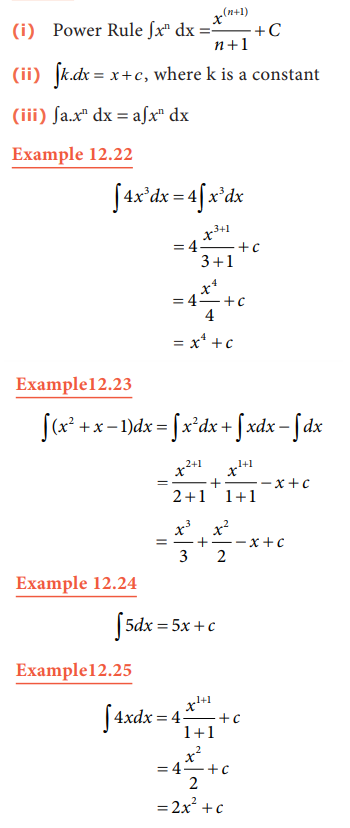
4. Application of Integration
Example 12.26
Let the
marginal cost function of a firm be 100-10x+0.1x2 where x is the output. Obtain the total cost function
of the firm under the assumption that its fixed cost is Rs.500.

Example 12.27
The
marginal cost function for producing x units is y = 23 + 16x - 3x2 and the total cost for producing zero unit is Rs.40.
Obtain the total cost function and the average cost function.
Solution:
Given the
marginal cost function y = 23 + 16x - 3x2 ; C = 40
Rs.40 is the
fixed cost.
We know
that
Total
Cost function = ∫ (Marginal cost function) dx+C
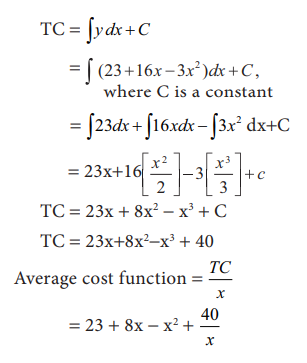
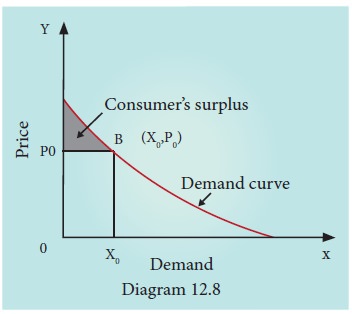
5. Consumer’s Surplus
This
theory was developed by the Alfred Marshall. The demand function P(x) reveals
the relationship between the quantities that the people would buy at given
price. It can be expressed as
P = f (x)
Consumer
surplus is the difference between the price one is willing to pay and the price
that is actually paid.
It is
represented in the following diagram.
Mathematically,
the consumer’s surplus (CS) can be defined as
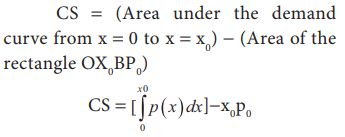
Example:12.28
If the
demand function is P = 35 - 2x - x2 and the demand x0
is 3, what will be the consumer’s surplus?
Solution
Given
demand function,
P = 35 - 2x - x2
for x = 3
= 35 - 2(3) -32
=35 - 6 - 9
P = 20
Therefore,
CS = (Area of the curve below the demand curve from 0 to 3) - Area of the rectangle (20 x 3 = 60)
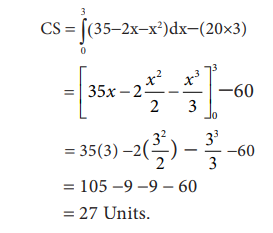
6. Producer’s surplus
Example 12.29
Given the
demand function Pd = 25 - Q2 and the supply function Ps = 2Q + 1.
Assuming
pure competition, find (a) consumers surplus and (b) producers surplus. (Pd
=Demand price; Ps = Supply
price)
Solution:
For
market equilibrium, Pd
= Ps
25-Q2 = 2Q+1
= -25 + Q2 + 2Q+1
0 = -24 + Q2 + 2Q
Q2
+ 2Q - 24 = 0
Q2 + 6Q - 4Q - 24 = 0
Q(Q + 6) -4(Q + 6) = 0
(Q + 6)(Q- 4) = 0
So, Q = 4 or Q = -6. Since
Q cannot be equal to -6,
Q = 4
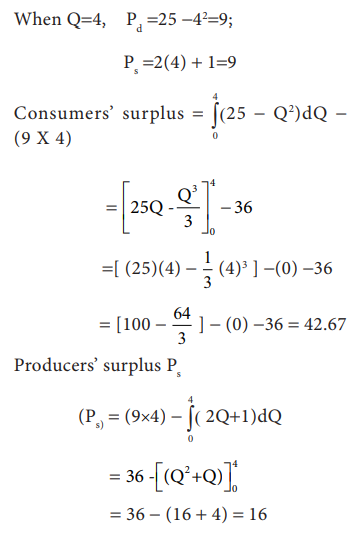
=36 - (16 + 4) = 16
Think
and Do
Find your change in mark by additional hour of study in any of
your subject
Find your consumption of petrol for an additional unit of
kilometer travelled
Ask your parents about their spending with respect to every
additional unit of wage or salary or income
Related Topics