Differential Calculus

DIFFERENTIAL CALCULUS

1. Meaning

The fundamental operation of calculus is differentiation. Derivative is used to express the rate of change in any function. Derivative means a change in the dependent variable with respect to small change (closer to zero) in independent variable.

Let the function be,

y = f(x)

Differentiating y with respect to x is,

2. Some Standard Forms of Differentiation

(Constant, addition and subtraction only)

3. Application of Differential Calculus

The relation between two or more variables can be expressed by means of a function. Continuous functions alone are differentiable. For instance, the differential calculus is applicable for finding the following:

1.        The rate of change in demand with respect to price (in micro economics)

2.        The rate of change in income with respect to the investment. (in macroeconomics) .

4. Marginal concepts

Marginal concept is concerned with variations of Y (on the margin of X), that is, it is the variation corresponding in Y to a very small variation in X. (X is the independent variable and Y is the dependent variable)

5. Marginal Product

Marginal product of a factor of production refers to addition to total product due to the use of an additional unit of a factor.

MP = d(TP)/dQ = ∆TP/∆Q

6. Marginal Cost

Marginal cost is an addition to the total cost caused by producing one more unit of output. In symbols:

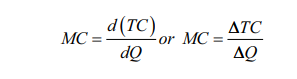
Where, ∆TC represents a change in total cost and ∆Q represents a small change in output or quantity. (in economics one worker, one output etc are assumed to be very small units)

Example: 12.17

Given the total cost function, TC = 15 + 3Q²+7Q³, drive the marginal cost function.

Solution:

TC = 15 + 3Q² + 7Q³

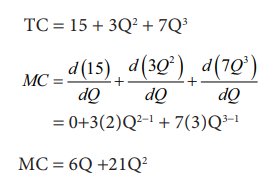
=0+3(2)Q2-1 + 7(3)Q3-1

MC = 6Q +21Q2

7. Marginal Revenue

Marginal Revenue is the revenue earned by selling an additional unit of the product. In other words, Marginal Revenue is an addition made to the total revenue by selling one more unit of the good.

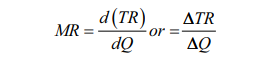
Where ∆TR stands for change in the total revenue, and ∆Q stands for change in output.

Example: 12.18

Given TR = 50Q - 4Q²,find marginal revenue when Q = 3.

Solution:

TR = 50Q - 4Q²

MR = d(TR)/dQ

MR = 50(1)Q^1-1 - 4(2)Q^2-1

=50(1)Q⁰ - 8 Q¹

=50(1) - 8Q (∴Q⁰ = 1,Q¹=Q)

MR = 50 - 8Q

When Q = 3

MR = 50 -8(3) =26

Example: 12.19

A producer has the total cost function TC (Q) = Q3 - 18Q2 + 91Q + 10 wherecosts are given in rupees. Find the marginal cost (MC) and the average variable cost (AVC), when Q =3.

Solution:

Given TC(Q) = Q3 - 18Q² + 91Q + 10, To find MC differentiate the function with respect to Q.

Example: 12.20

A manufacturer estimates that, when units of a commodity are produced each month the total costs will be TC(Q) = 128 + 60Q + 8Q² Find the marginal cost, average cost, fixed cost, variable cost, average fixed cost and average variable cost.

Solution:

Given that TC(Q) = 128 + 60Q + 8Q²

We know TC = Fixed cost + variable cost

 Average Variable cost =60 + 8Q (variable cost divided by Q)

∴AVC = 60 + 8Q

8. Elasticity of Demand

Elasticity of Demand is the ratio of the proportionate change in quantity demanded to the proportionate change in price. In mathematical terms,

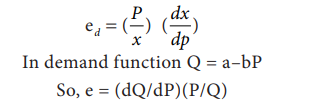
In demand function Q = a–bP

So, e = (dQ/dP)(P/Q)

Example 12.21