Chapter: Civil : Principles of Solid Mechanics : Concepts of Plasticity
Limit Load by a ÔÇťWorkÔÇŁ Calculation
Limit Load by a ÔÇťWorkÔÇŁ Calculation
The plastic collapse or limit load can be calculated
from equilibrium or by a work calculation based on an assumed mechanism of
collapse without first evaluating the elastic and plastic behavior of the
structure. For the thick ring it can be obtained directly from integrating the
equilibrium equation since at collapse
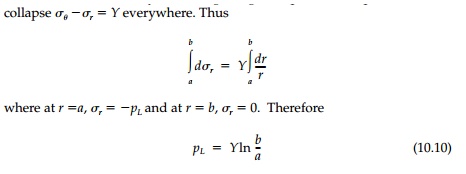
Computing this collapse load (without reference to
any partially elastic behavior leading to it) by equating internal to external
plastic work incre-ments is often easier and is quite different conceptually
since there is no need to consider stress distribution or even equilibrium.
This calculation can be thought of in terms of three steps:
1. Guess
a collapse mechanism, i.e., formulate the geometry of incre-mental deformation
of a plausible failure mechanism.
2. For
this incremental deformation, integrate the ÔÇťwork consumedÔÇŁ (i.e., energy) in
plastic deformation over the body.
3. Equate
this ÔÇťinternal plastic workÔÇŁ to the external work done by the limit load.
The first step is to describe the geometry of incremental
deformation so we can use the flow rule for plastic deformation increments
discussed in Section 10.1. For the thick ring:

is expressed in terms of the radial expansion of the
inner circumference, let c a u˙a
and
therefore

This is a state of pure shear deformation on planes
at 45o to the radius.
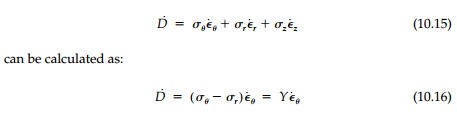
Thus the total dissipation of work per unit length
will be:
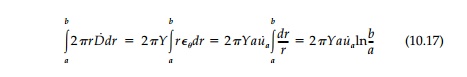
Finally, equating this
to the incremental external work done by pL as the ring
expands by u˙a
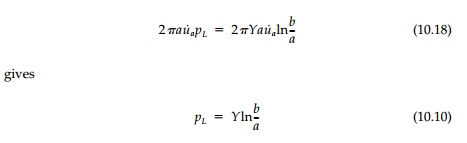
This is exactly the same result, but it is obtained
by considering only the geometry of the deformation of the collapse mechanism,
the normality rule, and the yield condition. In fact, no consideration of
equilibrium was neces-sary or, for that matter, was the distribution of stress
in the ring required.
Related Topics