Important Questions and Answers: Civil - Strength of Materials - Energy Principles

1.Define: Strain Energy

When an elastic body is under the action of external forces the body deforms and work is done by these forces. If a strained, perfectly elastic body is allowed to recover slowly to its unstrained state. It is capable of giving back all the work done by these external forces. This work done in straining such a body may be regarded as energy stored in a body and is called strain energy or resilience.

2. Define: Proof Resilience.

The maximum energy stored in the body within the elastic limit is called  Proof Resilience.

3. Write the formula to calculate the strain energy due to axial loads ( tension).

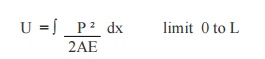
Where,

P = Applied tensile load.

L =  Length of the member

A = Area of the member

E = Young's modulus.

2.     Write the formula to calculate the strain energy due to bending.

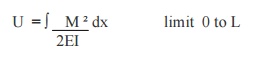
Where,

M = Bending moment due to applied loads.

E = Young's modulus

I = Moment of inertia

3.     Write the formula to calculate the strain energy due to torsion

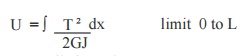
Where, T = Applied Torsion

G = Shear modulus or Modulus of rigidity

J = Polar moment of inertia

6.Write the formula to calculate the strain energy due to pure shear

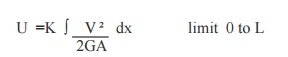
Where,

V= Shear load

G = Shear modulus or Modulus of rigidity

A = Area of cross section.

K = Constant depends upon shape of cross section.

7. Write down the formula to calculate the strain energy due to pure shear, if shear stress is given.

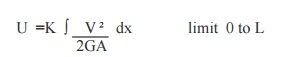
Where,   ? = Shear Stress

G = Shear modulus or Modulus of rigidity V = Volume of the material.

8. Write down the formula to calculate the strain energy , if the moment value is given

Where,   M = Bending moment

L = Length of the beam

E = Young's modulus

I = Moment of inertia

9. Write down the formula to calculate the strain energy , if the torsion moment value is given.

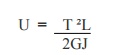
Where,    T = Applied Torsion

L = Length of the beam

G = Shear modulus or Modulus of rigidity J = Polar moment of inertia

10. Write down the formula to calculate the strain energy, if the applied tension load is given.

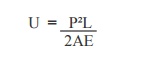
Where,

P = Applied tensile load. L = Length of the member

A = Area of the member

E = Young's modulus.

11. Write the Castigliano's first theorem.

In any beam or truss subjected to any load system, the deflection at any point is given by the partial differential coefficient of the total strain energy stored with respect to force acting at a point.

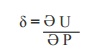
Where,

? = Deflection

U= Strain Energy stored

P = Load

12. What are uses of Castigliano's first theorem?

1. To determine the deflection of complicated structure.

2. To determine the deflection of curved beams springs.

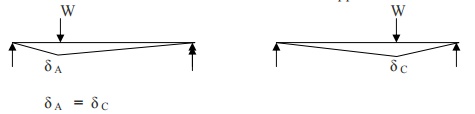
13.                                               Define: Maxwell Reciprocal Theorem.

In any beam or truss the deflection at any point 'A' due to a load 'W' at any other point 'C' is the same as the deflection at 'C' due to the same load 'W' applied at 'A'.

13.    Define: Unit load method.

The external load is removed and the unit load is applied at the point, where the deflection or rotation is to found.

15.                                               Give the procedure for unit load method.

1. Find the forces P1, P2, ……. in all the members due to external loads.

2.  Remove the external loads and apply the unit vertical point load at the joint if the

vertical deflection is required and find the stress.

3. Apply the equation for vertical and horizontal deflection.

16.                                               Compare the unit load method and Castigliano's first theorem

In the unit load method, one has to analyze the frame twice to find the load and deflection. While in the latter method, only one analysis is needed.

17.                        Find the strain energy per unit volume, the shear stress for a material is given as 50 N/mm ². Take G= 80000 N/mm ²

=  50 ² / (2 x 80000)

=  0.015625 N/mm ².  per unit volume.

18.Find the strain energy per unit volume, the tensile stress for a material is given as 150 N/mm ². Take E = 2 x10 N/mm ².

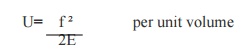
=  (150) ² / (2 x (2x10 ² )

=  0.05625 N/mm ².  per unit volume.

19.Define : Modulus of resilience.

The proof resilience of a body per unit volume. (ie) The maximum energy stored in the body within the elastic limit per unit volume.

20. Define : Trussed Beam.

A beam strengthened by providing ties and struts is known as Trussed Beams.

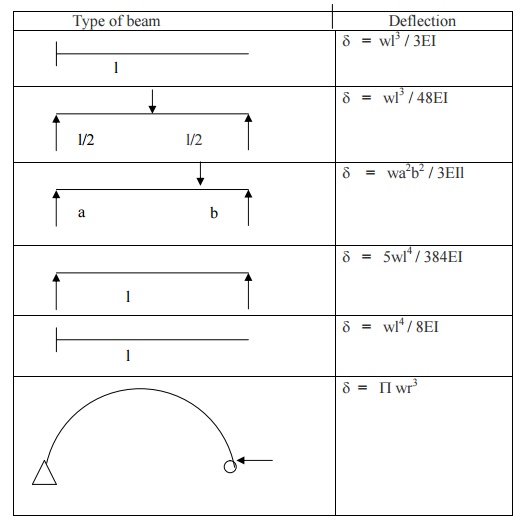
21. Deflection of beams