Chapter: Civil : Strength of Materials : Energy Principles
Energy Principles: Strain Energy, Proof Stress
STRAIN ENERGY
Whenever a body is strained, the energy is
absorbed in the body. The energy which is
absorbed in the body due to straining effect is known as strain energy.
The strain energy stored in the body is
equal to the work done by the applied load in stretching the body.
PROOF STRESS
The stress induced in an elastic body when it
possesses maximum strain energy is termed as
its proof stress.
Derive the expression for strain energy in
Linear Elastic Systems for the following cases. (i) Axial loading (ii) Flexural Loading (moment
(or) couple)
(i)Axial Loading
Let us
consider a straight bar of Length L, having uniform cross- sectional area A. If
an axial load P is applied gradually,
and one,ifstoredthe bar as strain energy
(U) in the body, will be equal to average force (1/2 P) multiplied by the deformation ?.
Thus U
= ½ P. ?
But
? = PL
/ AE
U
= ½ P. PL/AE = P2 L / 2AE
---------- (i)
If, however the bar has variable area of cross
section, consider a small of length dx and area
of cross section Ax. The strain energy dU stored in this small element
of length dx will be, from equation (i)
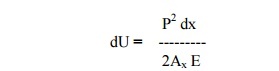
The total strain energy U can be obtained by
integrating the above expression over the length of the bar.
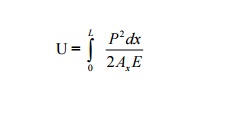
(ii) Flexural Loading (Moment or couple
)
Let us now consider a member of length L
subjected to uniform bending moment M.
Consider an element of length dx and let di be the change in
the slope of the element due to applied
moment M. If M is applied gradually, the strain energy stored in the small
element will be

(ii) Flexural Loading (Moment or couple )
Let us now consider a member of length L
subjected to uniform bending moment M.
Consider an element of length dx and let di be the change in
the slope of the element due to applied
moment M. If M is applied gradually, the strain energy stored in the small
element will be

Related Topics