Strength of Materials - Energy Principles

Energy Principles

Strain Energy, Proof Stress

 Whenever a body is strained, the energy is absorbed in the body. The energy which is  absorbed in the body due to straining effect is known as strain energy. The strain energy stored in the  body is equal to the work done by the applied load in stretching the body.

Proof Stress

 The stress induced in an elastic body when it possesses maximum strain energy is termed as  its proof stress.

 Derive the expression for strain energy in Linear Elastic Systems for the following cases. (i)  Axial loading (ii) Flexural Loading (moment (or) couple)

 (i)Axial Loading

 Let us consider a straight bar of Length L, having uniform cross- sectional area A. If an axial  load P is applied gradually, and one,ifstoredthe bar  as strain energy (U) in the body, will be equal to average force (1/2 P) multiplied by the  deformation ?.

Thus  U   =   ½   P.   ?  

 But   ?   =   PL   /   AE

 U = ½ P. PL/AE  = P² L / 2AE                                           ---------- (i)

 If, however the bar has variable area of cross section, consider a small of length dx and area  of cross section Ax. The strain energy dU stored in this small element of length dx will be,  from equation (i)

 The total strain energy U can be obtained by integrating the above expression over the length of the bar.

(ii) Flexural Loading (Moment or couple )

 Let us now consider a member of length L subjected to uniform bending moment M.  Consider an element of length dx and let d_i be the change in the slope of the element due to  applied moment M. If M is applied gradually, the strain energy stored in the small element will be

RESILIENCE

 The resilience is defined as the capacity of a strained body for doing work on the removal of  the straining force. The total strain energy stored in a body is commonly known as resilience.

PROOF RESILIENCE   

The proof resilience is defined as the quantity of strain energy stored in a body when strained   up to elastic limit. The maximum strain energy stored in a body is known as proof resilience.

MODULUS OF RESILIENCE

 It is defined as the proof resilience of a material per unit volume.

 Modulus of resilience =    Proof resilience /  Volume of the body

Two methods for analyzing the statically indeterminate structures.

 a. Displacement method (equilibrium method (or) stiffness coefficient method

 b.Force method (compatibility method (or) flexibility coefficient method)

Castigliano's   first   theorem   second   Theorem

 First Theorem.

 It states that the deflection caused by any external force is equal to the partial derivative of the  strain energy with respect to that force.

 Second Theorem

 It states that 'If U is the total strain ene  external force; its magnitude is always a minimum.

Castigliano's first   theorem:

 It states that the deflection caused by any external force is equal to the partial derivative  of the strain energy with respect to that force. A generalized statement of the theorem is as follows:

'  If   there   is   any umelastic under the action of system asetofaforcesin   equ

 W₁ , W₂, W₃ ………….W_n and   corresponding_1,?_2,?₃………….displacements?andset

 of moments M₁ , M₂, M₃………M_n  and   corresponding₁,₂,?₃,?……..rotations,then?

 the partial derivative of the total strain energy U with respect to any one of the forces or  moments taken individually would yield its corresponding displacements in its direction of  actions.'

 Expressed mathematically,

Proof:

 Consider an elastic body as show in fig subjected to loads W_1, W₂, W₃ ………etc.

 each applied independently. Let the body be supported at A, B etc. The reactions R_A ,R_B etc  do not work while the body deforms because the hinge reaction is fixed and cannot move  (and therefore the work done is zero) and the roller reaction is perpendicular to the displacements of the roller. Assuming that displacements of the points of loading will be linear functions of the loads and the principles of superposition will hold.

Let₁, ??2, ?3……… etc be the deflections of po loads at these points. The total strain energy U is then given by

 U = ½ (W₁?₁ + W₂ ?₂ +   ……….)---------  (iii)

 Let the load W₁ be increased by an amount dW_1, after the loads have been applied. Due to  this, there will be small changes in the deformation of the body, and the strain energy will be  increased slightly by an amount dU. expressing this small increase as the rate of change of U  with respect to W₁ times dW₁, the new strain energy will be

 On the assumption that the principle of superposition applies, the final strain energy does  not depend upon the order in which the forces are applied. Hence assuming that dW₁ is  acting on the body, prior to the application of W1_, W₂, W₃ ………etc, the deflection  infinitely small and the corresponding strain energy of the second order can be neglected.

 Now when W1_, W₂, W₃ ………etc,   are   applied ₁still actinginitially), (withthepointsdW1,  2, 3 etc will move through ₁ ,?  ?2,   ?3………   etc.   in   the   directio  energy will be given as above. Due to the application of W₁,   rides   through₁and   a  d produces the external work increment dU = dW₁ . ?₁. Hence the strain energy, when the loads  are applied is

 U+dW₁.₁?                                                                    ----------- (v)

 Since the final strain energy is by equating (iv) & (v).

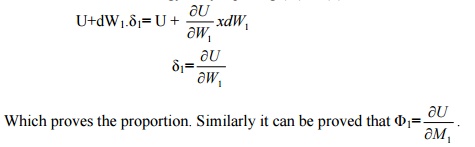
Deflection of beams by castigliano's first theo

 If a member carries an axial force the energies stored is given by

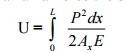
In the above expression, P is the axial force in the member and is the function of external  load W1, W2,W3 etc. To compute1 in the the direction of deflection W1

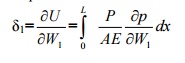
If the strain energy is due to bending and not due to axial load

 If no load is acting at the point where deflection is desired, fictitious load W is applied at the  point in the direction where the deflection is required. Then after differentiating but before  integrating the fictitious load is set to zero. This method is sometimes known as the fictitious  load method.₁ isIfrequiredthein directionrotationofM₁. ?

 Calculate the central deflection and the slope at ends of a simply supported beam carrying  a UDL w/ unit length over the whole span.

Solution:

 a) Central deflection:

 Since no point load is acting at the center where the deflection is required, apply the  fictitious load W, then the reaction at A and

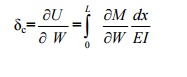
 Consider a section at a distance x from A.

 Bending moment at x,

 b) Slope at ends

 To obtain the slope at the end A, say apply a frictions moment A as shown in fig. The reactions at A and B will be

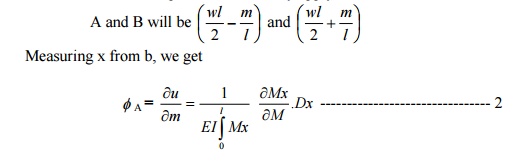
 Where Mx is the moment at a point distant x from the origin (ie, B) is a function of M.

Castigliano's second theorem:

It states that the strain energy of a linearly elastic system that is initially unstrained will have less strain energy stored in it when subjected to a total load system than it would have if it were self-strained.

 For example, if lis small strain (or) displacement, within the elastic limit in the direction of  the redundant force T,

 ?=0 when the redundant supports do not yield (or) when there is no initial lack of fit in the  redundant members.

Proof:

 Consider a redundant frame as shown in fig.in which Fc is a redundant member of  geometrical length L.Let the actual length of the member Fc be (L- ?), ? being the initial lack  of fit.F2 C represents thus the actual length (L- ?) of the member. When it is fitted to the truss,  the member will have to be pulled such that F2 and F coincide.

According   to   Hooke?s   law

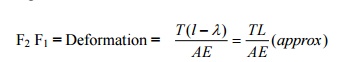
 Where T is the force (tensile) induced in the member.

 Hence FF₁=FF₂-F₁ F₂

 Let the member Fc be removed and consider a tensile force T applied at the corners F and C.

 FF₁ = relative deflection of F and C

 According to castigliano?s is the strain energy first of the whole theorem frame except wher  that of the member Fc.

Equating (i) and (ii) we get

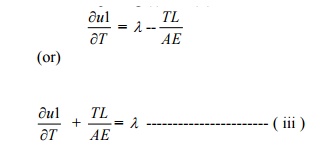
 To strain energy stored in the member Fc due to a force T is

Note:

i)                                                                            Castigliano?s theorem ofthe for analysisminimumofstatically strai  indeterminate beam ands portal tranes,if the degree of redundancy is not more than two.

ii)                                                           If the degree of redundancy is more than two, the slope deflection method or the moment  distribution method is more convenient.

 A beam AB of span 3mis fixed at both the ends and carries a point load of 9 KN at C distant 1m  from A. The M.O.I. of the portion AC of the beam is 2I and that of portion CB is I. calculate the  fixed end moments and reactions.

Solution:

 There are four unknowns M_a, Ra_, M_b and R_b.Only two equations of static are available  (ie) åv =0 and åM =0

 This problem is of second degree indeterminacy.

 First choose M_A and M_B as redundant.

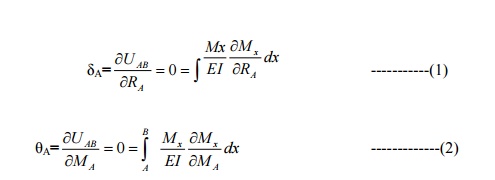
 1) For portion AC:

 Taking A as the origin

 M_x = -M_A + R_A x

 To find M_B, take moments at B, and apply the condition åM =0 there. Taking clockwise  moment as positive and anticlockwise moment as negative. Taking M_B clockwise, we have

 M_B -M_A =R_A (3) -9x2 = 0

 M_B -4.8 + (7.05x 3) -18 = 0

 M_B = 1.65 KN -m (assumed direction is correct)

 To find RB Apply  åV =0 for the whole frame.

 R_B = 9 -R_A = 9-7.05 = 1.95 KN

 Using Castigliano's First Theorem,rotationofthe determine  overhanging end A of the beam loaded.

Sol:

 Rotation of A:

 R_B x L = -M

 R_B = -M/L

 R_B = M/L ( ¯)

 & R_C = M/L ( ­)

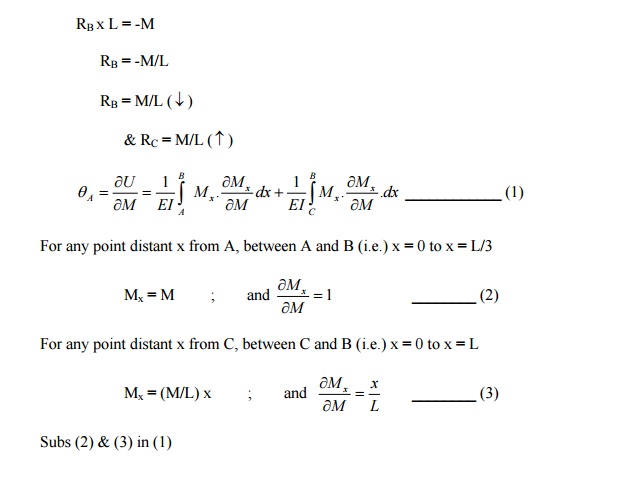
 b) Deflection of A:

 To find the deflection at A, apply a fictitious load W at A, in upward direction as

 shown in fig.

PRINCIPLE OF VIRTUAL WORK

 It states that the workdone on a structure by external loads is equal to the internal energy  stored in a structure (Ue = U_i)

 Work of external loads = work of internal loads

STRAIN ENERGY STORED IN A ROD OF LENGTH L AND AXIAL RIGIDITY AE TO  AN AXIAL FORCE P

 Strain energy stored

U=  P² L / 2AE

STATE THE VARIOUS METHODS FOR COMPUTING THE JOINT DEFLECTION OF  A PERFECT FRAME

1.                                                                                  The Unit Load method

2.                                                                                  Deflection   by   Castigliano?s   First   Theore

3.                                                                                  Graphical method : Willot -Mohr Diagram

STATE THE DEFLECTION OF THE JOINT DUE TO LINEAR DEFORMATION

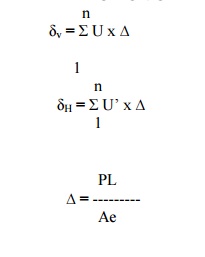
 U= vertical deflection

U?=  horizontal   deflection

THE DEFLECTION OF JOINT DUE TO TEMPERATURE VARIATION n

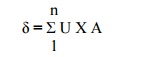
 = U₁?₁ + U₂ ?₂ +   …………+_n?_n U

 If the change in length (?) of certainembers memb  will be substituted as zero in the above equation.

STATE THE DEFLECTION OF A JOINT DUE TO LACK OF FIT n

 = U₁?₁ + U₂ ?₂ +   …………+_n?_n U

 If there is only one member having lack ₁of,the deflectionfit of?a particular joint will be  equal to U₁?_1.

 Determine the vertical and horizontal displacements of the point C of the pin-jointed frame  shown in fig. The cross sectional area of AB is 100 sqmm and of AC and BC 150 mm² each.  E= 2 x 10 ⁵ N/mm². (By unit load method)

Sol:

 The vertical and horizontal deflections of the joint C are given by

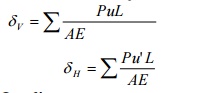
 A) Stresses due to External Loading:

 B) Stresses due to unit vertical load at C:

 Apply unit vertical load at C. The Stresses in each member will be 1/6 than of those  obtained due to external load.

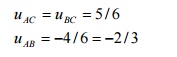
 C) Stresses due to unit horizontal load at C:

 Assume the horizontal load towards left as shown in fig.

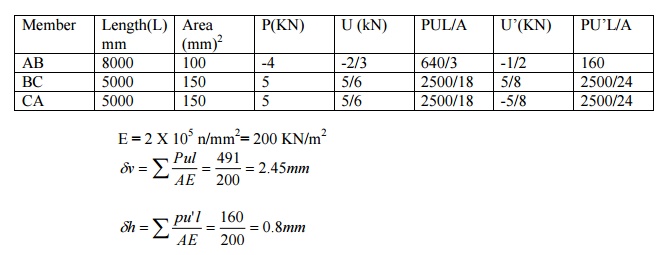
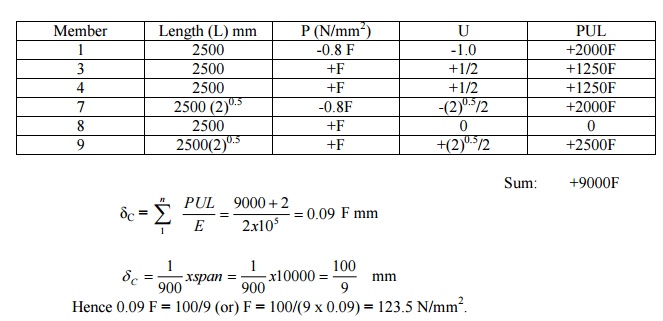
 The frame shown in fig. Consists of four panels each 25m wide, and the cross sectional  areas of the member are such that, when the frame carries equal loads at the panel points  of the lower chord, the stress in all the tension members is f n/mm² and the stress in all the  comparison members of 0.8 f N/mm².Determine the values of f if the ratio of the maximum  deflection to span is 1/900 Take E= 2.0 x 10⁵ N/mm².

 Determine the vertical deflection of the joint C of the frame shown in fig. due to  temperature rise of 60º F in the upper chords only. The coefficient of expansion = 6.0 x 10^-6  per 1º F and E = 2 x 10 ⁶ kg /cm².

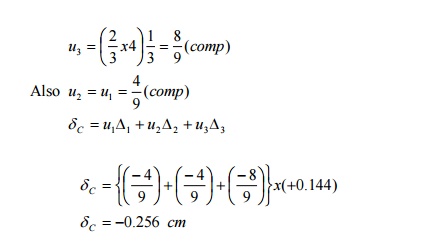
 Using the principle of least work, analyze the portal frame shown in Fig. Also plot the

B.M.D.

Sol:

 The support is hinged. Since there are two equations at each supports. They are H_A, V_A, H_D,  and VD. The available equilibrium equation is three. (i.e.) åM =0, åH =0, åV =0 .

 \ The structure is statically indeterminate to first degree. Let us treat the horizontal H ( ¬) at A  as redundant. The horizontal reaction at D will evidently be = (3-H) ( ¬). By taking moments at  D, we get

 (V_A x 3) + H (3-2) + (3 x 1) (2 -1.5) -(6 x 2) = 0

 V_A = 3.5 -H/3

 V_D = 6 -V_A = 2.5 + H/3

 By the theorem of minimum strain energy,

 (1)For member AB:

 Taking A as the origin.

 (2) For the member BE:

 Taking B as the origin.

 (3) For the member CE:

 Taking C as the origin

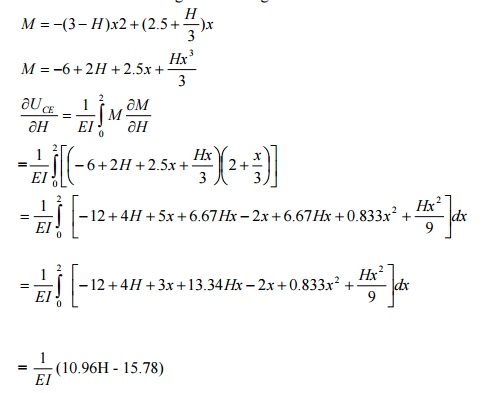
 (4) For the member DC:

 Taking D as the origin

 A simply supported beam of span 6m is subjected to a concentrated load of 45 KN at 2m  from the left support. Calculate the deflection under the load point. Take E = 200 x 10⁶  KN/m² and I = 14 x 10^-6 m⁴.

 R_B = Total load -R_A = 1/3 KN

 Virtual Moment:

 Consider section between AC

 M₁ = 2/3 X₁   [limit 0 to 2]

 Section between CB

 M₂ = 2/3 X₂-1 (X₂-2 ) [limit 2 to 6 ]

 Real Moment:

 The internal moment due to given loading

 M₁= 30 x X₁

 M₂ = 30 x X₂ -45 (X₂ -2)

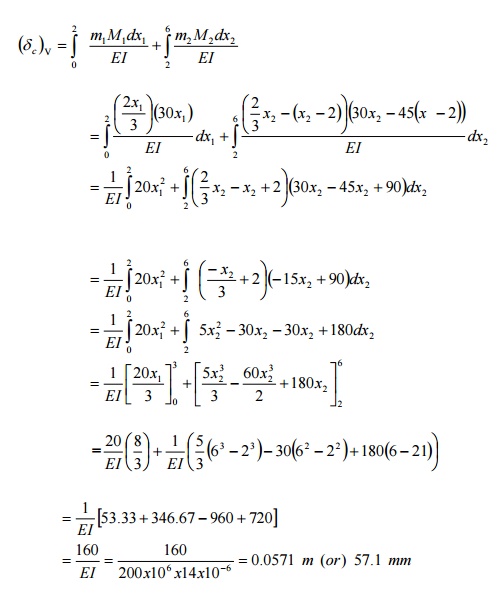
The deflection under the load = 57.1 mm

Define and prove the Maxwell's reciprocal theorem

 The Maxwell?s reciprocal 'The work theorem done stated by the asf due to displacements caused by a second system of loads equals the work done by the second system of loads due to displacements caused by the first system o loads".

Maxwell?s theorem of reciprocal deflection  has the following three versions:

1. The deflection at A due to unit force at B is equal to deflection at B due to unit force at A.

 ?_AB = ?_BA

 2. The slope at A due to unit couple at B is equal to the slope at B due to unit couple A

 ?_AB = ?_BA

 3. The slope at A due to unit load at B is equal to deflection at B due to unit couple.

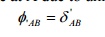
Proof:

 By unit load method,

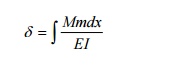
Where,

 M= bending moment at any point x due to external load.

 m= bending moment at any point x due to unit load applied at the point where  deflection is required.

Let m_XA=bending moment at any point x due to unit load at A

Let m_{XB =} bending moment at any point x due to unit load at B.

When unit load (external load) is applied at A,

 M=m_XA

 To find deflection at B due to unit load at A, apply unit load at B.Then m= m_XB

Hence,

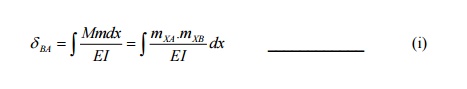
Similarly,

 When unit load (external load) is applied at B, M=m_XB

 To find the deflection at A due to unit load at B, apply unit load at A.then m= m_XA

 Comparing (i) & (ii) we get

 ?AB = BA?

 Using Castigliano's theorem, determine the de  shown in the fig. Take EI = 4.9 MN/m².

Solution:

 Apply dummy load W at B. Since we have to determine the deflection of the free end.  Consider a section xx at a distance x from B. Then

 M _x  =Wx +30(x-1)+20 *1* (x-1.5)+16(x-2)

 A cantilever, 8m long, carrying a point loads 5 KN at the center and an udl of 2 KN/m for a  length 4m from the end B. If EI is the flexural rigidity of the cantilever find the reaction at  the prop.

' A simply supported beam of span L is carrying a concentrated load W at the centre and a uniformly  distributed load of intensity of w per unit leng  the centre of the beam.

Solution:

 Let the load W is applied first and then the uniformly distributed load w.

 Deflection due to load W at the centre of the beam is given by

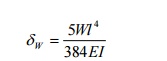
Hence work done by W due to w is given by:

 STATE THE DIFFERENCE BETWEEN UNIT LOAD AND STRAIN ENERGY  METHOD IN THE DETERMINATION OF STRUCTURES.

 In strain energy method, an imaginary load P is applied at the point where the deflection is  desired to be determined. P is equated to zero in the final step and the deflection is obtained.

 In the Unit Load method, a unit load (instead of P) is applied at the point where the deflection  is desired.

 STATE THE ASSUMPTIONS MADE IN THE UNIT LOAD METHOD

2.                  The external and internal forces are in equilibrium

3.                  Supports are rigid and no movement is possible

4.                                                                              The material is strained well within the elastic limit.

5.                                                                              

LOAD METHOD

The deflection by the unit load method is given by n PUL

STATE  MAXWELL'S RECIPROCAL THEOREM

 The Maxwell?s Reciprocal theorem states as  due to displacements caused by a second system of loads equals the work done by the second system  of loads due to displacements caused by the first system of loads.

DEGREE OF REDUNDANCY

 A frame is said to be statically indeterminate when the no of unknown reactions or stress  components exceed the total number of condition equations of equilibrium.

PERFECT FRAME

 If the number of unknowns is equal to the number of conditions equations available, the frame  is said to be a perfect frame.

 STATE THE TWO TYPES OF STRAIN ENERGIES  

c. strain energy of distortion (shear strain energy)

 d.strain energy of uniform compression (or) tension (volumetric strain energy)

STATE  IN WHICH CASES,   CASTIGLIANO'S   THEOREM   CAN

1.                                                              To determine the displacements of complicated structures.

2.                                                                 To find the deflection of beams due to shearing (or) bending forces (or) bending moments are unknown.

3.                                                                 To find the deflections of curved beams springs etc.