Civil - Strength of Materials - Indeterminate Beams

INDETERMINATE BEAMS

1 STATICALLY INDETERMINATE BEAMS

 If the numbers of reaction components are more than the conditions equations, the structure is  defined as statically indeterminate beams.

 E = R -r

 E = Degree of external redundancy

 R = Total number of reaction components

 r = Total number of condition equations available.

 A continuous beam is a typical example of externally indeterminate structure.

2 STATE THE DEGREE OF INDETERMINACY IN PROPPED CANTILEVER

 For a general loading, the total reaction components (R) are equal to (3+2) =5,

 While the total number of condition equations (r) are equal to 3. The beam is statically  indeterminate, externally to second degree. For vertical loading, the beam is statically  determinate to single degree.

 E = R -r

 5 -3 = 2

3 STATE THE DEGREE OF INDETERMINACY IN A FIXED BEAM

 For a general system of loading, a fixed beam is statically indeterminate to third degree. For vertical  loading, a fixed beam is statically indeterminate to second degree.

 E = R -r

For general system of loading: 

R = 3 + 3 and r = 3

 E = 6-3 = 3 

For vertical loading:

 R = 2+2 and r = 2 

E = 4 -2 = 2

4       STATE THE DEGREE OF INDETERMINACY IN THE GIVEN BEAM

 The beam is statically indeterminate to third degree of general system of loading.

 R = 3+1+1+1 = 6

 E = R-r

6-3 = 3

5 STATE THE DEGREE OF INDETERMINACY IN THE GIVEN BEAM

 The beam is statically determinate. The total numbers of condition equations are equal to 3+2 =  5. Since, there is a link at B. The two additional condition equations are at link.

E  = R-r

=  2+1+2-5

=  5-5

 E = 0

6 STATE THE METHODS AVAILABLE FOR ANALYZING STATICALLY  INDETERMINATE STRUCTURES

i.      Compatibility method

ii.      Equilibrium method

 7 WRITE THE EXPRESSION FIXED END MOMENTS AND DEFLECTION FOR A  FIXED BEAM CARRYING POINT LOAD AT CENTRE

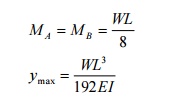
8 WRITE THE EXPRESSION FIXED END MOMENTS AND DEFLECTION FOR A  FIXED BEAM CARRYING ECCENTRIC POINT LOAD

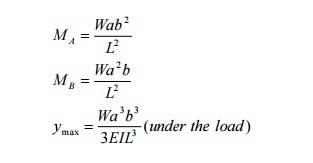
9 WRITE THE EXPRESSION FIXED END MOMENTS FOR A FIXED DUE TO  SINKING OF SUPPORT

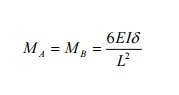
 A fixed beam AB of length 6m carries point load of 160 kN and 120 kN at a distance of 2m and 4m  from the left end A. Find the fixed end moments and the reactions at the supports. Draw B.M and  S.F diagrams.

 A fixed beam AB of length 6m carries two point loads of 30 kN each at a distance of 2m  from the both ends. Determine the fixed end moments and draw the B.M diagram.

 Find the fixing moments and support reactions of a fixed beam AB of length 6m, carrying a uniformly  distributed load of 4kN/m over the left half of the span.

9 STATE THE THEOREM OF THREE MOMENTS 

Theorem of three moments

 It states that 'If BC and CD are only two co  an external loading, then the moments M_B, M _C and M _D at the supports B, C and D are given by

 What are the fixed end moments for a fixed beam of length 'L  load 'w' at a distance 'a' from left end?

 Fixed End Moment:

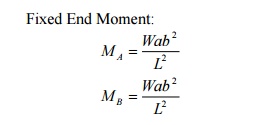
10 EXPLAIN THE EFFECT OF SETTLEMENT OF SUPPORTS IN A CONTINUOUS BEAM

 Due to the settlement of supports in a continuous beam, the bending stresses will alters  appreciably. The maximum bending moment in case of continuous beam is less when compare to the  simply supported beam.

 ADVANTAGES OF CONTINUOUS BEAMS OVER SIMPLY SUPPORTED BEAMS

 (i)The maximum bending moment in case of a continuous beam is much less than in case of a  simply supported beam of same span carrying same loads.

 (ii) In case of a continuous beam, the average B.M is lesser and hence lighter materials of  construction can be used it resist the bending moment.

 A fixed beam of length 5m carries a uniformly distributed load of 9 kN/m run over the  entire span. If I = 4.5x10^-4 m⁴ and E = 1x10⁷ kN/m², find the fixing moments at the ends and deflection at the centre.

 A fixed beam AB, 6m long is carrying a point load of 40 kN at its center. The M.O.I of the  beam is 78 x 10⁶ mm⁴ and value of E for beam material is 2.1x10⁵ N/mm². Determine (i)  Fixed end moments at A and B.

 A fixed beam AB of length 3m is having M.O.I I = 3 x 10⁶ mm⁴ and value of E for beam  material is 2x10⁵ N/mm². The support B sinks down by 3mm. Determine (i) fixed end  moments at A and B.

 A fixed beam AB, 3m long is carrying a point load of 45 kN at a distance of 2m from A. If  the flexural rigidity (i.e) EI of the beam is 1x10⁴kNm². Determine (i) Deflection under the Load.

 A fixed beam of 5m span carries a gradually varying load from zero at end A to 10 kN/m at  end B. Find the fixing moment and reaction at the fixed ends.

 A continuous beam ABC covers two consecutive span AB and BC of lengths 4m and 6m,  carrying uniformly distributed loads of 6kN/m and 10kN/m respectively. If the ends A and  C are simply supported, find the support moments at A,B and C. draw also B.M.D and S.F.D.

 A continuous beam ABCD of length 15m rests on four supports covering 3 equal spans and carries  a uniformly distributed load of 1.5 kN/m length .Calculate the moments and reactions at the  supports. Draw The S.F.D and B.M.D.

 A continuous beam ABCD, simply supported at A,B, C and D is loaded as shown in fig.

 Find the moments over the beam and draw B.M.D and S.F.D.

(i)                B.M.D due to vertical loads taking each span as simply supported:

 (ii) B.M.D due to support moments:

 Since the beam is simply supported M_A =M_D = 0

a)     For spans AB and BC

 Using the theorem of three moments draw the shear force and bending moment diagrams  for the following continuous beam.

 A beam AB of 4m span is simply supported at the ends and is loaded as shown in fig.

 Determine (i) Deflection at C (ii) Maximum deflection (iii) Slope at the end A.

 E= 200 x 10⁶ kN/m² and I = 20 x 10^-6 m⁴

 9. A continuous beam is shown in fig. Draw the BMD indicating salient points.

10. A cantilever beam AB of span 6m is fixed at A and propped at B. The beam carries a udl of  2kN/m over its whole length. Find the reaction at propped end.

Important Questions and Answers

1. Explain with examples the statically indeterminate structures.

If the forces on the members of a structure cannot be determined by using conditions of equilibrium (?Fx =0, ?Fy = 0, ?M = 0 ), it is called statically indeterminate structures.

Example: Fixed beam, continuous beam.

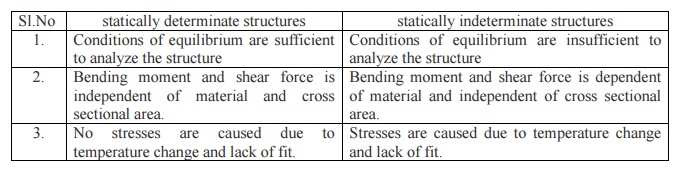
2. Differentiate the statically determinate structures and statically indeterminate structures?

3. Define: Continuous beam.

A Continuous beam is one, which is supported on more than two supports. For usual loading on the beam hogging ( - ive ) moments causing convexity upwards at the supports and sagging ( + ve ) moments causing concavity upwards occur at mid span.

4. What are the advantages of Continuous beam over simply supported beam?

1. The maximum bending moment in case of continuous beam is much less than in case

of simply supported beam of same span carrying same loads.

2. In case of continuous beam, the average bending moment is lesser and hence lighter materials of construction can be used to resist the bending moment.

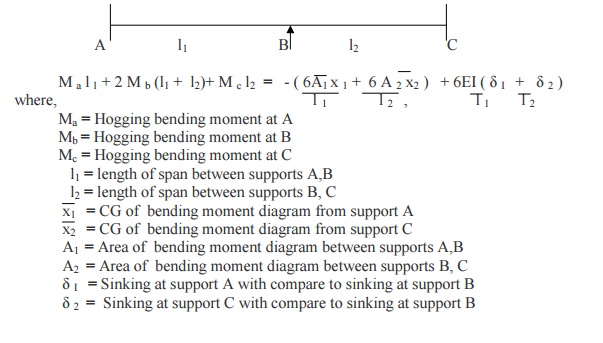
5.Write down the general form of Clapeyron's three moment equations for the continuous beam.

6. Write down the Clapeyron's three moment equations for the continuous beam with sinking at the supports.

7.Write down the Clapeyron's three moment equations for the fixed beam

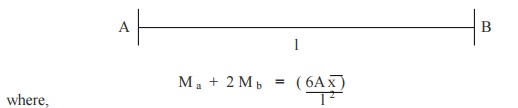
M_a = Hogging bending moment at A M_b = Hogging bending moment at B

l = length of span between supports A,B

x  = CG of  bending moment diagram from support A

A = Area of  bending moment diagram between supports A,B

8. Write down the Clapeyron's three moment equations for the continuous beam carrying UDL on both the spans.

9. Give the values of ( 6A ₁ x ₁ / l ₁ ), ( 6A ₂ x ₂  / l ₂ )   values for different type of loading.

10.     Give the procedure for analyzing the continuous beams with fixed ends using three moment equations?

The three moment equations, for the fixed end of the beam, can be modified by imagining a span of length l ₀ and moment of inertia, beyond the support the and applying the theorem of three moments as usual.

11.                Define Flexural Rigidity of Beams.

The product of young's modulus (E) and moment of inertia (I) is called Flexural

Rigidity (EI) of Beams. The unit is  N mm ².

12. What is a fixed beam?

A beam whose both ends are fixed is known as a fixed beam. Fixed beam is also called as built-in or encaster beam. Incase of fixed beam both its ends are rigidly fixed and the slope and deflection at the fixed ends are zero.

13.                What are the advantages of fixed beams?

(i)                For the same loading, the maximum deflection of a fixed beam is less than that of a simply supported beam.

(ii)             For the same loading, the fixed beam is subjected to lesser maximum bending moment.

(iii)           The slope at both ends of a fixed beam is zero.

(iv)           The beam is more stable and stronger.

14.                What are the disadvantages of a fixed beam?

(i)                Large stresses are set up by temperature changes.

(ii)             Special care has to be taken in aligning supports accurately at the same lavel.

(iii)           Large stresses are set if a little sinking of one support takes place.

(iv)           Frequent fluctuations in loadingrender the degree of fixity at the ends very uncertain.

15.Write the formula for deflection of a fixed beam with point load at centre.

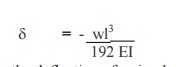
This defection is ¼ times the deflection of a simply supported beam.

15.                        Write the formula for deflection of a fixed beam with uniformly distributed load..

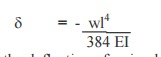
This defection is 5 times the deflection of a simply supported beam.

17. Write the formula for deflection of a fixed beam with eccentric point load..

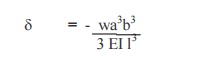
18.                What are the fixed end moments for a fixed beam with the given loading conditions.