Important Questions and Answers: Civil - Strength of Materials - Indeterminate Beams

Important Questions and Answers

1. Explain with examples the statically indeterminate structures.

If the forces on the members of a structure cannot be determined by using conditions of equilibrium (?Fx =0, ?Fy = 0, ?M = 0 ), it is called statically indeterminate structures.

Example: Fixed beam, continuous beam.

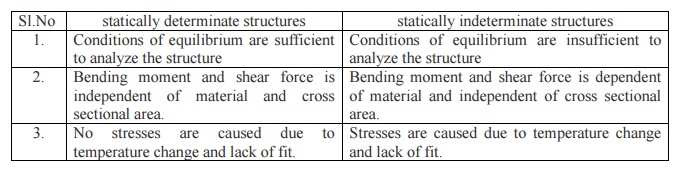
2. Differentiate the statically determinate structures and statically indeterminate structures?

3. Define: Continuous beam.

A Continuous beam is one, which is supported on more than two supports. For usual loading on the beam hogging ( - ive ) moments causing convexity upwards at the supports and sagging ( + ve ) moments causing concavity upwards occur at mid span.

4. What are the advantages of Continuous beam over simply supported beam?

1. The maximum bending moment in case of continuous beam is much less than in case

of simply supported beam of same span carrying same loads.

2. In case of continuous beam, the average bending moment is lesser and hence lighter materials of construction can be used to resist the bending moment.

5.Write down the general form of Clapeyron's three moment equations for the continuous beam.

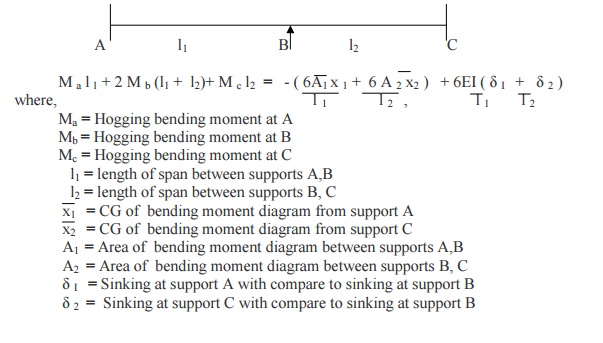
6. Write down the Clapeyron's three moment equations for the continuous beam with sinking at the supports.

7.Write down the Clapeyron's three moment equations for the fixed beam

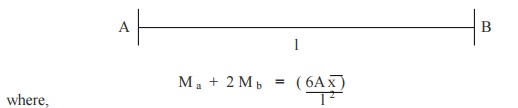
Ma = Hogging bending moment at A Mb = Hogging bending moment at B

l = length of span between supports A,B

x  = CG of  bending moment diagram from support A

A = Area of  bending moment diagram between supports A,B

8. Write down the Clapeyron's three moment equations for the continuous beam carrying UDL on both the spans.

9. Give the values of ( 6A 1 x 1 / l 1 ), ( 6A 2 x 2  / l 2 )   values for different type of loading.

10.     Give the procedure for analyzing the continuous beams with fixed ends using three moment equations?

The three moment equations, for the fixed end of the beam, can be modified by imagining a span of length l 0 and moment of inertia, beyond the support the and applying the theorem of three moments as usual.

11.                Define Flexural Rigidity of Beams.

The product of young's modulus (E) and moment of inertia (I) is called Flexural

Rigidity (EI) of Beams. The unit is  N mm 2.

12. What is a fixed beam?

A beam whose both ends are fixed is known as a fixed beam. Fixed beam is also called as built-in or encaster beam. Incase of fixed beam both its ends are rigidly fixed and the slope and deflection at the fixed ends are zero.

13.                What are the advantages of fixed beams?

(i)                For the same loading, the maximum deflection of a fixed beam is less than that of a simply supported beam.

(ii)             For the same loading, the fixed beam is subjected to lesser maximum bending moment.

(iii)           The slope at both ends of a fixed beam is zero.

(iv)           The beam is more stable and stronger.

14.                What are the disadvantages of a fixed beam?

(i)                Large stresses are set up by temperature changes.

(ii)             Special care has to be taken in aligning supports accurately at the same lavel.

(iii)           Large stresses are set if a little sinking of one support takes place.

(iv)           Frequent fluctuations in loadingrender the degree of fixity at the ends very uncertain.

15.Write the formula for deflection of a fixed beam with point load at centre.

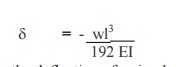
This defection is ¼ times the deflection of a simply supported beam.

15.                        Write the formula for deflection of a fixed beam with uniformly distributed load..

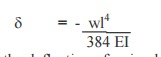
This defection is 5 times the deflection of a simply supported beam.

17. Write the formula for deflection of a fixed beam with eccentric point load..

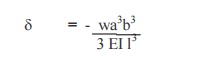
18.                What are the fixed end moments for a fixed beam with the given loading conditions.