Civil - Strength of Materials - Columns

COLUMNS

1 COLUMNS

 If the member of the structure is vertical and both of its ends are fixed rigidly while  subjected to axial compressive load, the member is known as column.

 Example:  A vertical pillar between the roof and floor.

2 STRUTS

 If the member of the structure is not vertical and one (or) both of its ends is Linged (or)  pin jointed, the bar is known as strut.

 Example: Connecting rods, piston rods etc,

3 MENTION THE STRESSES WHICH ARE RESPONSIBLE FOR COLUMN FAILURE.

i.                                                                                                          Direct compressive stresses

ii.                                                                                                        Buckling stresses

iii.                                                                                                     Combined of direct compressive and buckling stresses.

1.                                                                                            The column is initially perfectly straight and the load is applied axially.

2.                                                                                            The cross-section of the column is uniform throughout its length.

3.                                                                                            The  column  material  is  perfectly  elastic,  homogeneous  and  isotropic  and  obeys

 Hooke?s law.

4.                                                                                            The self weight of column is negligible.

4 END CONDITIONS OF COLUMNS

1.                                                                                                        Both the ends of the column are linged (or pinned)

2.                                                                                                        One end is fixed and the other end is free.

3.                                                                                                       Both the ends of the column are fixed.

4.                                                                                                       One end is fixed and the other is pinned.

5 EXPLAIN THE FAILURE OF LONG COLUMN

Solution:

 A long column of uniform cross-sectional area A and of length l, subjected to an axial  compressive load P, as shown in fig. A column is known as long column if the length of the  column in comparison to its lateral dimensions is very large. Such columns do not fail y  crushing alone, but also by bending (also known buckling)

 The load, at which the column just buckles, is known as buckling load and it is less than  the crushing load is less than the crushing load for a long column.

 Buckling load is also known as critical just (or) crippling load. The value of buckling  load for long columns are long columns is low whereas for short columns the value of buckling  load is high.

 The column will fail when maximum stress (i.e) s₀ + s_b  is more the crushing stress f_c.

 In case of long column, the direct compressive stresses are negligible as compared to buckling  stresses. Hence very long columns are subjected to buckling stresses.

6 STATE THE ASSUMPTIONS MADE IN THE EULER'STHEORY.COLUMNAND  EXPLAIN THE SIGN CONVENTIONS CONSIDERED IN COLUMNS.

 The following are the assumptions made   in   the   Euler's   column   t

1.                                                                                                                                The column is initially perfectly straight and the load is applied axially

2.                                                                                                                                The cross-section of the column is uniform throughout its length.

3.                                                                                                                                The column material is perfectly elastic, homogeneous and isotropic and  obeys Hooke?s law.

4.                                                                                                                                The length of the column is very large as compared to its lateral dimensions

5.                                                                                                                                The direct stress is very small as compared to the bending stress

6.                                                                                                                                The column will fail by buckling alone.

7.                                                                                                                                The self-weight of column is negligible.

 The following are the sign conventions considered in columns:

1.                                                                                                        A moment which will tend to bend the column with its convexity towards its  initial centre line is taken as positive.

2.                                                                                                        A moment which will tend to bend the column with its concavity towards its  initial center line is taken as negative.

7 DERIVE THE EXPRESSION FOR CRIP PLING LOAD WHEN THE BOTH ENDS OF  THE COLUMN ARE HINGED

Solution:

 Consider a column AB of length L hinged at both its ends A and B carries an axial

 crippling load at A.

 Consider any section X-X at a distance of x from B.

 Let the deflection at X-X is y.

 \ The bending moment at X-X due to the load P, M = -P.y

8 DERIVE THE EXPRESSION FOR BUCKLING LOAD (OR) CRIPPLING LOAD WHEN  BOTH ENDS OF THE COLUMN ARE FIXED

Solution:

 Consider a column AB of length l fixed at both the ends A and B and caries an axial  crippling load P at A due to which buckling occurs. Under the action of the load P the column will deflect as shown in fig.

Consider any section X-X at a distance x from B.Let the deflection at X-X is y.

 Due to fixity at the ends, let the moment at A or B is M.

 \ Total moment at XX = M -P.y 

Differential equation of the elastic curve is

9 DERIVE THE EXPRESSION FOR CRIPPLING LOAD WHEN COLUMN WITH ONE  END FIXED AND OTHER END HINGED

Solution:

 Consider a column AB of length l fixed at B and hinged at A. It carries an axial crippling  load P at A for which the column just buckles.

 As here the column AB is fixed at B, there will be some fixed end moment at B. Let it be  M. To balance this fixing moment M, a horizontal push H will be exerted at A.

 Consider any section X-X at a distance x from the fixed end B.  Let the deflection at xx is

y.

 Bending moment at xx = H (l-x) - Py

 \Differential equation of the elastic curve is,

10 DERIVE THE EXPRESSION FOR BUCKLING LOAD FOR THE COLUMN WITH  ONE END FIXED AND OTHER END FREE

Solution:

Consider a column AB of length l, fixed at B and free at A, carrying an axial rippling load P at D de to which it just buckles. The deflected form of the column AB is shown in fig. Let the new position of A is A₁.

Let a be the deflection at the free end. Consider any section X-X at a distance x from B.

 Let the deflection at xx is y.

 Bending moment due to critical load P at xx,

 3.11 WRITE THE EXPRESSION FOR CRIPP LING LOAD WHEN THE BOTH ENDSTHEO  COLUMN ARE HINGED

P = Crippling load

E =   Young?s   Modulus

I = Moment of inertia

l = Length of column

12 EXPRESSION FOR BUCKLING LOAD (OR) CRIPPLING LOAD WHEN BOTHDSEN  OF THE COLUMN ARE FIXED

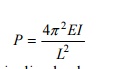
P = Crippling load

E = Young?s   Modulus

I = Moment of inertia 

l = Length of column

13 EXPRESSION FOR CRIPPLING LOAD WHEN COLUMN WITH ONE END FIXED  AND OTHER END LINGED

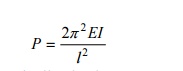
P = Crippling load

E = Young?s   Modulus

I = Moment of inertia 

l = Length of column

14 EXPRESSION FOR BUCKLING LOAD FOR THE COLUMN WITH ONE FIXED AND  OTHER END FREE

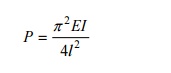
P = Crippling load

E = Young?s   Modulus

I = Moment of inertia 

l = Length of column

15 EXPLAIN EQUIVALENT LENGTH (OR) EFFECTIVE LENGTH

 If l is actual length of a column, then its equivalent length (or) effective length L may be  obtained by multiplying it with some constant factor C, which depends on the end fixation of the  column (ie) L = C x l.

16 WRITE THE EQUIVALENT LENGTH (L) OF THE COLUMN IN WHICH BOTH  ENDS HINGED AND WRITE THE CRIPPLING LOAD

P = Crippling load

E = Young?s   Modulus

I = Moment of inertia 

l = Length of column

17 WRITE THE RELATION BETWEEN EQUIVALENT LENGTH AND ACTUAL  LENGTH FOR ALL END CONDITIONS OF COLUMN.

 A mild steel tube 4m long, 3cm internal diameter and 4mm thick is used as a strut with  both ends hinged. Find the collapsing load, what will be the crippling load if

i.                                                                                                             Both ends are built in?

ii.                                                                                                          One end is built -in and one end is free?

 A column having a T section with a flange 120 mm x 16 mm and web 150 mm x 16 mm is  3m long. Assuming the column to be hinged at both ends, find the crippling load by

6                                                                               2

using                                   Euler's   forKg/cmula..     E   =   2   x   10

 A steel bar of solid circular cross-section is 50 mm in diameter. The bar is pinned at both  ends and subjected to axial compression. If the limit of proportionality of the material is

 210 MPa and E = 200 GPa, determine the m minimum length to which Euler'  formula is valid. Also determine the value  minimum length.

19 CORE (OR) KERNEL OF A SECTION

 When a load acts in such a way on a region around the CG of the section So that in that  region stress everywhere is compressive and no tension is developed anywhere, then that area is called the core (or) Kernal of a section. The kernel of the section is the area within which the line of action of the eccentric load P must cut the cross-section if the stress is not to become tensile.

20 DERIVE THE EXPRESSION FOR CORE OF A RECTANGULAR SECTION

 The limit of eccentricity of a rectangular section b x d on either side of XX axis (or) YY  axis is d/6 to avoid tension at the base core of the rectangular section.

 Core of the rectangular section = Area of the shaded portion

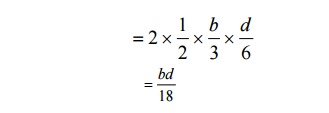
21 DERIVE THE EXPRESSION FOR CORE OF A SOLID CIRCULAR SECTION OF  DIAMETER D

 The limit of eccentricity on either side of both XX (or) YY axis = D/8 to avoid tension of  the base.

 Core of the circular section  = Area of the shaded portion

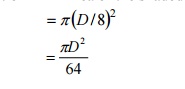
23 A STEEL COLUMN IS OF LENGTH 8M AND DIAMETER 600 MM WITH BOTH  ENDS HINGED. DETERMINE THE CRIPPLING LOAD BY EULER'S

 FORMUL

A. Take E =2.1´10⁵ N/mm².

24 SLENDERNESS  RATIO

It is defined as the ratio of the effective length of the column (L) to the least radius of  gyration of its cross -section (K) (i.e) the ratio of L/K is known as slenderness ratio.

 Slenderness ratio =  L/K

STATE                     THE   LIMITATIONS   OF   EULER'S   FORMULA

25 WRITE THE RANKINE'S   FORMULA   FOR   COLUMNS

 Explain Rankine's and Formula Derive the Rankine's formula column.

Solution:

Rankine's Formula:

 Euler?s formula gives correct results onl  buckling. Whereas Rankine?smulabasedon practicaldevisedexperiments foran empi  determining the crippling or critical load which is applicable to all columns irrespective of

 whether they a short or long.

 If P   is   the   crippling   load   by   Rankine?s   form

 P_c is the crushing load of the column material

 P_E is the crippling load by Euler?s formula.  Then the Empirical formula devised by Rankine

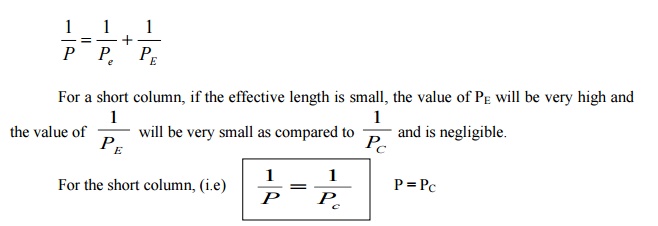
 Thus for the short column, value of crippling load by Rankine is more or less equal to the  value of crushing load:

 A rolled steel joist ISMB 300 is to be used a column of 3 meters length with both ends fixed.  Find the safe axial load on the column. Take factor of safety 3, f_c = 320 N/mm²   and a = 1/7500 .  Properties of the column section.  Area = 5626 mm²,  I _XX = 8.603 x 10⁷ mm⁴  I_yy =4.539 x 10⁷ mm⁴

 A built up column consisting of rolled steel beam ISWB 300 with two plates 200 mm x 10  mm connected at the top and bottom flanges. Calculate the safe load the column  carry, if the length is 3m and both ends are fixed. Take factor of safety 3 f_c = 320 N/mm²   and a ? = 1 / 7500 Take properties of joist: A = 6133 mm² I_XX = 9821.6 x 10⁴ mm⁴ ; I_yy  = 990.1 x 10⁴  mm⁴

 A column of circular section has 150 mm dia and 3m length. Both ends of the column are  fixed. The column carries a load of 100 KN at an eccentricity of 15 mm from the  geometrical axis of the column. Find the maximum compressive stress in the  column section. Find also the maximum permissible eccentricity to avoid tension in  the column section. E = 1 x 10⁵ N/mm²

1.                                                                                            The   assumptions   involved theory.   in   Lame's   T

i.                                                                                                                      The material of the shell is homogenous and isotropic

ii.                                                                                                                    Plane sections normal to the longitudinal axis of the cylinder remain plane  after the application of internal pressure.

iii.                                                                                                                 All the fibres of the material expand (or) contract independently without being  constrained by their adjacent fibres.

2                                                                                             Derivation   of   Lame's   Theory

Consider a thick cylinder

Let 

 r_c=  Inner radius of the cylinder

 r₀=  Outer radius of the cylinder

 P_i=  Internal radial pressure

 P_o=  External radial pressure

L =  Length of the cylinder

 f₂ =  Longitudinal stress.

26 THICK CYLINDER

 If the ratio of thickness of the internal diameter of a cylindrical or spherical shell exceeds  1/20, it is termed as a thick shell.

 The hoop stress developed in a thick shell varies from a maximum value at the inner  circumference to a minimum value at the outer circumference.

 Thickness > 1/20

j.                                                                                                          The material of the shell is Homogeneous and isotropic.

ii.                                                                                                        Plane section normal to the longitudinal axis of the cylinder remains plane after  the application of internal pressure.

iii.                                                                                                     All the fibers of the material expand (or) contact independently without being  constrained by there adjacent fibers.

27 MIDDLE THIRD RULE

 In rectangular sections, the eccentricity „e? must be less than o  greatest eccentricity of the load is b/6 form the axis Y-Y and with respect to axis X -X₁ the  eccentricity does not exceed d/6. Hence the load may be applied with in the middle third of the  base (or) Middle d/3.

 A thick steel cylinder having an internal diameter of 100 mm an external diameter of 200  mm is subjected to an internal pressure of 55 M pa and an external pressure of 7  Mpa. Find the maximum hoop stress.

 A cast iron pipe has 200 mm internal diameter and 50 mm metal thickness. It carries water  under a pressure of 5 N/mm². Find the maximum and minimum intensities of  circumferential stress. Also sketch the distribution of circumferential stress and

 radial stress across the section.

 Explain the stresses in compound thick cylinders.

Solution:

 Consider a compound thick cylinder as shown in fig.

Let,

r₁=  Inner radius of the compound cylinder

 r₂=  Radius at the junction of the two cylinders

 r₃ =  Outer radius of the compound cylinder

 When one cylinder is shrunk over the other, thinner cylinder is under compression and  the outer cylinder is under tension. Due to fluid pressure inside the cylinder, hoop stress will  develop. The resultant hoop stress in the compound stress is that algebraic sum of the hoop  stress due to initial shrinkage and that due to fluid pressure.

a. Stresses due to initial shrinkage:

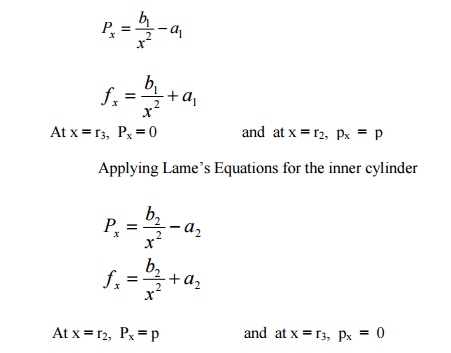
b.  Stresses due to Internal fluid pressure.

 To find the stress in the compound cylinder due to internal fluid pressure alone, the inner and Equation,

A compound cylinder is composed of a tube of 250 mm internal diameter at 25 mm wall  thickness. It is shrunk on to a tube of 200 mm internal diameter. The radial  pressure at the junction is 8 N/mm².

 Find the variation of hoop stress across the  wall of the compound cylinder, if it is under an internal fluid pressure of 60 N/mm²