Chapter: Civil : Strength of Materials : Columns
Solved Problems: Civil - Strength of Materials - Columns
A mild steel tube 4m long, 3cm internal diameter and 4mm thick is used as a strut with both ends hinged. Find the collapsing load, what will be the crippling load if
i. Both ends are built in?
ii. One end is built -in and one end is free?



A column having a T section with a flange 120 mm x 16 mm and web 150 mm x 16 mm is 3m long. Assuming the column to be hinged at both ends, find the crippling load by
6 2
using Euler's forKg/cmula.. E = 2 x 10


A steel bar of solid circular cross-section is 50 mm in diameter. The bar is pinned at both ends and subjected to axial compression. If the limit of proportionality of the material is
210 MPa and E = 200 GPa, determine the m minimum length to which Euler' formula is valid. Also determine the value minimum length.


A rolled steel joist ISMB 300 is to be used a column of 3 meters length with both ends fixed. Find the safe axial load on the column. Take factor of safety 3, fc = 320 N/mm2 and a = 1/7500 . Properties of the column section. Area = 5626 mm2, I XX = 8.603 x 107 mm4 Iyy =4.539 x 107 mm4
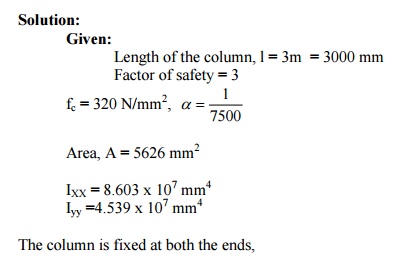

A built up column consisting of rolled steel beam ISWB 300 with two plates 200 mm x 10 mm connected at the top and bottom flanges. Calculate the safe load the column carry, if the length is 3m and both ends are fixed. Take factor of safety 3 fc = 320 N/mm2 and a ? = 1 / 7500 Take properties of joist: A = 6133 mm2 IXX = 9821.6 x 104 mm4 ; Iyy = 990.1 x 104 mm4





A column of circular section has 150 mm dia and 3m length. Both ends of the column are fixed. The column carries a load of 100 KN at an eccentricity of 15 mm from the geometrical axis of the column. Find the maximum compressive stress in the column section. Find also the maximum permissible eccentricity to avoid tension in the column section. E = 1 x 105 N/mm2


A cast iron pipe has 200 mm internal diameter and 50 mm metal thickness. It carries water under a pressure of 5 N/mm2. Find the maximum and minimum intensities of circumferential stress. Also sketch the distribution of circumferential stress and
radial stress across the section.


Explain the stresses in compound thick cylinders.
Solution:
Consider a compound thick cylinder as shown in fig.
Let,
r1= Inner radius of the compound cylinder
r2= Radius at the junction of the two cylinders
r3 = Outer radius of the compound cylinder
When one cylinder is shrunk over the other, thinner cylinder is under compression and the outer cylinder is under tension. Due to fluid pressure inside the cylinder, hoop stress will develop. The resultant hoop stress in the compound stress is that algebraic sum of the hoop stress due to initial shrinkage and that due to fluid pressure.
a. Stresses due to initial shrinkage:
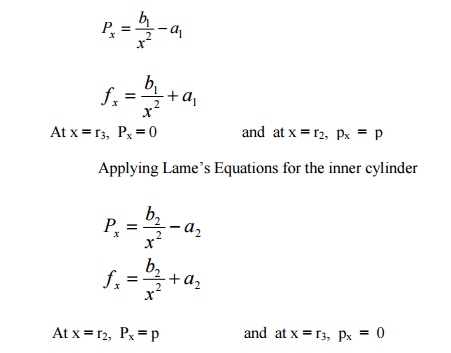
b. Stresses due to Internal fluid pressure.
To find the stress in the compound cylinder due to internal fluid pressure alone, the inner and Equation,

A compound cylinder is composed of a tube of 250 mm internal diameter at 25 mm wall thickness. It is shrunk on to a tube of 200 mm internal diameter. The radial pressure at the junction is 8 N/mm2.
Find the variation of hoop stress across the wall of the compound cylinder, if it is under an internal fluid pressure of 60 N/mm2







