Chapter: Civil : Strength of Materials : Columns
Important Questions and Answers: Civil - Strength of Materials - Columns
Strength
of Materials - Columns
1.Define: Column and strut.
A column is a long vertical slender
bar or vertical member, subjected to an axial compressive load and fixed
rigidly at both ends.
A strut is a slender bar or a member
in any position other than vertical, subjected to a compressive load and fixed
rigidly or hinged or pin jointed at one or both the ends.
2.
What are the types of column
failure?
1.
Crushing failure:
The column will reach a stage, when
it will be subjected to the ultimate crushing stress, beyond this the column
will fail by crushing The load corresponding to the crushing stress is called
crushing load. This type of failure occurs in short column.
2. Buckling failure:
This kind of failure is due to
lateral deflection of the column. The load at which the column just buckles is
called buckling load or crippling load or critical load. This type of failure
occurs in long column.
3. What is slenderness ratio ( buckling factor)? What is its
relevance in column?
It is the ratio of effective length
of column to the least radius of gyration of the cross sectional ends of the
column.
Slenderness ratio = l eff / r
l eff = effective length of column r
= least radius of gyration
Slenderness ratio is used to
differentiate the type of column. Strength of the column depends upon the
slenderness ratio, it is increased the compressive strength of the column
decrease as the tendency to buckle is increased.
4. What are the factors affect the strength column?
1.Slenderness ratio
Strength of the column depends upon
the slenderness ratio, it is increased the compressive strength of the column
decrease as the tendency to buckle is increased.
2.
End conditions: Strength of the column depends upon the end
conditions also.
5.Differentiate
short and long column
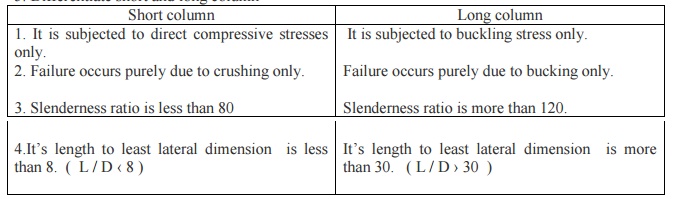
6.What are the
assumptions followed in Euler's equation?
1. The material of
the column is homogeneous, isotropic and elastic.
2. The section of
the column is uniform throughout.
3. The column is
initially straight and load axially.
4. The effect of the
direct axial stress is neglected.
5. The column fails
by buckling only.
7. What are the
limitations of the Euler's formula?
1. It is not valid
for mild steel column. The slenderness ratio of mild steel column is less than 80.
2. It does not take
the direct stress. But in excess of load it can withstand under direct
compression only.
8. Write the
Euler's formula for different end conditions.
1.
Both ends fixed.
2.
Both ends hinged
3.
One end fixed ,other end
4.
One end fixed, other end
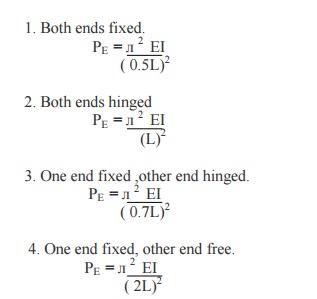
L = Length of the column
9. Define: Equivalent
length of the column.
The distance between adjacent points
of inflection is called equivalent length of the column. A point of inflection
is found at every column end, that is free to rotate and every point where
there is a change of the axis. ie, there is no moment in the inflection points.
(Or)
The equivalent length of the given
column with given end conditions, is the length of an equivalent column of the
same material and cross section with hinged ends , and having the value of the
crippling load equal to that of the given column.
10. What are the uses of south well plot? (column curve).
The relation between the buckling
load and slenderness ratio of various column is known as south well plot.
The south well plot is clearly shows
the decreases in buckling load increases in slenderness ratio.
It gives the exact value of
slenderness ratio of column subjected to a particular amount of buckling load.
11. Give Rakine's formula
and its advantages.
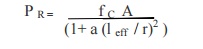
where,
P R = Rakine's critical load
f C =
yield stress
A = cross sectional area
a = Rakine's constant
= effective length
r = radius of gyration
In case of short column or strut,
Eul er's load will be very large. Therefore, Euler's formula is not valid for
short column. To avoid this limitation, Rankine's formula is designed. The
Rankine's formula is applicable for both long and short column.
12. Write Euler's formula for maximum stress for a initially bent column?
? max = P /A + ( M max / Z )

Where, P = axial load
A = cross section area PE
= Euler's load
a = constant
Z = section modulus
13.
Write Euler's formula for
maximum stress for a eccentrically loaded column?

Where, P = axial load
A = cross section area PE
= Euler's load
e = eccentricity
Z = section modulus EI = flexural
rigidity
14. What is beam column? Give examples.
Column having transverse load in
addition to the axial compressive load are termed as beam column.
Eg : Engine shaft, Wing of an
aircraft.
15. Define buckling factor and buckling load.
Buckling factor : It is the ratio between the equivalent length of the column to
the minimum radius of gyration.
Buckling load : The maximum limiting load at which the column tends to have lateral
displacement or tends to buckle is called buckling or crippling load. The
buckling takes place about the axis having minimum radius of gyration, or least
moment of inertia.
16. Define safe load.
It is the load to which a column is
actually subjected to and is well below the buckling load. It is obtained by
dividing the buckling load by a suitable factor of safety (F.O.S).
Safe load =
Buckling load / Factor of safety
17. Write the general expressions
for the maximum bending moment, if the deflection curve equation is given.
BM = - EI ( d 2y / dx 2 )
18. Define thick cylinders.
Thick cylinders are the cylindrical
vessels, containing fluid under pressure and whose wall thickness is not small.
(t ³d/20)
19.
State the assumptions made
in Lame's theory.
i)
The material is homogeneous and
isotropic.
ii)
Plane sections perpendicular to the
longitudinal axis of the cylinder remain plane after the application of
internal pressure.
iii)
The material is stressed within the
elastic limit.
iv)
All the fibres of the material are
to expand or contract independently without being constrained by the adjacent
fibres.
20.
Write Lame's equation to
find out stesses in a thick cylinder.
Radial stress = sr = b - a r2
Circumferential or hoop stress = sc = b + a r2
21. State the variation of hoop stress in a thick cylinder.
The hoop stress is maximum at the
inner circumference and minimum at the outer circumference of a thick cylinder.
22. How can you reduce hoop stress in a thick cylinder.
The hoop stress in
thick cylinders are reduced by shrinking one cylinder over another cylinder.