Chapter: Civil : Strength of Materials : State of Stress in Three Dimensions
Strength of Materials- State of Stress in Three Dimensions
STATE OF STRESS IN THREE DIMENSIONS
1 STRESS
When a certain system of external forces act
on a body then the body offers resistance to
these forces. This internal resistance offered by the body per unit area
is called the stress induced in the
body.
2 PRINCIPAL PLANES
The plane in which the shear stress is zero is
called principal planes. The plane which is
independent of shear stress is known as principal plane.
3 SPHERICAL TENSOR

4 DEVIATOR
STRESS TENSOR
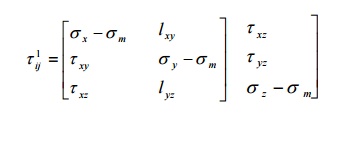
5 THE STRESS COMPONENTS AT A POINT ARE
GIVEN BY THE FOLLOWING ARRAY
Calculate the principal stress and principal
planes.

Solution:
The principal
stresses are the roots of the cubic equation



6 OBTAIN THE PRINCIPAL STRESSES AND THE
RELATED DIRECTION COSINES FOR THE
FOLLOWING STATE OF STRESS




THE STATE OF STRESS AT A POINT IS GIVEN BY
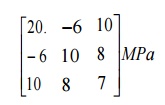
Determine the principal stresses and principal
direction.
Solution:



9 EXPLAIN THE ENERGY OF
DISTORTION ( SHEAR STRAIN ENERGY ) AND DILATATION
The strain
energy can be split up on the following two strain energies.
i.
Strain energy of distortion (shear strain
energy)
ii.
Strain energy of Dilatation (Strain energy of
uniform compression (or)) tension (or)
volumetric strain energy )
Let e1
e2 an d e3 be the
principal strain in the directions of principal stresses s1, s2 and s3.
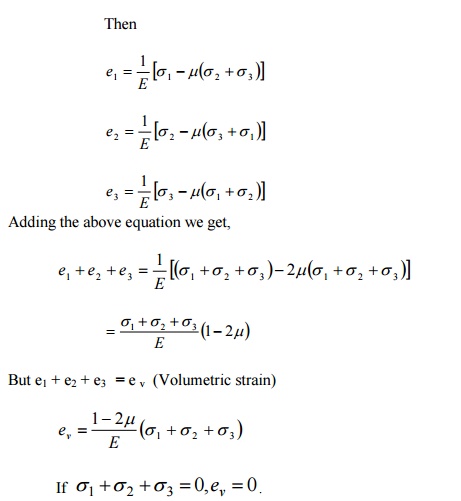
. This means that if sum of the three principal
stress is zero there is no volumetric
change, but only the distortion occurs.
From the
above discussion,
1.
When the sum of three principal stresses
is zero, there is no volumetric change but only the distortion occurs.
2.
When the three principal stresses are equal to
one another there is no distortion but
only volumetric change occurs.
Note:
In the above six theories,
set , sec = Tensile
stress at the elastic limit in simple tension and compression;
s1, s2, s3 = Principal stresses in any complex system
(such that e1 > e2 > e3 )
It may be assumed that the loading is gradual
(or) static (and there is no cyclic (or)
impact load.)
10 STATE THE PRINCIPAL THEORIES OF
FAILURE
1.
Maximum principal stress theory
2.
Maximum shear stress (or) stress difference
theory
3.
Strain energy theory
4.
Shear strain energy theory
5.
Maximum principal strain theory
6.
Mohr?s
Theory
11 LIMITATIONS OF
MAXIMUM PRINCIPAL STRESS THEORY
1.
On
a mild steel
specimen when spiel
tension test is
carried out sliding
occurs approximately 45o
to the axis of the specimen; this shows that the failure in this case is due to maximum shear stress rather than the
direct tensile stress.
2.
It has been found that a material which is
even though weak in simple compression yet
can sustain hydrostatic pressure for in excess of the elastic limit in
simple compression.
12 MAXIMUM PRINCIPAL
STRESS THEORY
According to this theory failure will occur
when the maximum principle tensile stress
(s1)
in the complex system reaches the value of the maximum stress at the elastic
limit (set)
in the simple tension.
13
MAXIMUM SHEAR STRESS THEORY
This theory implies that failure will
occur when the maximum shear stress in
the complex system reaches the value of the maximum shear stress in simple
tension at elastic limit (i.e)

14 LIMITATIONS OF MAXIMUM SHEAR
STRESS THEORY
i.
The theory does not give accurate results for
the state of stress of pure shear in which
the maximum amount of shear is developed (i.e) Torsion test.
ii.
The theory does not give us close results as
found by experiments on ductile
materials. However, it gives safe results.
15 SHEAR STRAIN ENERGY
THEORY
According to this theory the elastic failure
occurs where the shear strain energy per unit
volume in the stressed material reaches a value equal to the shear
strain energy per unit volume at the
elastic limit point in the simple tension test.
16
LIMITATIONS OF DISTORTION ENERGY THEORY
1. The theory does to
agree the experiment results for the material for which sat is quite different etc.
2.
This theory is regarded as one to which
conform most of the ductile material under
the action of various types of loading.
17 MAXIMUM PRINCIPAL STRAIN THEORY
The theory states that the failure of a
material occurs when the principal tensile strain in the material reaches the strain at the
elastic limit in simple tension (or) when the min minimum principal strain (ie ) maximum principal
compressive strain reaches the elastic limit in simple compression.
18 LIMITATIONS IN
MAXIMUM PRINCIPAL STRAIN THEORY
i.
The theory overestimates the behaviour of
ductile materials.
ii.
The theory does no fit well with the
experimental results except for brittle materials
for biaxial tension.
19 STRESS TENSOR IN CARTESIAN COMPONENTS

20 THREE STRESS INVARIANTS
The principal
stresses are the roots of the cubic equation,
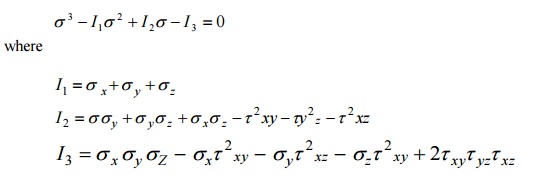
21 TWO TYPES OF STRAIN ENERGY
i.
Strain energy of distortion (shear strain
energy)
ii.
Strain energy of dilatation.
MOHR'S THEORY
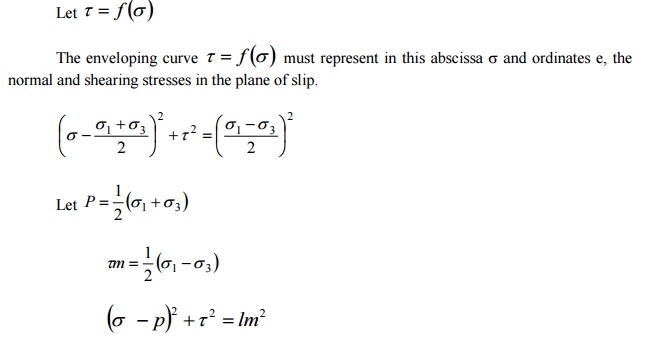
Total Strain Energy Theory
The total strain energy of deformation is
given by

22 EXPLAIN THE MAXIMUM
PRINCIPAL STRESS THEORY:
-
This is the simplest and the oldest theory of
failure
-
According to this theory failure will occur
when the maximum principle tensile
stress (?1)
in the complex system reaches the value of the maximum stress at the elastic limit (?et)
in the simple tension (or) the minimum principal stress (that is, the maximum principal compressive stress),
reaches the elastic limit stress (?)
in simple compression.
(ie.) ?1 = ?et (in simple tension)

-
If the maximum principal stress is the design
criterion, the maximum principal stress
must not exceed the working sfor
the material. Hence,
?1 < ?
-
This theory disregards the effect of other
principal stresses and of the shearing stresses
on other plane through the element. For brittle materials which do not
fail by yielding but fail by brittle
fracture, the maximum principal stress theory is considered to be reasonably satisfactory.
This theory
appears to be approximately correct for ordinary cast -irons and brittle metals.
23 THE MAXIMUM PRINCIPAL STRESS THEORY IS
CONTRADICTED IN THE FOLLOWING CASES:
On a mild steel specimen when simple
tension test is carried out sliding occurs approximately 45o to the
axis of the specimen; this shows that the failure in the case is due to maximum
shear stress rather than the direct tensile stress.
2.
It has been found that a material which is
even though weak in simple compression
yet can sustain hydrostatic pressure for in excess of the elastic limit in simple compression.
24 EXPLAIN THE MAXIMUM
SHEAR STRESS (OR) STRESS DIFFERENCE THEORY
-
This theory implies that failure will occur when the maximum shear stress maximum in the complex system reaches the
value of the maximum shear stress in
simple tension at the elastic limit i.e.
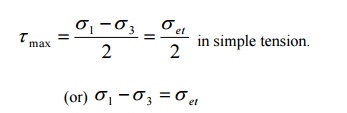
In actual
design set in the above equation is replaced by the safe
stress.
-
This theory gives good correlation with results
of experiments on ductile materials. In
the case of two dimensional tensile stress and then the maximum stress difference
calculated to equate it to set.
Limitations of this theory:
i.
The theory does not give accurate results for
the state of stress of pure shear in
which the maximum amount of shear is developed (ie) Torsion test.
ii.
The theory is not applicable in the case where
the state of stress consists of triaxial
tensile stresses of nearly equal magnitude reducing, the shearing stress
to a small magnitude, so that failure
would be by brittle facture rather than by yielding.
iii.
The theory does not give as close results as
found by experiments on ductile
materials. However, it gives safe results.
25 EXPLAIN THE SHEAR
STRAIN ENERGY THEORY
This theory is also called 'Distortion-Henky E
Theory'
-
According to this theory the elastic failure occurs where the shear strain
energy per unit volume in the stressed
material reaches a value equal to the shear strain energy per unit volume at the elastic limit
point in the simple tension test.
Shear strain energy due to the principal
stresses s1,
s2,
and s3
per unit volume of the stress material.

But for the simple tension test at the elastic
limit point where there is only one principal
stress (ie) set
we have the shear strain energy per unit volume which is given by

The above theory has been found to give best
results for ductile material for which set
=sec
approximately.
Limitations of Distortion energy theory:
1.
Te theory does to agree with the experimental
results for the material for which ?et
is quite different from ?ec.
2. The theory gives ?et =0 for hydrostatic pressure (or) tension, which means that the material will never fail under any hydrostatic pressure (or) tension. When three equal tensions are applied in three principal directions, brittle facture occurs and as such maximum principal stress will give reliable results in this case.
3.
This theory is regarded as one to which
conform most of the ductile material under
the action of various types of loading.
26 EXPLAIN THE MAXIMUM
PRINCIPAL STRAIN THEORY
-
This theory associated with St Venent
-
The theory states that the failure of a
material occurs when the principal tensile
strain in the material reaches the strain at the elastic limit in simple
tension (or) when the minimum principal
strain (ie) maximum principal compressive strain reaches the elastic limit in simple
compression.
Principal strain in the direction of
principal stress ?1,

Limitations:
i.
The theory overestimates the behavior of
ductile materials.
ii.
Te theory does not fit well with the
experimental results except for brittle materials for biaxial tension.
27
EXPLAIN THE STRAIN ENERGY THEORY
The total
stain energy of deformation is given by
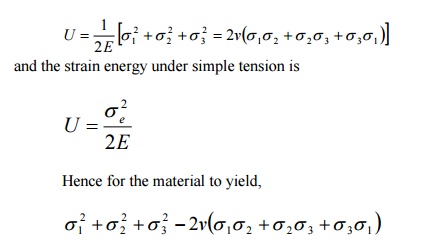
The total elastic energy stored in a material
before it reaches the plastic state can have no
significance as a limiting condition, since under high hydrostatic
pressure, large amount of strain energy
ma be stored without causing either fracture (or) permanent deformation.
28 EXPLAIN
MOHR'S THEORY
A material
may fail either through plastic slip (or) by fracture when either the
shearing stress t in the planes of slip has increased.
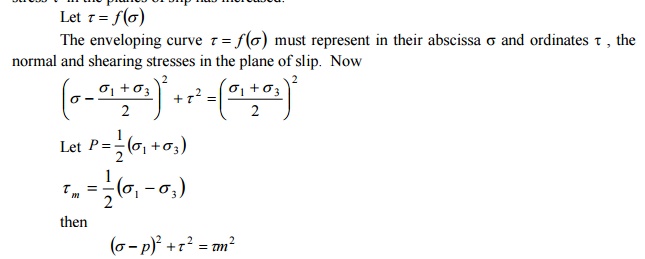
This equation represents the family of
major principal stress circles in parameter form. The equation of this envelope
is obtained by partially differentiating with respect to P
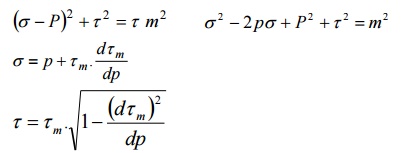
This is to equation of Mohr? principal
stress in parameter form.
IN A STEEL MEMBER, AT A POINT THE MAJOR
PRINCIPAL STRESS IS 180 MN/M2
AND THE MINOR PRINCIPAL STRESSES IS COMPRESSIVE. IF THE TENSILE YIELD POINT OF THE STEEL IS 225 MN/M2,
FIND THE VALUE OF THE MINOR PRINCIPAL
STRESS AT WHICH YIELDING WILL COMMENCE,
ACCORDING TO EACH OF THE FOLLOWING CRITERIA OF FAILURE.
i.
Maximum shearing stress
ii.
Maximum total strain energy
iii.
Maximum shear strain energy
Take Poisson's ratio
= 0.26


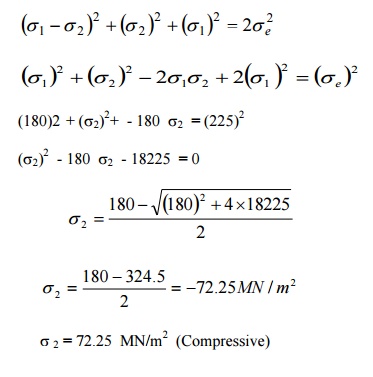
IN A MATERIAL THE PRINCIPAL STRESSES ARE 60
MN/M2, 48 MN/M2 AND - 36
MN/M2. CALCULATE
i.
TOTAL STRAIN ENERGY
ii.
VOLUMETRIC STRAIN ENERGY
iii.
SHEAR STRAIN ENERGY
iv.
FACTOR OF SAFETY ON THE TOTAL STRAIN
ENERGY CRITERIA IF THE MATERIAL YIELDS
AT 120 MN/M2.
TAKE E = 200 GN/M2+ AND 1/M = 0.3



IN A MATERIAL THE PRINCIPAL STRESSES ARE 50
N/MM2, 40 N/MM2 AND - 30 N/MM2, CALCULATE:
i.
TOTAL STRAIN ENERGY
ii.
VOLUMETRIC STRAIN ENERGY
iii.
SHEAR STRAIN ENERGY AND
iv.
FACTOR OF SAFETY ON THE TOTAL STRAIN
ENERGY CRITERION IF THE MATERIAL YIELD
AT 100 N/MM2.
iii.
TAKE E = 200 X 103 N/MM2
AND POISSION RATIO = 0 .28



IN A MATERIAL THE PRINCIPAL STRESSES ARE 50
N/MM2, 40 N/MM2 AND - 30
N/MM2, CALCULATE:
v.
TOTAL STRAIN ENERGY
vi.
VOLUMETRIC STRAIN ENERGY
vii.
SHEAR STRAIN ENERGY AND
viii.
FACTOR OF SAFETY ON THE TOTAL STRAIN
ENERGY CRITERION IF THE MATERIAL YIELD
AT 100 N/MM2.
TAKE E = 200 X 103 N/MM2
AND POISSION RATIO = 0 .28



29 SHEAR STRAIN ENERGY
PER UNIT VOLUME
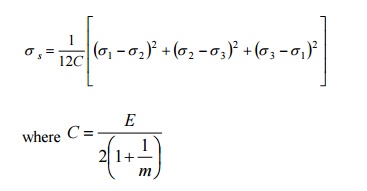
30 THEORIES OF FAILURE
The principal theories are:
1. Maximum principal stress
theory
2. Maximum shear stress (or)
stress difference theory
3. Strain energy theory
4. Shear strain energy theory
5. Maximum principal strain
theory
Related Topics