Image Enhancement: Spatial domain methods

Image Enhancement: Spatial domain methods:

Suppose we have a digital image which can be represented by a two dimensional random field ^A’^y ^ . t r

An image processing operator in the spatial domain may be expressed as a mathematical function L applied to the image f to produce a new image -^v^ “ ^ ^ '^X' -^v^ - as follows.

g{x,y) = T\{x,y)_

The operator ^T applied on ^{f ( x , y)} may be defined over:

A single pixel ^(x,y) . In this case ^T is a grey level transformation (or mapping) function.

Some neighbourhood of ^{( x , y)}.

^T may operate to a set of input images instead of a single image. 

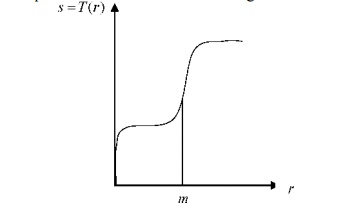
Example 1

The result of the transformation shown in the figure below is to produce an image of higher contrast than the original, by darkening the levels below m and brightening the levels above m in the original image. This technique is known as contrast stretching.

Example 2

The result of the transformation shown in the figure below is to produce a binary image. s = T(r)

Frequency domain methods

Let g( x, y) be a desired image formed by the convolution of an image f (x, y) and a linear, position invariant operator h(x,y), that is:

g(x,y) = h(x,y)2f(x,y)

The following frequency relationship holds:

G(u, i’) = H (a, v)F(u, i’) We can select H (u, v) so that the desired image

g(x,y) = 3^{_ 1} i$(ii,v)F(u,v)

exhibits some highlighted features of f (x,y) . For instance, edges in f (x,y) can be accentuated by using a function H(u,v) that emphasises the high frequency components of F(u,v)