Chapter: Introduction to the Design and Analysis of Algorithms : Transform and Conquer
HornerŌĆÖs Rule and Binary Exponentiation
HornerŌĆÖs Rule and
Binary Exponentiation
In this section, we discuss the problem of
computing the value of a polynomial
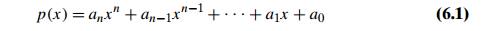
at a given point x and its important special case of computing xn. Polynomials constitute the most important
class of functions because they possess a wealth of good properties on the one
hand and can be used for approximating other types of functions on the other.
The problem of manipulating polynomials efficiently has been important for
several centuries; new discoveries were still being made the last 50 years. By far
the most important of them was the fast Fourier transform (FFT).
The practical importance of this remarkable algorithm, which is based on representing
a polynomial by its values at specially chosen points, was such that some
people consider it one of the most important algorithmic discoveries of all
time. Because of its relative complexity, we do not discuss the FFT algorithm
in this book. An interested reader will find a wealth of literature on the
subject, including reasonably accessible treatments in such textbooks as
[Kle06] and [Cor09].
HornerŌĆÖs Rule
HornerŌĆÖs rule is an old but very elegant and efficient
algorithm for evaluating a polynomial. It is named after the
British mathematician W. G. Horner, who pub-lished it in the early 19th
century. But according to Knuth [KnuII, p. 486], the method was used by Isaac
Newton 150 years before Horner. You will appreciate this method much more if
you first design an algorithm for the polynomial evalu-ation problem by
yourself and investigate its efficiency (see Problems 1 and 2 in this sectionŌĆÖs
exercises).
HornerŌĆÖs rule is a good example of the
representation-change technique since it is based on representing p(x) by a formula different from (6.1). This new formula is obtained
from (6.1) by successively taking x as a common factor in the remaining
polynomials of diminishing degrees:
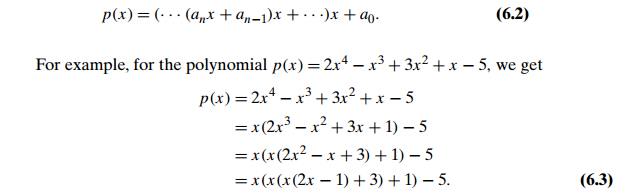
It is in formula (6.2) that we will substitute
a value of x at which the polyno-mial needs to be evaluated. It is hard to
believe that this is a way to an efficient algorithm, but the unpleasant
appearance of formula (6.2) is just that, an appear-ance. As we shall see,
there is no need to go explicitly through the transformation leading to it: all
we need is an original list of the polynomialŌĆÖs coefficients.
The pen-and-pencil calculation can be
conveniently organized with a two-row table. The first row contains the
polynomialŌĆÖs coefficients (including all the coefficients equal to zero, if
any) listed from the highest an to the lowest a0. Except for its first entry, which is an, the second row is filled left to right as
follows: the next entry is computed as the xŌĆÖs value times the last entry in the second row
plus the next coefficient from the first row. The final entry computed in this
fashion is the value being sought.
EXAMPLE 1 Evaluate
p(x) = 2x4 ŌłÆ x3 + 3x2 + x ŌłÆ 5 at x = 3.

Pseudocode of this algorithm is the shortest
one imaginable for a nontrivial algorithm:
ALGORITHM Horner(P [0..n], x)
//Evaluates a polynomial at a given point by
HornerŌĆÖs rule
//Input: An array P [0..n] of coefficients of a polynomial of degree n, // stored from the lowest to the highest and a number x //Output: The value of the polynomial at x
p ŌåÉ P [n]
for i ŌåÉ n ŌłÆ 1 downto
0 do p ŌåÉ x ŌłŚ p + P [i]
return p
The number of multiplications and the number of
additions are given by the same sum:
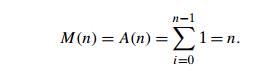
To appreciate how efficient HornerŌĆÖs rule is,
consider only the first term of a polynomial of degree n: anxn. Just computing this single term by the
brute-force algorithm would require n multiplications, whereas HornerŌĆÖs rule
computes, in addition to this term, n ŌłÆ 1 other terms, and it still uses the same
number of multiplications! It is not surprising that HornerŌĆÖs rule is an
optimal algorithm for polynomial evaluation without preprocessing the
polynomialŌĆÖs coefficients. But it took scientists 150 years after HornerŌĆÖs
publication to come to the realization that such a question was worth
investigating.
HornerŌĆÖs rule also has some useful byproducts.
The intermediate numbers generated by the algorithm in the process of
evaluating p(x) at some point x0 turn out to be the coefficients of the quotient of the division of
p(x) by x ŌłÆ x0, and the final result, in addition to being p(x0), is equal to the remainder of this division.
Thus, according to Example 1, the quotient and the remainder of the division of
2x4 ŌłÆ x3 + 3x2 + x ŌłÆ 5 by x ŌłÆ 3 are 2x3 + 5x2 + 18x + 55 and 160, respectively. This division
algorithm, known as synthetic division, is more convenient than so-called long
division.
Binary Exponentiation
The amazing efficiency of HornerŌĆÖs rule fades
if the method is applied to comput-ing an, which is the value of xn at x = a. In fact, it degenerates to the brute-force
multiplication of a by itself, with wasteful additions of zeros in
between. Since computing an (actually, an mod m) is an essential operation in several important
primality-testing and encryption methods, we consider now two algorithms for
computing an that are based on the representation-change
idea. They both exploit the binary representation of exponent n, but one of them processes this binary string left to right,
whereas the second does it right to left.
Let
n = bI
. . . bi . . . b0
be the bit string representing a positive
integer n in the binary number system. This means that the value of n can be computed as the value of the polynomial
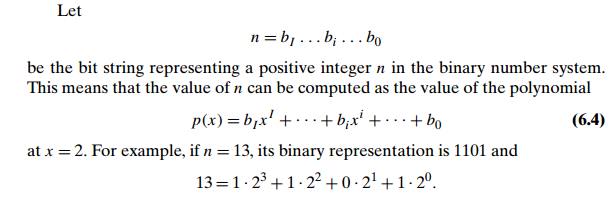
Let us now compute the value of this polynomial
by applying HornerŌĆÖs rule and see what the methodŌĆÖs operations imply for
computing the power

Thus, after initializing the accumulatorŌĆÖs
value to a, we can scan the bit string representing the exponent n to always square the last value of the accumulator and, if the
current binary digit is 1, also to multiply it by a. These observations lead to the following left-to-right
binary exponentiation method of computing an.
ALGORITHM LeftRightBinaryExponentiation(a, b(n))
//Computes an by the left-to-right binary exponentiation
algorithm //Input: A number a and a list b(n) of binary digits bI , . . . , b0
// in the binary expansion of a positive
integer n //Output: The value of an
product ŌåÉ a
for i ŌåÉ I ŌłÆ 1 downto
0 do product ŌåÉ product ŌłŚ product if bi = 1 product ŌåÉ product ŌłŚ a
return product
EXAMPLE 2 Compute a13 by the left-to-right binary exponentiation algorithm. Here, n = 13 = 11012. So we have
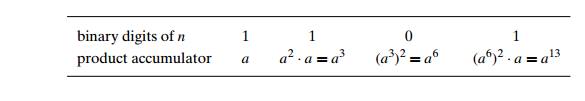
Since the algorithm makes one or two
multiplications on each repetition of its only loop, the total number of
multiplications M(n) made by it in computing an is
(b ŌłÆ 1) Ōēż M(n) Ōēż 2(b ŌłÆ 1),
where b is the length of the bit string representing
the exponent n. Taking into account that b ŌłÆ 1 = log2 n , we can conclude that the efficiency of the
left-to-right binary exponentiation is logarithmic. Thus, this algorithm is in
a better efficiency class than the brute-force exponentiation, which always
requires n ŌłÆ 1 multiplications.
The right-to-left binary exponentiation
uses the same binary polynomial p(2)
(see (6.4)) yielding the value of n. But rather than applying HornerŌĆÖs rule to it as the previous
method did, this one exploits it differently:
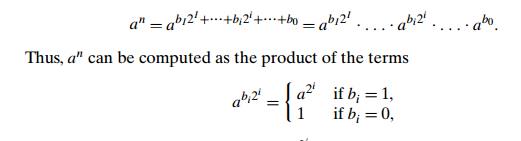
i.e., the product of consecutive terms a2i , skipping those for which the binary digit bi is zero. In addition, we can compute a2i by simply squaring the same term we computed for the previous value of i since a2i = (a2iŌłÆ1)2. So we compute all such powers of a from the smallest to the largest (from right to left), but we
include in the product accumulator only those whose corresponding binary digit
is 1. Here is pseudocode of this algorithm.
ALGORITHM RightLeftBinaryExponentiation(a, b(n))
//Computes an by the right-to-left binary exponentiation
algorithm //Input: A number a and a list b(n) of binary digits bI , . . . , b0
// in the binary expansion of a nonnegative
integer n //Output: The value of an
t erm ŌåÉ a //initializes a2i if b0 = 1 product ŌåÉ a
else product ŌåÉ 1 for i ŌåÉ 1 to I do
t erm ŌåÉ t
erm ŌłŚ t erm
if bi = 1 product ŌåÉ product ŌłŚ t erm return product
EXAMPLE 3 Compute a13 by the right-to-left binary exponentiation method. Here, n = 13 = 11012. So we have the following table filled in from
right to
left:

Obviously, the algorithmŌĆÖs efficiency is also
logarithmic for the same reason the left-to-right binary multiplication is. The
usefulness of both binary exponentia-tion algorithms is reduced somewhat by
their reliance on availability of the explicit binary expansion of exponent n. Problem 9 in this sectionŌĆÖs exercises asks you to design an
algorithm that does not have this shortcoming.
Exercises 6.5
Q. Consider the following brute-force algorithm
for evaluating a polynomial.
ALGORITHM BruteForcePolynomialEvaluation(P [0..n], x)
//Computes the value of polynomial P at a given point x //by the ŌĆ£highest to lowest termŌĆØ brute-force
algorithm
//Input: An array P [0..n] of the coefficients of a polynomial of degree
n, // stored from the lowest to the highest and a number x
//Output: The value of the polynomial at the
point x p ŌåÉ 0.0
for i ŌåÉ n downto 0 do power ŌåÉ 1
for j ŌåÉ 1 to i do
power ŌåÉ
power ŌłŚ x p ŌåÉ p + P [i] ŌłŚ power
return p
Find the total number of multiplications and
the total number of additions made by this algorithm.
Q. Write pseudocode for the brute-force polynomial evaluation that stems from substituting a given value of the variable into the polynomialŌĆÖs formula and evaluating it from the lowest term to the highest one. Determine the number of multiplications and the number of additions made by this algorithm.
Q. a. Estimate how much faster HornerŌĆÖs rule is compared to the ŌĆ£lowest-to-highest termŌĆØ brute-force algorithm of Problem 2 if (i) the time of one multiplication is significantly larger than the time of one addition; (ii) the time of one multiplication is about the same as the time of one addition.
Is
HornerŌĆÖs rule more time efficient at the expense of being less space efficient
than the brute-force algorithm?
a. Apply HornerŌĆÖs rule to evaluate the polynomial
p(x) = 3x4 ŌłÆ x3 + 2x + 5 at
x = ŌłÆ2.
Use the
results of the above application of HornerŌĆÖs rule to find the quo-tient and
remainder of the division of p(x) by x + 2.
Q. Apply HornerŌĆÖs rule to convert 110100101 from binary to decimal.
Q. Compare the number of multiplications and additions/subtractions
needed by the ŌĆ£long divisionŌĆØ of a polynomial p(x) = anxn + anŌłÆ1xnŌłÆ1 + . . . + a0 by
x ŌłÆ c, where c is some constant, with the number of these
operations in the ŌĆ£synthetic division.ŌĆØ
Q. a. Apply the left-to-right binary exponentiation algorithm to compute a17.
Is it
possible to extend the left-to-right binary exponentiation algorithm to work
for every nonnegative integer exponent?
b. Apply the right-to-left binary exponentiation algorithm to compute a17.
Q. Design a nonrecursive algorithm for computing an that mimics the right-to-left binary exponentiation but does not explicitly use the binary representation of n.
Q. Is it a good idea to use a general-purpose polynomial-evaluation algorithm
such as HornerŌĆÖs rule to evaluate the
polynomial p(x) = xn + xnŌłÆ1 + . . . +
x + 1?
Q. According to the corollary of the Fundamental Theorem of Algebra, every polynomial
p(x) = anxn
+ anŌłÆ1xnŌłÆ1 + . . . + a0
can be represented in the form
p(x) = an(x
ŌłÆ x1)(x ŌłÆ x2) . . .
(x ŌłÆ xn)
where x1, x2, . . .
, xn are the
roots of the polynomial (generally, complex and not necessarily distinct).
Discuss which of the two representations is more convenient for each of the
following operations:
polynomial
evaluation at a given point
addition
of two polynomials
multiplication
of two polynomials
Q. Polynomial interpolation Given a set of n data points (xi, yi) where no two xi are the same, find a polynomial p(x) of degree at most n ŌłÆ 1 such that p(xi) = yi for every i = 1, 2, . . . , n.
Related Topics