Growth - Fishes

Growth

Among vertebrates, most growth in mammals and birds is determinate, ceasing after an individual matures. Lower vertebrates exhibit indeterminate growth: growth continues throughout the life span of an individual, although at a constantly decelerating rate. Hence older animals are generally larger, all other things being equal. The caveat here of equality among growth-controlling factors points out another crucial aspect of growth in fishes, namely its plasticity. “Size at age” varies enormously in fishes, whether we are comparing species, populations, individuals within populations, or individuals within cohorts and clutches.

Just about any factor that might possibly influence growth has been shown to have an effect, including temperature, food availability, nutrient availability, light regime, oxygen, salinity, pollutants, current speed, predator density, intraspecific social interactions, and genetics (reviewed by Wootton 1990, 1999). These factors, often working in combination, create large variations in the size of fishes of the same and different ages, leading to so-called size-structured populations, age differences in ecological roles and the ontogenetic niche, and cannibalism.

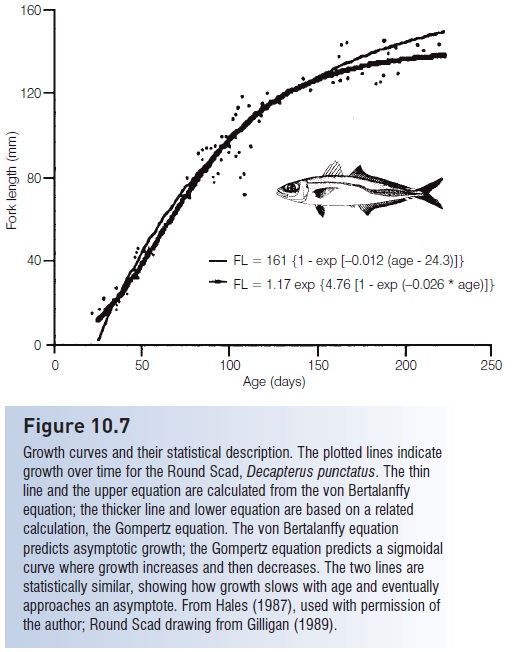
Figure 10.7

Growth curves and their statistical description. The plotted lines indicate growth over time for the Round Scad, Decapterus punctatus. The thin line and the upper equation are calculated from the von Bertalanffy equation; the thicker line and lower equation are based on a related calculation, the Gompertz equation. The von Bertalanffy equation predicts asymptotic growth; the Gompertz equation predicts a sigmoidal curve where growth increases and then decreases. The two lines are statistically similar, showing how growth slows with age and eventually approaches an asymptote. From Hales (1987), used with permission of the author; Round Scad drawing from Gilligan (1989).

When plotted against age, growth curves for fishes appear asymptotic, meaning they tend to flatten out at older ages, although the degree of flatness varies greatly among and within species (Fig. 10.7). This variation forms the basis of an equation commonly used to describe individual growth in most fishes, known as the von Bertalanffy growth equation, which in its simplest form can be written:

Lt = Lmax(1-e-gt)

where L is length, t is a point in time, Lmax is the maximum or asymptotic length attained by the species, e is the base of natural logarithms, and g is the all-important constant that describes the rate at which growth slows. The von Bertalanffy equation is based on bioenergetic considerations, viewing growth as a result of anabolic and catabolic processes by which a fish takes in oxygen and energy to build tissues, and uses up energy and tissue over its life. Many refinements of the equation have been made and alternatives proposed that take into account age- and weight-specific differences in growth, food consumption rates, temperature, and overall energy budgets (see Brett 1979; Gulland 1983; Weatherly & Gill 1987; Busacker et al. 1990; Wootton 1999).

The von Bertalanffy growth coefficient (K) can be useful in assessing fishery management approaches because slower growing fishes with lower K values tend to be more vulnerable to overfishing. Some typical values of K for a variety of fishes are as follows (data courtesy of J. Musick from various sources):

Anchovies, Engraulidae: 0.80–1.40

Tunas, Scombridae: 0.42

Menhaden, Clupeidae: 0.39

Flounder, Paralichthyidae: 0.32–0.40

Spanish mackerels, Scombridae: 0.17–0.35

Epinepheline grouper, Serranidae: 0.18

Porgy, Pagridae: 0.09

Swordfish, Xiphiidae: 0.09–0.19

Ground sharks, Carcharhinidae: 0.04–0.078

The relationship between the increasing mass and length of a fish involves a power function. Mass increases as a function of the cube of the length of the fish, reflecting the universal relationship between the volume and the surface area of a solid, volume increasing faster. Hence the equation for the relationship between mass and length is typically,

M =aLb ,

where M is mass, L is length, and a and b are constants.

The length exponent, b, usually takes values of around 3.0, indicating that the fish is growing isometrically, i.e., that its relative shape is remaining constant as it grows. Values greater or lesser than 3 indicate positive or negative allometric growth (see below), and can serve as an indication of the relative health or condition of the fish.

The equation

K =W L3

can be used to calculate the condition factor, K, of a fish, where W is weight or mass and L is length. Population or cohort measures of K can indicate whether populations or subgroups are growing or feeding at expected rates. Changes in an individual’s condition factor could indicate periods of good versus poor feeding success, disease, or imminent spawning. K is obviously a rough and simplified indicator of general condition and lags far behind any actual events causing changes in relative condition. More precise and accurate indices can be calculated, such as relative condition factor, relative weight, or covariance analysis of mass and length change; much debate exists over which is the best measure (Ricker 1975, 1979; Anderson & Gutreuter 1984; Cone 1990; Wootton 1999).

Because the condition factor tells about an individual’s history rather than its recent experience, measures that minimize the time lag between cause and effect have been developed, including biochemical analysis of protein uptake rate, energy content or intermediary metabolism (RNA : DNA and ADP : ATP ratios), lipid content, and various chemical and biomarker indicators of stress (Busacker et al. 1990; Wedemeyer et al. 1990; Morgan & Iwama 1997; Schreck 2000).