Gravimetric Analysis: Theory

THEORY

The underlying principles and theories of gravimetric analysis are as stated below :

(i)          Law of mass action and reversible reactions,

(ii) Principle of solubility product, and

(iii) Common ion effect.

All the above three aspects shall be described briefly vis-a-vis their direct impact on the gravimetric analysis.

1. LAW OF MASS ACTION AND REVERSIBLE REACTIONS

A plethora of chemical reactions that are intimately associated with the quantitative analysis essen-tially belong to the class of reversible reactions. These reactions under certain prevailing experimental param-eters are made to proceed to completion, whereas in certain other conditions they may even attain equilibrium before completion. In the latter instance, erroneous results may creep in with regard to the pharmaceutical substance under estimation. Hence, it has become absolutely necessary first to establish the appropriate con-ditions whereby the reactions must move forward to attain completion so as to achieve the ultimate objective in all quantitative assays.

In general, there are three cardinal experimental parameters that must be observed rigidly in order to check the reversal processes and help the completion of a reaction, namely :

(a) formation of very slightly ionized molecules,

(b) formation of an insoluble gas, and

(c) formation of a sparingly soluble solid.

The ‘law of mass action’ advocates that the rate of a reaction is directly proportional to the product of the molecular concentrations of the reacting substances. For example :

In the above reaction the rate of reaction of barium chloride with sulphuric acid is designated by the following expression :

Forward reaction :

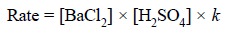            .......................(a)

where, k = a constant that corrects for all factors which affect the rate other than concentration.

Likewise, in the opposing reaction, we have :

Opposing reaction :

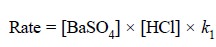            ...........................(b)

where, k₁ = another constant.

At equilibrium the rates of the forward reaction (a) and opposing reaction (b) are equal. Hence, we have :

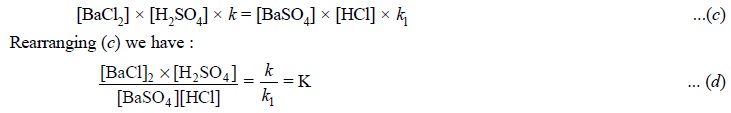
As k and k_l are constants, their quotient K is also a constant known as the equilibrium constant. From Eq. (d), K, the equilibrium constant has a fixed value at a definite temperature, irrespective of concentrations of other components present.

Therefore, if the concentration of sulphuric acid is enhanced, consequently all other concentrations should change accordingly, the concentration of BaCl₂ must become less and that of both BaSO₄ and HCl be proportionately greater so as to maintain the equilibrium constant, thereby having the net impact of shifting the equilibrium towards the right hand side. Evidently, in most quantitative analysis one entity is added invariably to allow the reaction to proceed as closely to completion as possible.

2. PRINCIPLE OF SOLUBILITY PRODUCT

The principle of solubility product may be stated as follows :

‘The product of the concentration of the constituent ions in a saturated solution of a difficultly soluble salt for any given temperature is practically a constant, each concentration being raised to a power equal to the relative number of ions supplied by one molecule of the salt upon dissociating’.

The principle of solubility product is applicable to :

(i) difficultly soluble salts in their saturated solutions,

(ii) occurrence of precipitation,

(iii) prevention of precipitation, and

(iv) dissolution of a substance.

For instance, a difficultly soluble salt ApBq on dissociation provides a relative number of p cations and q anions. Thus, we have :

Hence, solubility product ApBq = [A⁺]^p × [B ^–]^q

where, [ ] are generally used to express the molar concentrations.

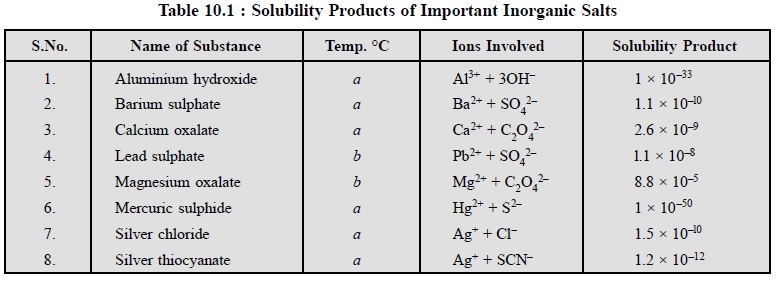
Table 10.1, contains the solubility products of certain difficultly soluble salts generally encountered in pharmaceutical analysis.

The interaction of AgNO₃ and NaCl results into the formation of AgCl which is slightly soluble in water, the solubility being approximately 0.00001 ml litre^–1 i.e., 1.5 mg litre^–1. On exceeding this concentra-tion, the AgCl gets precipitated which remains in equilibrium with the dissolved AgCl. Therefore, at equilib-rium, the clear supernatant liquid is a saturated solution, and at this critical juncture the rate at which the dissolved salt gets precipitated is almost equal to the rate at which the solid undergoes dissolution. This establishes the following equilibria :

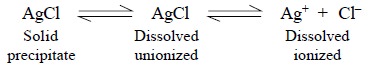
Hence, the ionization equilibrium may be expressed as follows :

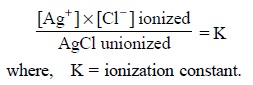
Considering the following two assumptions :

(i) solution remains saturated with AgCl at a aiven temperature, and

(ii) concentration of unionized AgCl remains constant, it follows, that the product K × [AgCl] too becomes constant.

Therefore, it may be inferred that—‘in a saturated solution of a difficultly soluble salt, the product of the molecular concentration of its ions is constant’.

It is an usual practice to express the concentration of the solubility product in terms of moles per litre i.e., molar concentrations.

3. COMNION ION EFFECT

It has been observed that there is no change in the equilibrium constant even if :

(a) the concentrations of reacting components may change, and

(b) the relative concentration of the reacting substances may change.

When a solution of BaCl₂ is added to a solution of sulphuric acid, the sulphate ion for a while is present in a concentration in such a manner that its ionic product with the barium ion exceeds the solubility product of barium sulphate, and the insoluble barium sulphate gets precipitated :

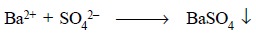
However, at equilibrium the concentration of Ba²⁺ ions shall be exactly equal to the concentration of sulphate ions.

Now, if to the resulting supernatant liquid, which is nothing but a saturated solution of barium sul-phate, an additional small quantity of either a soluble barium salt or a soluble sulphate is provided, a slight further precipitation may occur.

Hence, the equilibrium that represents the ionization constant may be expressed as :

From Eq. (a), it may be derived that if the concentration of Ba²⁺ ion is enhanced by the addition of a soluble barium salt, the concentration of sulphate ion should decrease simultaneously and conversely, that if the concentration of sulphate ion is enhanced by the addition of a soluble sulphate salt, the concentration of Ba²⁺ ion should decrease as their product almost remains constant. Evidently, this decrease in the concentration of the ions in either instance may be achieved by the combination of barium and sulphate ions to give rise to the insoluble barium sulphate thereby forcing the reaction towards completion.

In short, the common-ion effect is employed invariably in carrying out the gravimetric analysis of pharmaceutical substances so as to drive reactions toward completion.

Calculations : In gravimetric analysis the percentage of the desired constituent may be achieved by the following expression :

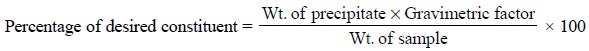
The term ‘gravimetric factor’ is generally employed which represents the number of grams of the desired constituent in 1 g of the substance weighed. It can be further expatiated with the help of the following examples :

(i)          One mole of BaSO₄ (233.39 g) contains one mole of SO₄ atoms (96.06 g).

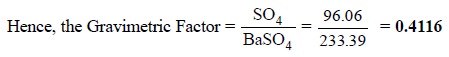
(ii)       One mole of AgCl (143.323 g) contains one mole of Cl atoms (35.453 g).