Geometrical Approach to Multiplication of Monomials

Geometrical Approach to Multiplication of Monomials

We have already learnt that the operation of multiplication can be modelled in different ways. The one that we use in this unit is the representation of multiplication as a product table that is similar to area.

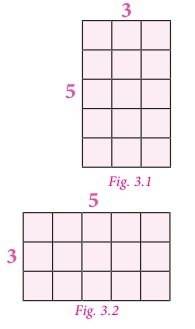
For example, the product 5×3 can be represented as shown in Fig. 3.1, which has five rows and three columns and it comprises 15 small squares. From Fig. 3.2, it is also clear that the product of 5×3 is the same as the product of 3×5 [Since, multiplication is commutative].

Here, multiplication is represented using grid model. The same can be represented using area model.

The area model helps us to understand multiplication by decomposing the area of large rectangle into areas of smaller rectangles. Also the same example which is discussed above may be decomposed as

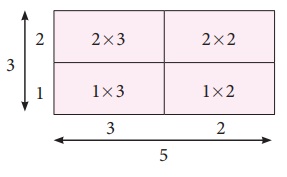
5×3 =(2×3) + (2×2) + (1×3) + (1×2)

        = 6+4+3+2

        =15

This decomposition model is very useful when we are finding the product of large numbers.

Think

Is it the only way to decompose the numbers representing length and breadth? Discuss.

Solution:  No, for example 15 can be decompose into 1 × 15, 3 × 5, 5 × 3, 15 × 1

Note

It can be practiced not to draw the area models in proportions to the numbers, since it stimulates abstract representation.

Let us try to extend this concept of multiplication for variables.

Take few tiles in rectangular shape of length ‘x’ and breadth ‘y’. Also the area of one

tile is xy (  ).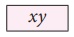

Arrange them as shown in Fig. 3.3 and try to find its area.

In Fig. 3.3, 6 tiles create a rectangular shape. Area of each tile is xy, hence the area of the shape is 6× xy =6xy .          ……(1)

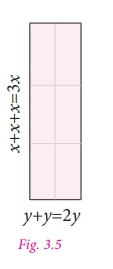
The same area can also be found out by taking the length of the rectangular shape (Fig. 3.4) as x + x + x =3x and breadth as y + y =2 y.

Hence, its area = 3x×2 y     …………(2)

Also, the same area (6xy) can be represented by taking the length of the rectangular shape as y+y=2y and the breadh as x+x+x=3x.

Then the area of the rectangular shape (Fig. 3.5) so obtained = 2y × 3x.  ...(3)

Since all the areas are same, from (1), (2) and (3) we get,

6xy = 3x × 2y = 2y × 3x.

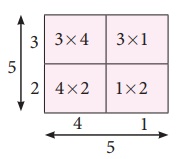
In our earlier discussion, we saw the geometrical representation of 5×3 (Fig. 3.1). Here we shall replace the second number 3 with 5.We get, 5× 5 .

We get the square number 5² = 25 , that may be represented as

5² =(3×4) +(1×3) +(4×2) +(1×2)

=12+3+8+2

=25

Extending the same for variables in Fig. 3.5, the rectangular area is made into a square by making the length equal to breadth, that is 2y is taken as 3x which becomes the side of the square.

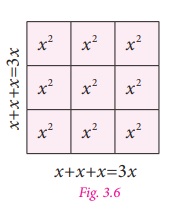
Now in Fig. 3.6 the sides are 3x and area of the square is 3x × 3x        …..(4)

Also, each area is x² and since there are 9 small squares the area of whole square is 9x² . ...(5)

Since both the areas [(4) and (5)] are equal, we get 3x× 3 x =9x² .

Let us find the product of x and (a +b). Look at the following figure.

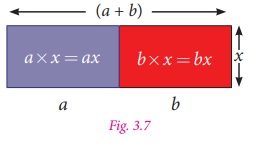
In the Fig. 3.7, the two rectangles are combined together to form a new rectangle. Breadth of each of the rectangle are x and their lengths are a and b. So, the length and breadth of the new rectangle are (a +b) and x respectively.

Thus,

Area of Bigger rectangle = Area of rectangle 1 + Area of rectangle 2

Therefore, (a +b) × x = (a ×x) + (b ×x) [Distributive property]

                                =ax +bx .

Now, we can conclude that the multiplication of two or more monomials, as given below.

Note

Product of monomials is also a monomial.

1. If the variables are same in both the monomials then,

* multiply the numerical co-efficient of the two monomials, separately.

* multiply the same variable by using the product rule of exponents, that is,

 a^m × a ⁿ =a^m+n . For example, x×x = x¹ × x¹ = x¹⁺¹ = x² .

Also, 3x² × 2 x³ =(3× 2)(x² × x³ ) = 6 × x^{2 +3} =6x⁵ .

2. If the variables are different in both the monomials, then multiply them by expressing it as a product of the variables. For example, 5x× 4y =(5× 4) ×(x× y ) =20xy .

Try these

1. Observe the following figures and try to find its area, geometrically. Also verify the same by multiplication of monomial.

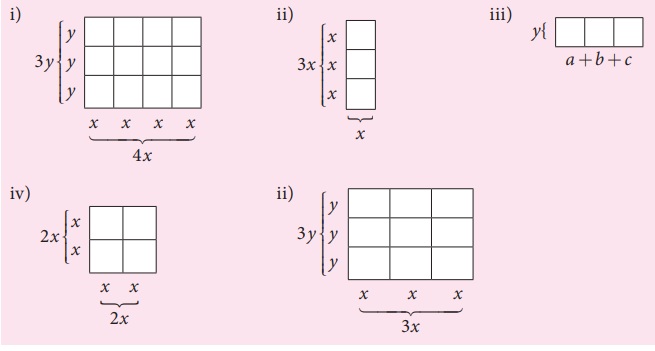
Solution:

(i) Area of each box = xy

Totally 12 boxes

∴ Total area = 12 × xy = 12xy

Also multiplying the length 4x and breadth 3y

We have area of the rectangle = 4x × 3y = 12xy

(ii) Area of each small box = x²

Total number of boxes = 3

∴ Total area = 3x²

Also length of the rectangle = 3x

breadth of the rectangle = x

Area of the rectangle = length × breadth

= 3x × x

 = 3x²

(iii) Area of each small box is ay, by, cy

∴ Total area = ay + by + cy = y (a + b + c)

Area of the rectangle = length × breadth

 = (a + b + c) y

(iv) Area of each small square = x²

There are 4 small squares

∴ Total area of the given square = 4x²

Also side of the big square = 2x

∴ Area of the square = (2x)² = 4x²

(v) Area of each small rectangle = xy

There are 9 such rectangles

∴ Total area = 9xy

Area of big rectangle = length × breadth

= 3x × 3y = 9xy

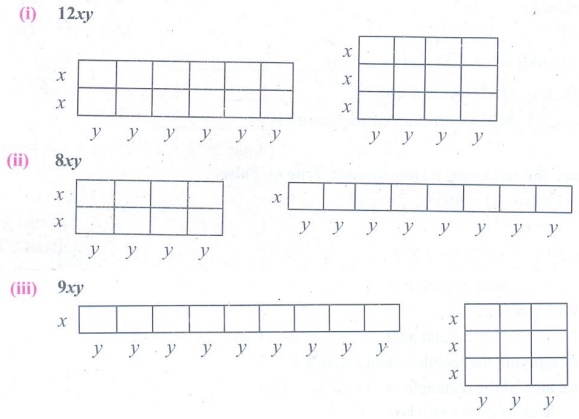
2. Let the length and breadth of a tile be x and y respectively. Using such tiles construct as many rectangles as you can and find out the length and breadth of the rectangles so formed such that its area is

(i) 12xy (ii) 8xy (iii) 9xy

Solution: