Exercise 3.3

Exercise 3.3

Miscellaneous Practice problems

1. Using identity, find the value of

( i) (4.9)²

(ii) (100.1)²

(iii) (1.9)×(2.1)

Solution:  

(i) (4.9)²

(4.9)² = (5 – 0.1)²

Substituting a = 5 and b = 0.1 in

(a – b)² = a² – 2ab + b², we have

(5 – 0.1)² = 5² – 2 (5) (0.1) + (0.1)²

(4.9)² = 25 – 1 + 0.01 = 24 + 0.01

(4.9)² = 24.01

(ii) (100.1)²

(100.1)² = (100 + 0.1)²

Substituting a = 100 and b = 0.1 in

(a + b)² = a² + 2ab + b², we have

(100 + 0.1)² = (100)² + 2 (100) (0.1) + (0.1)²

(100.1)² = 10000 + 20 + 0.01

(100.1)² = 10020.01

(ii) (1.9) × (2.1)

(1.9) × (2.1) = (2 – 0.1) × (2 + 0.1)

Substituting a = 100 and b = 0.1 in

(a – b)(a + b) = a² – b², we have

(2 – 0.1)(2 + 0.1) = 2² – (0.1)²

(1.9) × (2.1) = 4 – 0.01

(9.9) (2.1) = 3.99

2. Factorise : 4x ² − 9 y²

Solution:

4x² – 9y² = 2² x² – 3² y² = (2x)² – (3y)²

Substituting a – 2x and b = 3y in

(a² – b²) = (a + b) (a – b), we have

(2x)² – (3y)² = (2x + 3y) (2x – 3y)

∴ Factors of 4x² – 9y² are (2x + 3y) and (2x – 3y)

3. Simplify using identities (i) (3 p + q )(3 p +r) (ii) (3 p + q )(3p − q)

Solution:

(i) (3p + q)(3p + r)

Substitute x = 3p, a = q and b = r in

(x + a) (x + b) = x² + x(a + b) + ab

(3p + q)(3p + r) = (3p)² + 3p (q + r) + (q × r)

= 3² p² + 3p (q + r) + qr

(3p + q)(3p + r) = 9p² + 3p (q + r) + qr

(ii) (3p + q)(3p – q)

Substitute a  = 3p and b = q in

(a + b) (a – b) = a² – b², we have

(3p + q)(3p – q) = (3p)² – q² = 3²p² – q²

(3p + q)(3p – q) = 9p² – q²

4. Show that (x + 2 y)² −(x − 2y)² =8xy

Solution:

[∵ (a + b)2 = a2 + 2ab + b2

(a – b)2 = a2 – 2ab + b2] 

LHS = (x + 2y)² – (x – 2y)²

= x² + (2 × x × 2y) + (2y)² – [x² – (2 × x × 2y) + (2y)²]

== x² + 4xy + 4y² –[x² – 4xy + 2² y²]

= x² + 4xy + 4y² – x² + 4xy –4 y²

= x² – x² + 4xy + 4xy + 4y² – 4y²

= x² (1 − 1) + xy (4 + 4) + y² (4 − 4)

= 0x² + 8xy + 0y² = 8xy = RHS

∴ (x + 2y)² – (x – 2y)² = 8xy

5. The pathway of a square paddy field has 5 m width and length of its side is 40 m. Find the total area of its pathway. (Note: Use suitable identity)

Solution:

Given side of the square = 40 m

Also width of the pathway = 5 m

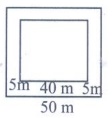
∴ Side of the larger square =. 40m + 2(5)m = 40m + 10m = 50m 

Area of the path way = area of large square – area of smaller square

= 50² – 40²

Substituting a = 50 and b = 40 in

a² – b² = (a + b)(a – b) we have

50² – 40² = (50 + 40) (50–40)

Area of pathway = 90 × 10

Area of the pathway = 900 m²

Challenge Problems

6. If X = a² −1 and Y = 1 −b² , then find X +Y and factorize the same.

Solution:  

Given X = a² – 1

Y = 1 – b²

X + Y = (a²– 1) + (1 – b²)

= a² – 1 + 1 – b²

We know the identity that a² – b² = (a + b) (a – b)

∴ X + Y = (a + b) (a – b)

7. Find the value of (x − y )(x + y)(x² + y² )

Solution:  

We know that (a – b) (a + b) = a² – b² ... (1)

Put a = x and b = y in the identity (1) then

(x – y)(x + y) = x² – y²

Now (x – y) (x + y)(x² + y²) = (x² – y²) (x² + y²)

Again put a = x² and b = y² in (1)

We have (x² – y²) (x² + y²) = (x²)² – (y²)² = x⁴ – y⁴

So (x – y)(x + y) (x² + y²) = x⁴ – y⁴

8. Simplify (5x − 3 y)² −(5x +3y)²

Solution:  

We have the identities …….. (1)

(a + b)² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

So (5x – 3y)² – (5x + 3y)² = (5x)² – (2 × 5x × 3y) + (3y)² – [(5x)² + 2(5x) (3y) + (3y)²]

= 5²x² – 30xy + 3²y² – [5²x² – 30xy + 3²y²]

= 25x² – 30xy + 9y² – [25x² + 30xy + 9y²]

= 25x² – 30xy + 9y² – 25x² – 30xy – 9y²

= x² (25–25) – xy (30 + 30) + y² (9 – 9)

= 0x² – 60xy + 0y² = – 60 xy

∴ (5x – 3y)² – (5x + 3y)² = –60xy

9. Simplify: (i) (a+b)² – (a–b)²  (ii) (a+b)² + (a–b)²

Solution:  

Applying the identities

(a + b)² = a² + 2ab + b²

(a –b)² = a² – 2ab + b²

(i) (a + b)² – (a –b)² = a² + 2ab + b²– [a² – 2ab + b²]

= a² + 2ab + b²– a² + 2ab – b²

= a² (1 – 1 ) + ab (2 + 2 ) + b² ( 1 – 1)

= 0a² + 4ab + 0b² = 4ab

(a + b)² – (a –b)² = 4 ab

(ii) (a + b)² + (a –b)² = a² + 2ab + b² + (a² – 2ab + b² )

= a² + 2ab + b² + a² – 2ab + b²

= a² (1 + 1 ) + ab (2 – 2 ) + b² ( 1 + 1)

= 2a² + 0ab + 2b²  = 2a² + 2b² = 2 (a² + b²)

∴ (a + b)² – (a – b)² = 2(a² + b²)

10. A square lawn has a 2 m wide path surrounding it. If the area of the path is 136 m² , find the area of lawn.

Solution:  

Let the side of the lawn = a m

then side of big square = (a + 2(2))m

 = (a + 4)m

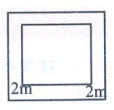
Area of the path = Area of large square – Area of smaller square

136 = (a + 4)² – a²

136 = a² + (2 × a × 4) + 4² – a²

136 = a² + 8a + 16 – a²

136 = 8a + 16

136 = 8 (a + 2)

Dividing by 8

17 = a + 2

Subtracting 2 on both sides

17 – 2 = a + 2 – 2

15 = a

∴ Side of small square = 15m

Area of Square = (Side × Side) Sq. units.

∴ Area of the lawn = (15 × 15)m² = 225 m²

∴ Area of the lawn = 225 m²

11. Solve the following inequalities.

(i) 4n + 7 ≥ 3n + 10, n is an integer.

(ii) 6(x + 6) ≥ 5(x − 3), x is a whole number.

(iii) −13 ≤ 5x + 2 ≤ 32, x is an integer.

Solution:  

(i) 4n + 7 > 3n + 10, n is an integer.

Subtracting 3n both sides

4n + 7 – 3n   ≥  3n + 10 – 3n

n(4 – 3) + 7   ≥  3n + 10 – 3n

n (4 – 3) + 7   ≥  n (3 – 3) + 10

n + 7 ≥ 10

Subtracting 7 on both sides

n + 7 – 7 ≥ 10 – 7

n ≥ 3

Since the solution is an integer and is greater than or equal to 3, the solution will be 3, 4, 5, 6, 7,...

n = 3, 4, 5, 6, 7,...

(ii) 6(x +6) ≥ 5(x – 3), x is a whole number.

6x + 36 ≥ 5x – 15

Subtracting 5x on both sides

6x + 36 – 5x ≥ 5x – 15 – 5x

x(6 – 5) + 36 ≥ x (5 – 5) – 15

x + 36 ≥ – 15

Subtracting 36 on both sides

x + 36 – 36 ≥ –15 –36

 x ≥ –51

The solution is a whole number and which is greater than or equal to –51

∴ The solution is 0, 1, 2, 3, 4,...

x = 0, 1,2, 3, 4,...

(iii) –13 ≤ 5x + 2 ≤ 32, x is an integer.

Subtracting throughout by 2

–13 –2 ≤ 5x + 2 – 2 ≤ 32 – 2

–15 ≤ 5x ≤ 30

Dividing throughout by 5

–15/5   ≤   5x/5   ≤   30/5

– 3 ≤ x ≤ 6

∴ Since the solution is an integer between –3 and 6 both inclusive, we have the solution as –3, –2, –1,0, 1,2, 3, 4, 5, 6.

i.e. x = –3, –2, 0, 1, 2, 3, 4, 5 and 6.

ANSWERS:

Exercise 3.3

1. (i) 24.01 (ii) 10020.01 (iii) 3.99

2. (2x + 3y) (2x – 3y)

3. (i) 9p² + 3p (q + r) + qr (ii) 9p² – q²

4. 900 sq.m

Challenge problems

6. (a – b) (a + b)

7. x⁴ – y⁴

8. –60xy

9. (i) 4ab (ii) 2(a² + b²)

10. 225 sq.m

11. (i) n = 3, 4, 5, 6, ....  (ii) x = 0, 1, 2, 3, ...  (iii) x = –3, –2, –1, 0, 1, 2, 3, 4, 5 and 6