Exercise 3.1

Exercise 3.1

1. Fill in the blanks

(i) ( p − q)² = ----------------------------. [Answer: p²–2pq + q²]

(ii) The product of (x + 5) and (x − 5) is ----------------------. [Answer: x² – 25]

(iii) The factors of x² − 4x + 4 are -----------------------------. [Answer: (x – 2) and (x – 2)]

(iv) Express 24ab²c² as product of its factors is ---------. [Answer: 2 × 2 × 2 × 3 × a × b × b × c × c ]

2. Say whether the following statements are True or False.

(i) (7x + 3)(7x − 4) = 49x² −7x −12 . [Answer: True]

(ii) (a − 1)² =a² −1 . [Answer: False]

(iii) (x ² + y ² )( y ² + x² ) = ( x² + y² )² . [Answer: True]

(iv) 2p is the factor of 8pq. [Answer: True]

3. Express the following as the product of its factors.

(i) 24 ab²c².

(ii) 36 x³y²z.

(iii) 56 mn²p².

Solution:  

(i) 24ab²c² = 2 × 2 × 2 × 3 × a × b × b × c × c

(ii) 36 x³y²z = 2 × 2 × 3 × 3 × x × x × x × y × y × z

(iii) 56 mn²p² = 2 × 2 × 2 × 7 × m × n × n × p × p

4. Using the identity (x +a)(x +b) = x ² + x(a + b) +ab , find the following product.

(i) (x + 3)(x + 7)

(ii) (6a + 9)(6a − 5)

(iii) (4x + 3y)(4x + 5y)

(iv) (8 + pq)(pq + 7)

Solution:  

(i) (x + 3)(x + 7)

Let a = 3;   b = 7, then

(x + 3)(x + 7) is of the form x² + x (a + b) + ab

(x + 3)(x + 7) = x² + x(3 + 7) + (3 × 7) = x²+ 10x + 21

(ii) (6a + 9)(6a – 5)

Substituting x = 6a ;   a = 9 and b = –5

In (x + a) (x + b) = x² + x (a + b) + ab, we get

(6a + 9)(6a – 5) = (6a)² + 6a (9 + (–5)) + (9 × (–5))

= 6² a² + 6a (4) + (–45) = 36a² + 24a – 45

(6a + 9) (6a –5) = 36a² + 24a – 45

(iii) (4x + 3y)(4x + 5y)

Substituting x = 4x ; a = 3y and b = 5y in

(x + a) (x + b) = x² + x (a + b) + ab, we get

(4x + 3y)(4x – 5y) = (4x)² + 4x (3y + 5y) + (3y) (5y)

                                = 4² x² + 4x (8y) + 15y² = 16x² + 32xy + 15y²

(4x + 3y)(4x + 5y) = 16x² + 32xy + 15y²

(iv) (8 + pq ) ( pq + 7)

Substituting x = pq ; a = 8 and b = 7 in

(x + a) (x + b) = x² + x (a + b) + ab, we get

(pq + 8)(pq + 7) = (pq)²+ pq (8 + 7) + (8) (7)

= p² q² + pq (15) + 56

(8 + pq)(pq + 7) = p² +q² + 15pq + 56 

5. Expand the following squares, using suitable identities.

(i) (2x +5)²

(ii) (b -7)²

(iii) (mn +3p)²

(iv) (xyz -1)²

Solution:  

(i) (2x + 5)²

Comparing (2x + 5)² with (a + b)² we have a = 2x and b = 5

a = 2x and b = 5,

(a + b)² = a² + 2ab + b²

(2x + 5)² = (2x)² + 2(2x) (5) + 5² = 2² x² + 20x + 25

= 2² x² + 20x + 25

(2x + 5)² = 4x² + 20x + 25

(ii) (b – 7)²

Comparing (b – 7)² with (a – b)² we have a = b and b = 7

(a – b)² = a² – 2ab + b²

(b – 7)² = b² – 2(b)(7) + 7²

(b – 7)² = b² – 14b + 49

(iii) (mn + 3p)²

Comparing (mn + 3p)² with (a + b)² we have

(a + b)² = a² + 2ab + b²

(mn + 3p)² = (mn)² + 2(mn) (3p) + (3p)²

(mn + 3p)² = m² n² + 6mnp + 9p²

(iv) (xyz – 1)²

Comparing (xyz – l)² with (a – b)² we have = a + xyz and b = 1

 a = xyz and b = 1

(a – b)² = a² – 2ab + b²

(xyz – 1)² = (xyz)² – 2 (xyz) (1) + 1²

(xyz – 1 )² = x²y²z² – 2 xyz + 1

6. Using the identity (a + b)(a − b) = a ² −b² , find the following product.

(i) (p + 2)(p − 2)

(ii) (1 + 3b)(3b − 1)

(iii) (4 − mn)(mn + 4)

(iv) (6x + 7y)(6x – 7y)

Solution:

(i) (p + 2)(p – 2)

Substituting a = p ; b = 2 in the identity (a + b) (a– b) = a² – b², we get

(p + 2)(p – 2) = p² – 2²

(ii) (1 + 3b)(3b – 1)

(1 + 3b) (3b –1) can be written as (3b + 1) (3b –1)

Substituting a = 3b and b = 1 in the identity

(a + b) (a – b) = a² – b², we get

(3b + 1) (3b – 1) = (3b)² – 1² = 3² × b² – 1²

(3b + 1) (3b – 1) = 9b² – 1²

(iii) (4 – mn)(mn + 4)

(4 – mn) (mn + 4) can be written as (4 – mn) (4 + mn) = (4 + mn) (4 – mn)

Substituting a = 4 and b = mn is

(a + b) (a – b) = a² – b², we get

(4 + mn) (4 – mn) = 4² – (mn)² = 16 – m² n²

(iv) (6x + 7y)(6x – 7y)

Substituting a = 6x and b = 7y in

(a + b) (a – b) = a² – b², we get

(6x + 7y) (6x – 7y). = (6x)² – (7y)² = 6²x² – 7²y²

(6x + 7y) (6x – 7y) = 36x² – 49y²

7. Evaluate the following, using suitable identity.

(i) 51²

(ii) 103²

(iii) 998²

(iv) 47²

(v) 297 × 303

(vi) 990 × 1010

(vii) 51 × 52

Solution:  

(i). 51²

 51² = (50+ l)²

 Taking a = 50 and b – 1 we get

 (a + b)² = a² + 2ab + b²

 (50+ l)² = 50² + 2 (50) (1) + 1² = 2500 + 100 +1

 51² = 2601

(ii) 103²

 103² = (100+ 3)²

 Taking a = 100 and b = 3

 (a + b)² = a² + 2ab + b² becomes

 (100+ 3)² = 100² + 2 (100) (3) + 3² = 10000 + 600 + 9

 103² = 10609

(iii) 9982

 998² = (1000–2)²

 Taking a = 1000 and b = 2

 (a – b)² = a² + 2ab + b² becomes

 (1000 – 2)² = 1000² – 2 (1000) (2) + 2²

 = 1000000 – 4000 + 4

 998² = 10,04,004

(iv) 47²

 47² = (50 – 3)²

 Taking a = 50 and b = 3

 (a – b)² = a² – 2ab + b² becomes

 (50 – 3)² = 50² – 2 (50) (3) + 3²

 = 2500 – 300 + 9 = 2200 + 9

 47² = 2209

(v) 297 × 303

 297 × 303 = (300–3) (300+ 3)

 Taking a = 300 and b = 3, then

 (a + b) (a – b) = a² – b² becomes

 (300+ 3) (300–3) = 300² – 3²

 303 × 297 = 90000 – 9

 297 × 303 = 89,991

(vi) 990 × 1010

 990 × 1010 = (1000– 10) (1000+ 10)

 Taking a = 1000 and b = 10 , then

 (a – b) (a + b) = a² – b² becomes

 (1000 – 10) (1000 + 10) = 1000² – 10²

 990 × 1010 = 1000000 – 100

 990 × 1010 = 999900

 (vii) 51 × 52

51 × 52 = (50+ 1) (50 + 2)

Taking x = 50 , a = 1 and b = 2

then (x + a) (x + b) = x² + (a + b) x + ab becomes

(50 +1) (50 + 2) = 50² + (1 + 2) 50 + (l × 2)

= 2500 + (3) 50 + 2 = 2500 + 150 + 2

51 × 52 = 2652

8. Simplify: (a + b)² −4ab

Solution:  (a + b)² – 4ab = a² + b² + 2ab – 4ab = a² + b² – 2ab = (a – b)²

9. Show that (m − n)² +(m + n)² =2(m² +n² )

Solution:

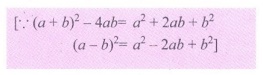
Taking the LHS = (m – n)² + (m + n)²

= m² – 2mn + n² + m² + 2mn + n² = m² + n² + m² + n²

= 2m² + 2n²

= 2(m² + n²) = RHS

∴ (m – n)² + (m + n)² = 2(m² + n²)

10. If a + b =  10 and ab = 18, find the value of a ² +b²

Solution:

We have (a + b)² = a² + 2ab + b²

(a + b)² = a² + b² + 2ab

given a + b = 0 and ab = 18

10² = a² + b² + 2(18)

100 = a² + b² + 36

100 – 36 = a² + b²

a² + b² = 64

11. Factorise the following algebraic expressions by using the identity a ² − b ² =(a + b)(a −b) .

(i) z² − 16

(ii) 9 − 4y²

(iii) 25a² − 49b²

(iv) x ⁴ − y⁴

Solution:

(i) z² – 16

z² – 16 = z² – 4²

We have a² – b² = (a + b) (a – b)

let a = z   and    b = 4,

z² – 4² = (z + 4)(z – 4)

(ii) 9 – 4y²

9 – 4y² = 3² – 2² y² = 3² – (2y)²

let a = 3 and b = 2y, then

a² – b² = (a + b) (a – b)

∴ 3² – (2y)² = (3 + 2y)(3 – 2y)

9 – 4y² = (3 + 2y) (3 – 2y)

(iii) 25a² – 49b²

25a²– 49b² = 5² a² – 7² b² = (5a)² – (7b)²

let A = 5a and B = 7b

A² – B² = (A + B) (A – B) becomes

(5a)² – (7b)² = (5a + 7b)(5a –7b)

(iv) x⁴ – y⁴

Let x⁴ – y⁴ = (x²)² – (y²)²

We have a² – b² = (a + b) (a – b) 

 (x²)² – (y²)² = (x ²+ y²)(x² – y²)

x⁴ – y⁴ = (x² + y²) (x² – y²)

Again we have x² – y² = (x + y) (x – y)

∴ x⁴ – y⁴ = (x² + y²) (x + y) (x – y)

12. Factorise the following using suitable identity.

(i) x² − 8 x +16

(ii) y² + 20y +100

(iii) 36m² + 60m +25

(iv) 64x² − 112xy + 49 y²

(v) a² +6ab + 9b² −c²

Solution:

(i) (i) x² – 8x +16

x² – 8x +16 = x² – (2 × 4 × x) + 4²

This expression is in the form of identity

a² – 2ab + b² = (a – b)²

x² – 2 × 4 × x + 4² = (x – 4)²

x² – 8x + 16 = (x – 4) (x – 4)

(ii) y² + 20y +100

y² + 20y + 100 = y² + (2 × (10))y + (10 × 10)

= y² + (2 × 10 × y) + 10²

This is of the form of identity

a² + 2ab + b² = (a + b)²

y² + (2 × 10 × y) + 10² = (y + 10)²

y² + 20y +100 = (y +10)²

y² + 20y + 100 = (y + 10) (y + 10)

(iii) 36m² + 60m + 25

36m² + 60m + 25 = 6² m² + 2 × 6m × 5 + 5²

This expression is of the form of identity

a² + 2ab + b² = (a + b)²

(6m)² + (2 × 6m × 5) + 5² = (6m + 5)²

36 m² + 60m + 25 = (6m + 5) (6m + 5)

(iv) 64x² – 112xy + 49y²

64x² – 112xy + 49y² = 8² x² – (2 × 8x × 7y) + 7²y²

This expression is of the form of identity

a² – 2ab + b² = (a – b)²

(8x)² – (2 × 8x × 7y) + (7y)² = (8x – 7y)²

64x² – 112xy + 49y² = (8x – 7y) (8x – 7y)

(v) a² + 6ab + 9b² – c²

a² + 6ab + 9b² – c² = a² + 2 × a × 3b + 3² b² – c²

= a² + (2 × a × 3b) + (3b)² – c²

This expression is of the form of identity

[a² + 2ab + b²] – c² = (a + b)² – c²

a² + (2 × a × 3b) + (3b)² – c² = (a + 3b)² – c²

Again this RHS is of the form of identity

a² – b² = (a + b) (a – b)

(a + 3b)² – c² = [(a + 36) + c] [(a + 3b) – c]

a² + 6ab + 9b² – c² = (a +3b + c) (a + 3b – c) 

Objective Type Questions

13. If a + b = 5 and a² + b² =13, then ab = ?

(i) 12

(ii) 6

(iii) 5

(iv) 13

[Answer: (ii) 6]

Solution: (a + b)² = 25

13 + 2ab = 25

       2ab =12

       ab = 6

14. (5 +20)(−20−5)=?

 (i) −425

 (ii) 375

 (iii) −625

(iv) 0

[Answer: (iii) –625]

Solution: (50 + 20) (–20 – 5) = – (5 + 20)² = – (25)² = – 625

15. The factors of x² − 6x +9 are

(i) (x − 3)(x − 3)

(ii) (x − 3)(x + 3)

(iii) (x + 3)(x + 3)

(iv) (x − 6)(x + 9)

[Answer: (i) (x – 3)(x –3)]

Solution: x² – 6x + 9 = x² – 2(x) (3) + 3²

a² – 2ab + b² = (a – b)² = (x – 3)² = (x – 3) (x – 3)

16. The common factors of the algebraic expressions ax² y , bxy² and cxyz is

(i) x² y

(ii) xy²

(iii) xyz

(iv) xy

[Answer: (iv) xy]

Solution: ax²y = a × x × x × y

bxy² = b × x × y × y

cxyz = c × x × y × z

Common factor = xy

Exercise 3.1

1. (i) p²–2pq+q² (ii) x²–25 (iii) (x–2) and (x–2) (iv) 2 × 2 × 2 × 3 × a × b × b × c × c

2. (i) True (ii) False (iii) True (iv) True.

3. (i) 2 × 2 × 2 × 3 × a × b × b × c × c

(ii) 2 × 2 × 3 × 3 × x × x × x × y × y × z

(iii) 2 × 2 × 2 × 7 × m × n × n × p × p

4. (i) x² +10x + 21 (ii) 36a² + 24a – 45 (iii) 16x² + 32xy+15y² (iv) p²q² + 15pq + 56

5. (i) 4x² + 20x + 25 (ii) b² – 14b + 49 (iii) m²n² + 6 mnp + 9p² (iv) x²y²y² – 2 xyz + 1

6. (i) p²– 4 (ii) 9b²–1 (iii) 16 – m²n² (iv) 36x²– 49y²

7. (i) 2, 601 (ii) 10, 609 (iii) 9,96,004 (iv) 2, 209 (v) 89,991 (vi) 9,99,900 (vii) 2,652

8. (a–b)²

10. 64

11. (i) (z + 4) (z – 4) (ii) (3 + 2y) (3 – 2y) (iii) (5a + 7b) (5a – 7b) (iv) (x² + y²) (x + y) (x – y)

12. (i) (x–4) (x–4) (ii) (y + 10) (y + 10) (iii) (6m + 5) (6m + 5) (iv) (8x – 7y) (8x – 7y) (v) (a + 3b + c) (a + 3b – c)

 Objective type questions

13. (ii) 6

14. (iii) – 625

15. (i) (x – 3) (x–3)

16. (iv) xy