Exercise 3.2 (Inequations)

Exercise 3.2

1. Given that x ≥ y. Fill in the blanks with suitable inequality signs.

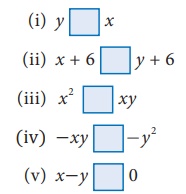
Answer:

(i) y ≤ x

(ii) x + 6 ≥ y + 6

(iii) x²≥ xy

(iv) –xy ≤ – y²

(v) ) x – y   ≥ 0

2. Say True or False.

(i) Linear inequation has almost one solution. [Answer: False]

(ii) When x is an integer, the solutions for x ≤ 0 are −1, −2,... [Answer: False]

(iii) An inequation, −3 < x < −1, where x is an integer, cannot be represented in the number line. [Answer: True]

(iv) x < −y can be rewritten as −y < x [Answer: False]

3. Solve the following inequations.

(i) x ≤ 7, where x is a natural number.

(ii) x − 6 < 1, where x is a natural number.

(iii) 2a + 3 ≤ 13, where a is a whole number.

(iv) 6x − 7 ≥ 35, where x is an integer.

(v) 4x − 9 > −33, where x is a negative integer.

Solution:  

(i) x ≤ 7, where x is a natural number.

Since the solution belongs to the set of natural numbers, that are less than or equal to 7, we take the values of x as 1,2, 3, 4, 5, 6 and 7.

(ii) x – 6 < 1, where x is a natural number.

x – 6 < 1 Adding 6 on the both the sides x – 6 + 6 < 1 + 6

                                                                                x < 7

Since the solutions belongs to the set of natural numbers that are less than 7, we take the values of x as 1,2, 3, 4, 5 and 6

(iii) 2a + 3 ≤ 13, where a is a whole number.

2a + 3 ≤ 13

Subtracting 3 from both the sides

2a + 3 – 3 ≤ 13 – 3

2a ≤ 10

Dividing both the sides by 2.

2a/2 ≤ 10/2

a ≤ 5

Since the solutions belongs to the set of whole numbers that are less than or equal to 5 we take the values of a as 0, 1, 2, 3, 4 and 5

(iv) 6x – 7 ≥ 35, where x is an integer.

6x – 7 ≥ 35 Adding 7 on both the sides

6x –7 + 7 ≥ 35 + 7

6x ≥ 42

Dividing both the sides by 6 we get

6x/6 ≥ 42/6

x ≥ 7

Since the solution belongs to the set of integers that are greater than or equal to 7, we take the values of x as 7, 8, 9, 10...

(v) 4x – 9 > –33, where x is a negative integer.

4x – 9 > – 33 Adding 9 both the sides

4x – 9 + 9 > –33 + 9

4x > – 24

Dividing both the sides by 4

4x/4 > –24/4

x > – 6

Since the solution belongs to a negative integer that are greater than –6, we take values of u as –5, –4, –3, –2 and–1.

4. Solve the following inequations and represent the solution on the number line:

(i) k > −5, k is an integer.

Since the solution belongs to the set of integers, the solution is –4, –3, –2, –1, 0,... It’s graph on number line is shown below.

(ii) −7 ≤ y, y is a negative integer.

–7 ≤ y

Since the solution set belongs to the set of negative integers, the solution is –7,–6,–5,–4,–3,–2,–1.

Its graph on the number line is shown below

(iii) −4 ≤ x ≤ 8, x is a natural number

–4 ≤ x ≤ 8

Since the solution belongs to the set of natural numbers, the solution is 1,2, 3,4, 5, 6, 7 and 8.

Its graph on number line is shown below

(iv) 3m − 5 ≤ 2m + 1, m is an integer.

3m – 5 ≤ 2m + 1

Subtracting 1 on both the sides

3m – 5 – 1 ≤ 2m + 1 + 1

3m – 6 ≤ 2m

Subtracting 2m on both the sides

3m – 6 – 2m ≤ 2m – 2m

m – 6 ≤ 0

Adding 6 on both the sides

m – 6 + 6 ≤ 0 + 6

m ≤ 6

Since the solution belongs to the set of integers, the solution is 6, 5, 4, 3, 2, 1, 0, –1,...

Its graph on number line is shown below 

5. An artist can spend any amount between ₹ 80 to ₹ 200 on brushes. If cost of each brush is ₹ 5 and there are 6 brushes in each packet, then how many packets of brush can the artist buy?

Solution:

Given the artist can spend any amount between ₹ 80 to ₹ 200

Let the number of packets of brush he can buy be x

Given cost of 1 brush = ₹ 5

Cost of 1 packet brush (6 brushes) = ₹5 x 6 = ₹30

∴ Cost of x packets of brushes = 30x

∴ The inequation becomes 80 ≤ 30x ≤ 200

Dividing throughout by 30 we get 80/30  ≤  30x/30  ≤  200/30

8/3 ≤  x  ≤ 20/3 ; 2 (2/3) ≤ x ≤ 6 (2/3)

brush packets cannot get in fractions.

∴ The artist can buy 3 ≤ x ≤ 6 packets of brushes.

or x = 3, 4, 5 and 6 packets of brushes.

Objective Type Questions

6. The solutions of the inequation 3 ≤ p ≤ 6 are (where p is a natural number)

(i) 4, 5 and 6

(ii) 3, 4 and 5

(iii) 4 and 5

(iv) 3, 4, 5 and 6

[Answer: (iv) 3,4,5 and 6]

7. The solution of the inequation 5x + 5 ≤ 15 are (where x is a natural number)

(i) 1 and 2

(ii) 0, 1 and 2

(iii) 2, 1, 0, −1, −2..

(iv) 1, 2, 3..

[Answer: (i) 1 and 2]

Solution: 5x + 5 ≤ 15

5x < 15 – 5 = 10

x ≤ 10/5 = 2 

8. The cost of one pen is ₹ 8 and it is available in a sealed pack of 10 pens. If Swetha has only ₹ 500, how many packs of pens can she buy at the maximum?

(i) 10

(ii) 5

(iii) 6

(iv) 8

[Answer: (iii) 6]

Solution: Price of 1 pen = ₹8

Price of 1 pack = 10 × 8 = 80

Number of packs Swetha can buy = x

80x ≤ 500

8x ≤ 50

x ≤ = 50/8 = 6.25

x is a natural number x = 1, 2, 3, 4, 5, 6

9. The inequation that is represented on the number line as shown below is _______

(i) -4 < x < 0

(ii) −4 ≤ x ≤ 0

(iii) −4 < x ≤ 0

(iv) −4 ≤ x < 0

[Answer: * –4 ≤ x ≤ 2]

ANSWERS:

Exercise 3.2

1. (i) y ≤ x (ii) x + 6 ≥ y + 6 (iii) x² ≥ xy (iv) –xy≤–y² (v) x–y ≥ 0

2. (i) False (ii) False (iii) True (iv) False

3. (i) x = 1, 2, 3, 4, 5, 6 and 7  

  (ii) x = 1, 2, 3, 4, 5 and 6  

  (iii) a = 0, 1, 2, 3, 4 and 5   

 (iv) x = 7, 8, 9, 10, ....

 (v) x = –5, –4, –3, –2 and –1

4. (i) k = – 4, –3, –2, –1, 0, 1, 2, ...

(ii) y = – 7, –6, –5, –4, –3, –2 and –1

(iii) x = 1, 2, 3, 4, 5, 6, 7 and 8

(iv) m = ...–3, -2, –1, 0, 1, 2, 3, 4, 5, 6

5. The artist can buy 3 ≤ x ≤ 6 brushes or x = 3, 4, 5 and 6 brushes.

Objective type questions

 6. (iv) 3, 4, 5 and 6

7. (i) 1 and 2

8. (iii) 6

9. (ii) –4 ≤ x ≤ 0 / –4 ≤ x ≤ 2