Geometric representation of Signals

Geometric representation of Signals:

Derive Geometrical representation of signal.

Basis Vectors

The set of basis vectors {e1, e2, …,en} of a space are chosen such that: Should be complete or span the vector space: any vector a can be expressed as a linear combination of these vectors.

Each basis vector should be orthogonal to all others

·              Each basis vector should be normalized:

·              A set of basis vectors satisfying these properties is also said to be a complete

orthonormal basis

·              In an n-dim space, we can have at most n basis vectors

Signal Space

Basic Idea: If a signal can be represented by n-tuple, then it can be treated in much the same way as a n-dim vector.

Let φ1(t), φ2(t),…., φn(t) be n signals

Consider a signal x(t) and suppose that If every signal can be written as above ⇒ ~ ~ basisfunctions and we have a n-dim signal space

Orthonormal Basis

Signal set {φk(t)}n is an orthogonal set if

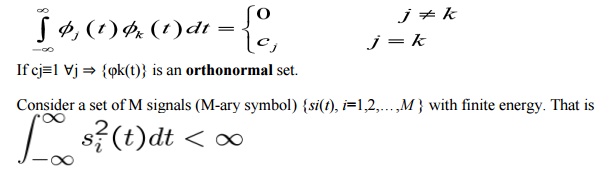
Then, we can express each of these waveforms as weighted linear combination of orthonormal signals

where N ≤ M is the dimension of the signal space and are called the orthonormal basis functions

Let, for a convenient set of {ϕj (t)}, j = 1,2,…,N and 0 ≤ t <T,

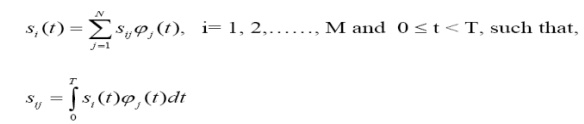
Now, we can represent a signal si(t) as a column vector whose elements are the scalar coefficients

sij, j = 1, 2, ….., N :

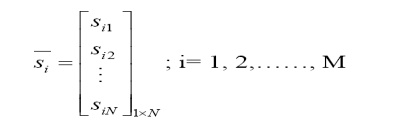
These M energy signals or vectors can be viewed as a set of M points in an N – dimensional

Euclidean space, known as the „Signal Space’.Signal Constellation is the collection of M signals points (or messages) on the signal space