Fluid Statics

FLUID STATICS

Pressure

In fluids we use the term pressure to mean:

The perpendicular force exerted by a fluid per unit area.

This is equivalent to stress in solids, but we shall keep the term pressure. Mathematically, because pressure may vary from place to place, we have:

As we saw, force per unit area is measured in N/m2 which is the same as a pascal

(Pa). The units used in practice vary:

1 kPa       = 1000 Pa  = 1000 N/m2                 

1 MPa = 1000 kPa = 1 × 106 N/m2

1 bar       = 105 Pa= 100 kPa = 0.1 MPa                  

1 atm = 101,325 Pa = 101.325 kPa = 1.01325 bars = 1013.25 millibars For reference to pressures encountered on the street which are often imperial:

1 atm = 14.696 psi (i.e. pounds per square inch) 1 psi = 6894.7 Pa ? 6.89 kPa ? 0.007 MPa

Pressure Reference Levels

The pressure that exists anywhere in the universe is called the absolute pressure, abs P

.This then is the amount of pressure greater than a pure vacuum. The atmosphere onearth exerts atmospheric pressure, atm P , on everything in it. Often when measuringpressures we will calibrate the instrument to read zero in the open air. Any measuredpressure, meas P , is then a positive or negative deviation from atmospheric pressure.We call such deviations a gauge pressure, gauge P . Sometimes when a gauge pressureis negative it is termed a vacuum pressure, vac P .

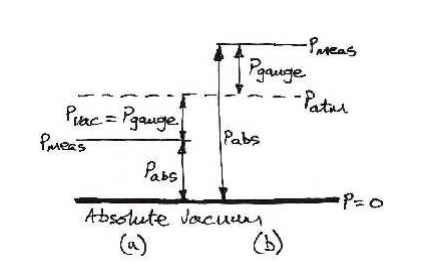
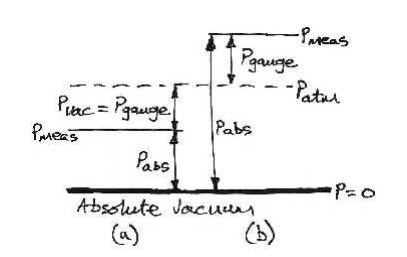
The above diagram shows:

(a)        the case when the measured pressure is below atmospheric pressure and so is a negative gauge pressure or a vacuum pressure;

(b)       the more usual case when the measured pressure is greater than atmospheric pressure by the gauge pressure.

Pressure in a Fluid

Statics of Definition

We applied the definition of a fluid to the static case previously and determined that there must be no shear forces acting and thus only forces normal to a surface act in a fluid. For a flat surface at arbitrary angle we have:

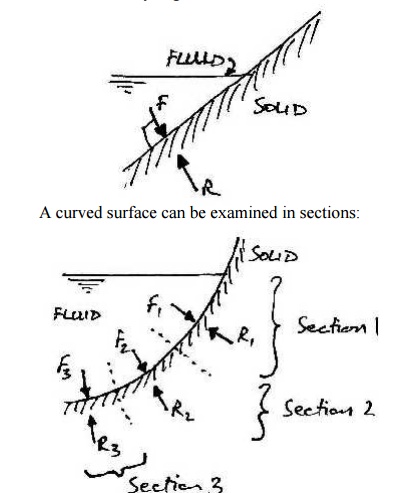
And we are not restricted to actual solid-fluid interfaces. We can consider imaginary planes through a fluid:

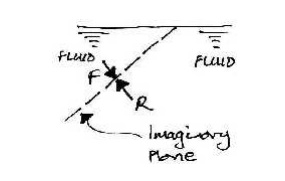
Pascal's Law

This law states:

The pressure at a point in a fluid at rest is the same in all directions.

To show this, we will consider a very small wedge of fluid surrounding the point. This wedge is unit thickness into the page:

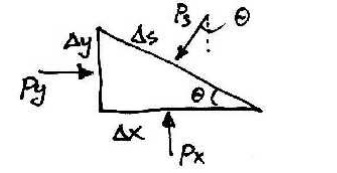
As with all static objects the forces in the x and y directions should balance. Hence:

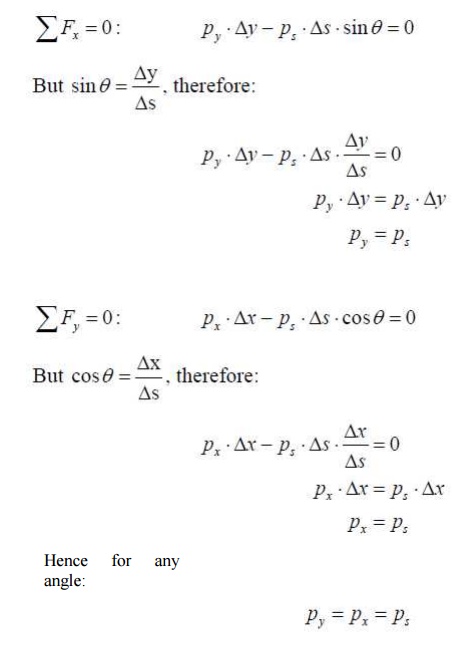
And so the pressure at a point is the same in any direction. Note that we neglected the weight of the small wedge of fluid because it is infinitesimally small. This is why Pascal's Law is restricted to the pressure at a point.

Pressure Variation with Depth

Pressure in a static fluid does not change in the horizontal direction as the horizontal forces balance each other out. However, pressure in a static fluid does change with depth, due to the extra weight of fluid on top of a layer as we move down wards. Consider a column of fluid of arbitrary cross section of area, A:

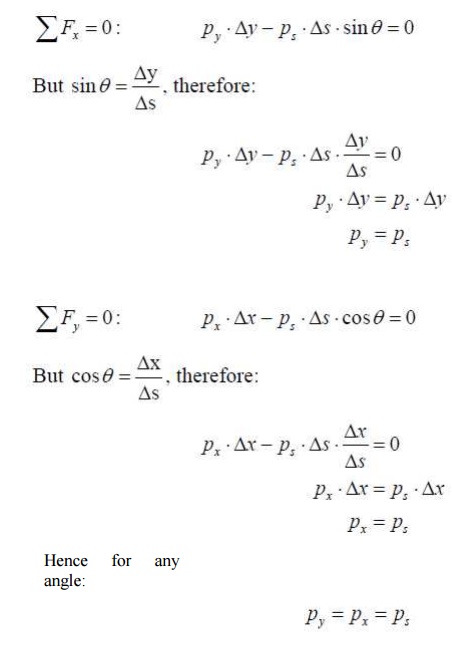
Considering the weight of the column of water, we have:

This difference in pressure varies linearly in h, as shown by the Area 3 of the pressure diagram. If we let h1 = 0 and consider a gauge pressure, then p1 = 0 and we have:

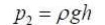
Where h remains the height of the column. For the fluid on top of the column, this isthe source of 1 p and is shown as Area 1 of the pressure diagram. Area 2 of thepressure diagram is this same pressure carried downwards, to which is added more pressure due to the extra fluid.

The gauge pressure at any depth from the surface of a fluid is:

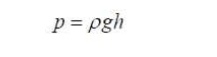
Summary

1.           Pressure acts normal to any surface in a static fluid;

2.           Pressure is the same at a point in a fluid and acts in all directions;

3.           Pressure varies linearly with depth in a

fluid.

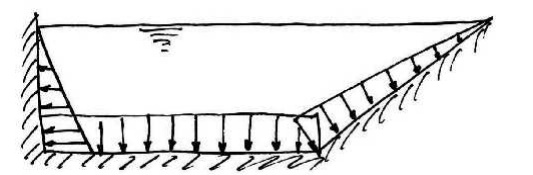
By applying these rules to a simple swimming pool, the pressure distribution around the edges is as shown:

Note:

1.           Along the bottom the pressure is constant due to a constant depth;

2.           Along the vertical wall the pressure varies linearly with depth and acts in the horizontal direction;

3.           Along the sloped wall the pressure again varies linearly with depth but also acts normal to the surface;

4.           At the junctions of the walls and the bottom the pressure is the

same.

Problems - Pressure

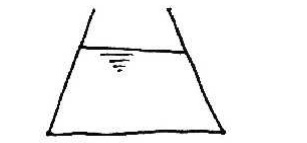
1.           Sketch the pressure distribution applied to the container by the fluid:

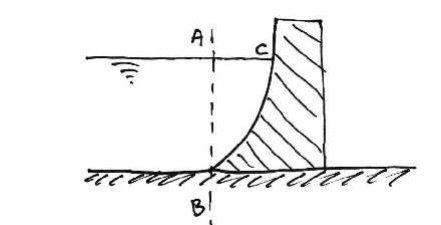
2.           For the dam shown, sketch the pressure distribution on line AB and on the surface of the dam, BC. Sketch the resultant force on the dam.

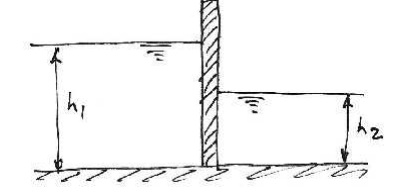
3.           For the canal gate shown, sketch the pressure distributions applied to it. Sketch the resultant force on the gate? If h1 = 6.0 m and h2 = 4.0 m, sketch the pressure distribution to the gate. Also, what is the value of the resultant force on the gate and at what height above the bottom of the gate is it applied

Pressure Head

Pressure in fluids may arise from many sources, for example pumps, gravity, momentum etc.

Since p = ?gh, a height of liquid column can be associated with thepressure p arising from such sources. This height, h, is known as the pressure head.

Example:

The gauge pressure in a water mains is 50 kN/m², what is the pressure head? The pressure head equivalent to the pressure in the pipe is just:

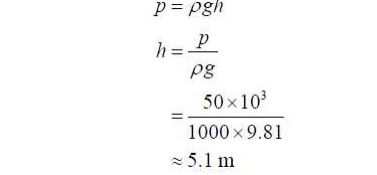
So the pressure at the bottom of a 5.1 m deep swimming pool is the same as the pressure

in this pipe.

Manometers

A manometer (or liquid gauge) is a pressure measurement device which uses relationship

between pressure and head to give readings.

In the following, we wish to measure the pressure of a fluid in a pipe.

Piezometer

This is the simplest gauge. A small vertical tube is connected to the pipe and its top is left open to the atmosphere, as shown.

The pressure at A is equal to the pressure due to the column of liquid of height h1  : Similarly,

The problem with this type of gauge is that for usual civil engineering applications the pressure is large (e.g. 100 kN/m2) and so the height of the column is impractical(e.g.10 m). Also, obviously, such a gauge is useless for measuring gas pressures.

U-tube Manometer

To overcome the problems with the piezometer, the U-tube manometer seals the fluid by

using a measuring (manometric) liquid:

Choosing the line BC as the interface between the measuring liquid and the fluid, we

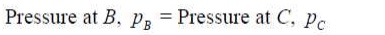
know: For the left-hand side of the U-tube:

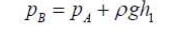
For the right hand side:

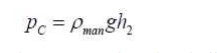
Where we have ignored atmospheric pressure and are thus dealing with gauge pressures. Thus:

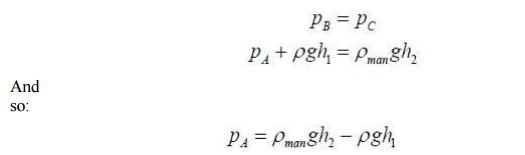
Notice that we have used the fact that in any continuous fluid, the pressure is the same at any horizontal level.

Differential Manometer

To measure the pressure difference between two points we use a u-tube as shown:

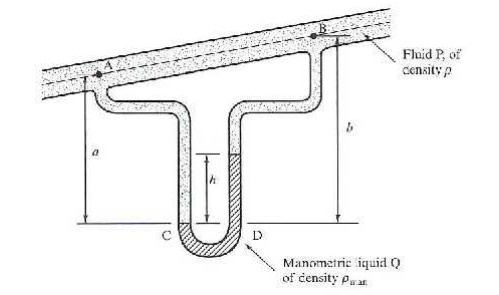
Using the same approach as before:

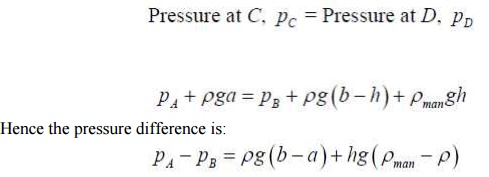
PROBLEM 8

A U-Tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The right limb of the manometer contains water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs U. U tube is 10 cm and the free surface of mercury is in level with over the centre of the pipe. If the pressure of water in pipe line is reduced to 9810 N/m², Calculate the new difference in the level of mercury. Sketch the arrangement in both cases.

Given,

Difference of mercury  = 10 cm = 0.1 m.

Let P_A = pr of water in pipe line (ie, at point A)

The point B and C lie on the same horizontal line. Hence pressure at B should be equal to pressure at C.

But pressure at B = Pressure at A and Pressure due to 10 cm (or) 0.1m of water.

=PA +p ´g ´h

where , P = 1000kg/m³ and h = 0.1 m

=P_A  +1000 ´9.81´0.1

=P_A  +981N / m ²                                        _(i)

Pressure at C = Pressure at D  + pressure due to 10 cm of mercury

0 +P₀ ´g ´h₀

where p_o for mercury   =13.6 ´1000kg / m³

h₀ = 10 cm = 0.1 m

Pressure at C =0 +(13.6 ´1000)´9.81´0.1

= 13341.6 N         (ii)

But pressure at B is = to pr @ c. Hence,

equating  (i) and (ii)

P_A +981 =13341.6

P_A =13341.6 -981 =12360.6N / m ²

II part:

Given  p _A  =9810N / m ²

In this case the pressure at A is 9810 N/m² which is less than the 12360.6 N/m². Hence the mercury in left limb will rise. The rise of mercury in left limb will be equal to the fall of mercury in right limb as the total volume of mercury remains same.

Let, x =  Ries of mercury in left limb in cm

Then fall of mercury in right limb = x cm.

The points B, C and D show the initial condition.

The pressure at B * =  pressure at C*

Pressure at A + pressure due to (10-x) cm of water.

Whereas points B*, C*, and D* show the final conditions.

= pressure at D*  + pressure due to (10-2x) cm of mercury.

(or)

P_A  +p₁ g ´h₁  =pD * +p ₂ ´g ´h₂

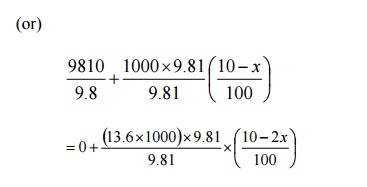
Dividing by 9.81 , we get,

1000 +100 -10x =1360 -272x

272x -10x =1360 -1100

262 x = 260

X=0.992cm

\                                                                New difference of mercury = 10  - 2 x cm

=10 -2 ´0.992

= 8.016 cm.

PROBLEM 9

A differential manometer is connected at the two points A and B of two pipes a shown in figure. The pipe A contains a liquid of sp. Gr = 1.5 while pipe b contains a liquid of sp . gr = 0.9 . The pressures at A and B are 1 kgf / cm² respectively. Find the difference in mercury level in the differential manometer.

Density of mercury   =13.6 ´1000kg / m ³

Pr above  X - X in left limb = 13.6 ´1000 ´9.81´h +1500 ´9.81´(2+3)+P_A

=13.6 ´1000 ´9.81´h +7500 ´9.81´10 ⁴

Pr above X - X in the right limb  =900 ´9.81´(h+2)+P_B

=900´9.81´(h+2)+1.8´10⁴ ´9.81

Equating two pressure, we get,

13.6 ´1000 ´9.81h +7500 ´93.81 +9.81´10 ⁴

=900´9.81´(h+2)+1.8´10⁴ ´9.81

Dividing by  1000 ´9.81,  we get

13.6h +7.5 +10 =(h+2.0)´0.9 +18

13.6h +17.5 =0.9h +1.8 +18 =0.9h +19.8

(13.6 -0.9)h=19.8 -17.5  or  12.7 h = 2.3

h =0.181m =18.1cm