Fluid Properties

INTRODUCTION TO FLUIDS

Definition

There are three states of matter: solids, liquids and gases. Both liquids and gases are classified as fluids.

Fluids do not resist a change in shape. Therefore fluids assume the shape of the container they occupy.

Liquids may be considered to have a fixed volume and therefore can have a free surface.

Liquids are almost incompressible.

C o n v e r s e l y , gases are easily compressed and will expand to fill a container they occupy.

We will usually be interested in liquids, either at rest or in motion.

Definition

The strict definition of a fluid is: A fluid is a substance which conforms continuously

under the action of shearing forces.

To understand this, remind ourselves of what a shear force is:

2 Static Fluids

According to this definition, if we apply a shear force to a fluid it will deform and take up

a state in which no shear force exists. Therefore, we can say: If a fluid is at rest there can be no shearing forces acting and therefore all forces in the fluid must be perpendicular to the planes in which they act. Note here that we specify that the fluid must be at rest. This is because, it is found experimentally that fluids in motion can have slight resistance to shear force. This is

the source of viscosity.

3 Fluids in Motion

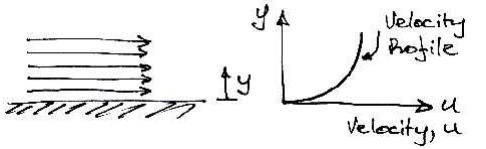
For example, consider the fluid shown flowing along a fixed surface. At the surface there will be little movement of the fluid (it will 'stick' to the surface), whilst furtheraway from the surface the fluid flows faster (has greater velocity):

If one layer of is moving faster than another layer of fluid, there must be shear forcesacting between them. For example, if we have fluid in contact with a conveyor beltthat is moving we will get the behaviour shown:

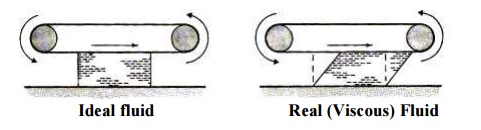
When fluid is in motion, any difference in velocity between adjacent layers has the same effect as the conveyor belt does.

Therefore, to represent real fluids in motion we must consider the action of shear forces

Consider the small element of fluid shown, which is subject to shear force and has a dimension sinto the page. The force F acts over an area A = BC× s. Hence we have a shear stress applied:

Any stress causes a deformation, or strain, and a shear stress causes a shear strain. This shear strain is measured by the angle ? . Remember that a fluid continuously deforms when under the action of shear. This is different to a solid: a solid has a single value of ? for each value of ? . So the longer a shear stress is applied to a fluid, the more shear strain occurs. However, what is known from experiments is that the rate of shear strain (shear strain per unit time) is related to the shear stress:

We need to know the rate of shear strain. From the diagram, the shear strain is:

If we suppose that the particle of fluid at E moves a distance x in time t, then, using S = R? for small angles, the rate of shear strain is:

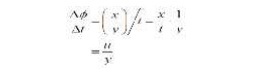
Where u is the velocity of the fluid. This term is also the change in velocity with height. When we consider infinitesimally small changes in height we can write this in differential form, du/ dy . Therefore we have:

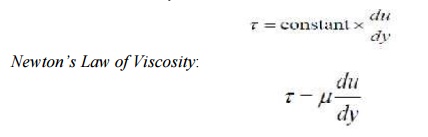
Newton's Law of Viscosity:

Generalized Laws of Viscosity

We have derived a law for the behaviour of fluids - that of Newtonian fluids. However, experiments show that there are non-Newtonian fluids that follow a generalized law of viscosity:

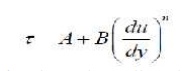
Where A, B and n are constants found experimentally. When plotted these fluids show much different behaviour to a Newtonian fluid:

Behaviour of Fluids and Solids

In this graph the Newtonian fluid is represent by a straight line, the slope of which is ? . Some of

the other fluids are:

Plastic: Shear stress must reach a certain minimum before flow commences.

Pseudo-plastic: No minimum shear stress necessary and the viscosity decreases with rate of shear, e.g. substances like clay, milk and cement.

Dilatant substances; Viscosity increases with rate of shear, e.g. quicksand.

Viscoelastic materials: Similar to Newtonian but if there is a sudden large change in shear they behave like plastic.

Solids: Real solids do have a slight change of shear strain with time, whereas ideal solids (those we idealise for our theories) do not. Lastly, we also consider the ideal

fluid. This is a fluid which is assumed to have no viscosity and is very useful for developing theoretical solutions. It helps achieve some practically useful solutions.

Properties

Further Reading

Here we consider only the relevant properties of fluids for our purposes. Find out about

surface tension and capillary action elsewhere. Note that capillary action only features in

pipes of

? 10 mm diameter.

4. FLUID PROPERTIES:

1.           Density or Mass density: Density or mass density of a fluid is defined as the ratio of the mass of a fluid to its volume. Thus mass per unit volume of a is called density.

Mass density fluid / Mass of  Density of  fluid

The unit of density in S.I. unit is kg/m³. The value of density for water is 1000kg/m

2.Specific weight or weight density: Specific weight or weight density of a fluid is the ratio between the weight of a fluid to its volume. The weight per unit volume of a fluid is called weight density.

Weight density   = Weight of  fluid / Volume of  fluid

w = Mass of  fluid  x g / Volume of  fluid

The unit of specific weight in S.I. units is N/m³. The value of specific weight or weight density of water is

9810N/m³.

3.)Specific Volume: Specific volume of a fluid is defined as the volume of a fluid occupied by a unit mass or volume per unit mass of a fluid.

Specific volume = Volume of  a fluid / Mass of  fluid

Thus specific volume is the reciprocal of mass density. It is expressed as m³/kg. It is commonly applied to gases.

4.)Specific Gravity: Specific gravity is defined as the ratio of the weight density of a fluid to the weight density of a standard fluid.

Specific gravity = Weight density of liquid / Weight density of water

VISCOSITY

Viscosity is defined as the property of a fluid which offers resistance

to the movement of one layer of fluid over adjacent layer of the fluid. When two layers of a fluid, a distance 'dy' apart, move one over the other at different velocities, say u and u+du as shown in figure. The viscosity together with relative velocity causes a shear stress acting between the fluid layers.

COMPRESSIBILITY:

Compressibility is the reciprocal of the bulk modulus of elasticity, K which is defined as the ratio of compressive stress to volumetric strain.

Consider a cylinder fitted with a piston as shown

in figure. Let  V= Volume of a gas enclosed in the

cylinder

P= Pressure of gas when volume is V

Let the pressure is increased to p+dp, the volume of gas decreases

from V to V-dV. Then increase in pressure =dp kgf/m²

Decrease in volume= dV

Volumetric Strain = d / V

- ve sign means the volume decreases with increase of pressure.

Bulk modulus K = Increase pressure / Volumetric Strain

= dp / dV/V

Compressibility is given by = 1/K

Relationship between K and pressure (p) for a Gas:

The relationship between bulk modulus of elasticity (K) and pressure for a gas for two different processes of comparison are as:

(i)          For Isothermal Process: The relationship between pressure (p) and density (?) of a gas as

 ^p = Constant

V  = Constant

Differentiating this equation, we get  (p and V are variables)

PdV +Vdp = 0

or   

pdV= - Vdp      

or

p/dV         = Vdp        

Substituting this value K =p                                      

(ii) For adiabatic process.  For adiabatic process                                   

p    Constant  or         pVk = Constant  

SURFACE TENSION:

Surface tension is defined as the tensile force acting on the surface of a liquid in contact with a gas or on the surface between two two immiscible liquids such that the contact surface behaves like a membrane under tension

CAPILLARITY

Capillarity is defined as a phenomenon of rise or fall of a liquid surface in a small tube relative to the adjacent general level of liquid when the tube is held vertically in the liquid. The rise of liquid surface is known as capillary rise while the fall of the liquid surface is known as capillary depression. It is expressed in terms of cm or mm of liquid. Its value depends upon the specific weight of the liquid, diameter of the tube and surface tension of the liquid.

Problem 1.

Calculate the capillary effect in millimeters a glass tube of 4mm diameter, when immersed in (a) water (b) mercury. The temperature of the liquid is 20⁰ C and the values of the surface tension of water and mercury at 20⁰ C in contact with air are 0.073575 and 0.51 N/m respectively. The angle of contact for water is zero that for mercury 130⁰. Take specific weight of water as 9790 N / m³

Problem 2.

A cylinder of 0.6 m³ in volume contains air at 50⁰C and 0.3 N/ mm² absolute pressure. The air is compressed to 0.3 m³. Find (i) pressure inside the cylinder assuming isothermal process (ii) pressure and temperature assuming adiabatic process. Take K = 1.4

Problem 3

If the velocity profile of a fluid over a plate is a parabolic with the vertex 202 cm from the plate, where the velocity is 120 cm/sec. Calculate the velocity gradients and shear stress at a distance of 0,10 and 20 cm from the plate, if the viscosity of the fluid is 8.5 poise.

Problem 4

A 15 cm diameter vertical cylinder rotates concentrically inside another cylinder of diameter 15.10 cm. Both cylinders are 25 cm high. The space between the cylinders is filled with a liquid whose viscosity is unknown. If a torque of 12.0 Nm is required to rotate the inner cylinder at 100 rpm determine the viscosity of the fluid.

Solution:

Diameter of cylinder = 15 cm = 0.15 m

Diameter of outer cylinder = 15.10 cm  = 0.151 m

Length of cylinder Þ L = 25 cm = 0.25 m

Torque T= 12 Nm ; N = 100 rpm.

Viscosity = m

Problem 5

The dynamic viscosity of oil, used for lubrication between a shaft and sleeve is 6 poise. The shaft is of diameter 0.4 m and rotates at 190 rpm. Calculate the power lost in the bearing for a sleeve length of 90 mm. The thickness of the oil film is 1.5 mm.

Problem 6

If the velocity distribution over a plate is given by u =² y/3 -y ²   in which U is the velocity in m/s at a distance y meter above the plate, determine the shear stress at y = 0 and y = 0.15 m. Take dynamic viscosity of fluid as 8.63 poise.

Problem 7

The diameters of a small piston and a large piston of a hydraulic jack at3cm and 10 cm respectively. A force of 80 N is applied on the small piston Find the load lifted by the large piston when:

·              The pistons are at the same level

·              Small piston in 40 cm above the large piston.

The density of the liquid in the jack in given as 1000 kg/m³

Given:                Dia of small piston  d = 3 cm.