Chapter: Mechanical : Fluid Mechanics And Machinery : Fluid Properties and Flow Characteristics
Fluid Properties and Flow Characteristics
FLUID PROPERTIES AND FLOW CHARACTERISTICS
PRE REQUEST DISCUSSION
This page broadly deal with units and dimensions, properties of fluids and applications of control volume of continuity equation, energy equation, and momentum equation.
Man’s desire for knowledge of fluid phenomena began with his problems of watersupply, irrigation, navigation, and waterpower.
Matter exists in two states; the solid and the fluid, the fluid state being commonly divided into the liquid and gaseous states. Solids differ from liquids and liquids from gases in the spacing and latitude of motion of their molecules, these variables being large in a gas, smaller in a liquid, and extremely small in a solid. Thus it follows that intermolecular cohesive forces are large in a solid, smaller in a liquid, and extremely small in a gas.
DIFFERENCES BETWEEN SOLIDS AND FLUIDS
The differences between the behaviors of solids and fluids under an applied force are as follows:
i. For a solid, the strain is a function of the applied stress, providing that the elastic limit is not exceeded. For a fluid, the rate of strain is proportional to the applied stress.
ii. The strain in a solid is independent of the time over which the force is applied and, if the elastic limit is not exceeded, the deformation disappears when the force is removed. A fluid continues to flow as long as the force is applied and will not recover its original form when the force is removed.
FLUID MECHANICS
Fluid mechanics is that branch of science which deals with the behavior of fluids (liquids or gases) at rest as well as in motion. Thus this branch of science deals with the static, kinematics and dynamic aspects of fluids. The study of fluids at rest is called fluid statics. The study of fluids in motion, where pressure forces are not considered, is called fluid kinematics and if the pressure forces are also considered for the fluids in motion, that branch of science is called fluid dynamics.
UNITS AND DIMENSIONS
The word dimensions are used to describe basic concepts like mass, length, time, temperature and force.Units are the means of expressing the value of the dimension quantitatively or numerically.
Example - Kilogram, Metre, Second, Kelvin, Celcius.
The four examples are the fundamental units; other derived units are
Density = mass per unit volume = kg/m3
Force = mass x acceleration = kg.m/s2 = Newton or N
Pressure = force per unit area = N/m2 =Pascal or Pa
Other unit is‘ bar’ ,
where 1 bar =1 X105 Pa =100 Kpa = 0.1 Mpa
Work = force x distance = Newton x metre = N.m==J or Joule
Power = work done per unit time= J/s = Watt or W
Term Dimension Unit
Area L*L m2
Volume L*L*L m3
Velocity L* T-1 m/s
Acceleration L*T-2 m/s2
Force M*L*T-2 N
Pressure M*L-1*T-2 N/m2 = Pa
Work M*L2*T-2 Nm = J
Power M*L2*T-3 J/s = W
Density M*L-3 kg/m3
Viscosity M*L-1*T-1 kg/ms = N s/m2
Surface Tension M*T-1 N/m
Quantity Representative symbol Dimensions
Angular velocity w t-1
Area A L2
Density r M/L3
Force F ML/t2
Kinematic viscosity n L2/t
Linear velocity V L/t
Linear acceleration A L/t2
Mass flow rate m. M/t
Power P ML2/t3
Pressure P M/Lt2
Sonic velocity C L/t
Shear stress t M/Lt2
Surface tension s M/t2
Viscosity m M/Lt
Volume V L3
Dimensions:
Dimensions of the primary quantities:
Fundamental dimension : Symbol
Length L
Mass M
Time T
Temperature T
Dimensions of derived quantities can be expressed in terms of the fundamental dimensions.
1.SYSTEM OF UNITS
1. CGS Units
2. FPS Units
3. MKS Units
4. SI Units
FLUID PROPERTIES
1 Density or Mass density:
Density or mass density of a fluid is defined as the ratio of the mass of a fluid to its volume. Thus mass per unit volume of a is called density.
2. Specific weight or weight density:
Specific weight or weight density of a fluid is the ratio between the weight of a fluid to its volume. The weight per unit volume of a fluid is called weight density.
3. Specific Volume:
Specific volume of a fluid is defined as the volume of a fluid occupied by a unit mass orvolume per unit mass of a fluid
4.Specific Gravity:
Specific gravity is defined as the ratio of the weight density of a fluid to the weight density of a standard fluid.
VISCOSITY
Viscosity is defined as the property of a fluid which offers resistance to the
movement of one layer of fluid over adjacent layer of the fluid. When two layers of a fluid, a distance ‘dy’ apart, move one over the other at different velocities, say u
and u+du as shown in figure. The viscosity together with relative velocity causes a shear stress acting between the fluid layers
The top layer causes a shear stress on the adjacent lower layer while the lower layer causes a shear stress on the adjacent top layer. This shear stress is proportional to the rate of change of velocity with respect to y.
VAPOUR PRESSURE
The pressure at which a liquid will boil is called its vapor pressure. This pressure is a function 3 of temperature (vapor pressure increases with temperature). In this context we usually think about the temperature at which boiling occurs. For example, water boils at 100oC at sea-level atmospheric pressure (1 atm abs). However, in terms of vapor pressure, we can say that by increasing the temperature of water at sea level to 100 oC, we increase the vapor pressure to the point at which it is equal to the atmospheric pressure (1 atm abs), so that boiling occurs. It is easy to visualize that boiling can also occur in water at temperatures much below 100oC if the pressure in the water is reduced to its vapor pressure. For example, the vapor pressure of water at 10oC is 0.01 atm.
1.CAVITATION
Cavitation(flashing of the liquid into vapour) takes place when very low pressures are produced at certain locations of a flowing liquid. Cavitation results in the formation of vapour pockets or cavities which are carried away from the point of origin and collapse at the high pressure zone.
COMPRESSIBILITY
Compressibility is the reciprocal of the bulk modulus of elasticity, K which is defined as the ratio of compressive stress to volumetric strain.
Compressibility is given by = 1/K
SURFACE TENSION
Surface tension is defined as the tensile force acting on the surface of a liquid in contact with a gas or on the surface between two two immiscible liquids such that the contact surface behaves like a membrane under tension.
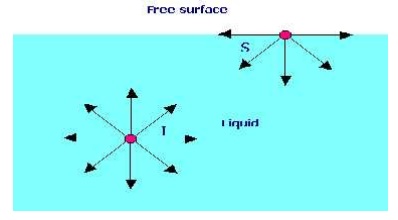
1.A soap bubble 50 mm in diameter contains a pressure (in excess of atmospheric) of 2 bar. Find the surface tension in the soap film.
Data:
Radius of soap bubble (r) = 25 mm = 0.025 m Dp = 2 Bar = 2 x 105 N/m2
Formula:
Pressure inside a soap bubble and surface tension (s) are related by, Dp = 4s/r
Calculations:
s = Dpr/4 = 2 x 105 x 0.025/4 = 1250 N/m
CAPILLARITY
Capillarity is defined as a phenomenon of rise or fall of a liquid surface in a small tube relative to the adjacent general level of liquid when the tube is held vertically in the liquid. The rise of liquid surface is known as capillary rise while the fall of the liquid surface is known as capillary depression.
It is expressed in terms of cm or mm of liquid. Its value depends upon the specific weight of the liquid, diameter of the tube and surface tension of the liquid.
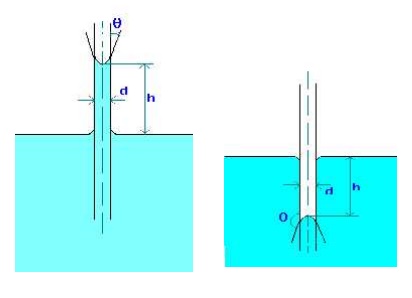
1.Water has a surface tension of 0.4 N/m. In a 3 mm diameter vertical tube if the liquid rises 6 mm above the liquid outside the tube, calculate the contact angle.
Data:
Surface tension (s) = 0.4 N/m
Dia of tube (d) = 3 mm = 0.003 m
Capillary rise (h) = 6 mm = 0.006 m
Formula:
Capillary rise due to surface tension is given by
h = 4 cos(q)/(rgd), where q is the contact angle.
Calculations:
cos(q) = hrgd/(4s) = 0.006 x 1000 x 9.812 x 0.003 / (4 x 0.4) = 0.11
Therfore, contact angle q = 83.7o
CONCEPT OF CONTROL VOLUME
A specified large number of fluid and thermal devices have mass flow in and out of a system called as control volume.
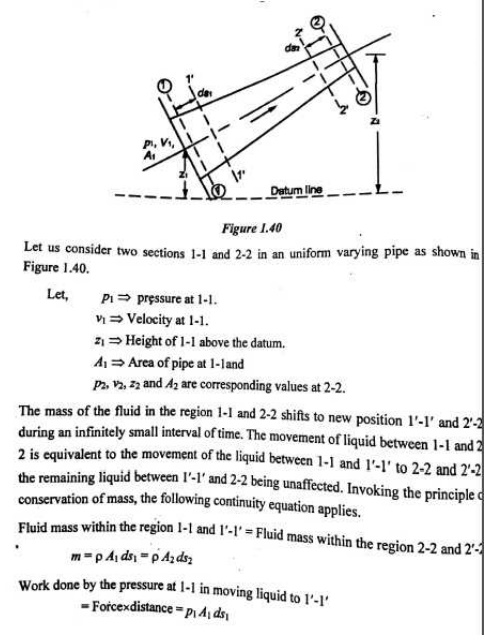
1.CONTINUITY EQUATION
Concepts
The continuity equation is governed from the principle of conservation of mass.It states that the mass of fluid flowing through the pipe at the cross-section remains constants,if there is no fluid is added or removed from the pipe.
Let us make the mass balance for a fluid element as shown below: (an open-faced cube)
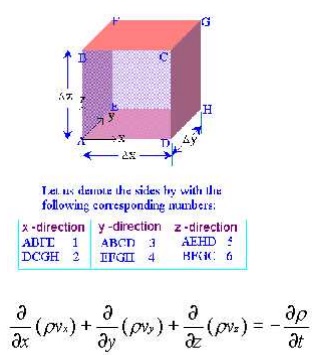
This is the continuity equation for every point in a fluid flow whether steady or unsteady , compressible or incompressible.
For steady, incompressible flow, the density r is constant and the equation simplifies to
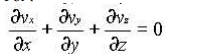
For two dimensional incompressible flow this will simplify still further to
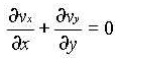
2 EULER'S EQUATION OF MOTION

This is known as Euler's equation, giving, in differential form the relationship between p, v, rand elevation z, along a streamline for steady flow.
3 BERNOULLI EQUATION
Concepts
Bernoulli’s Equation relates velocity, pressure and elevation changes of a fluid in motion. Itmay be stated as follows “ In an ideal incompressible fluid when the flow is steady and
continuous the sum of pressure energy, kinetic energy and potential energy is constant along streamline”
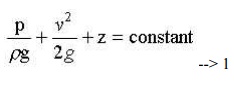
This is the basic from of Bernoulli equation for steady incompressible inviscid flows. It may be written for any two points 1 and 2 on the same streamline as
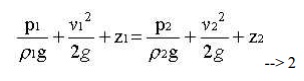
The contstant of Bernoulli equation, can be named as total head (ho) has different values on different streamlines.
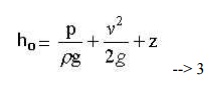
The total head may be regarded as the sum of the piezometric head h* = p/rg + z and the kinetic head v2/2g.
Bernoullie equation is arrived from the following assumptions:
1. Steady flow - common assumption applicable to many flows.
2. Incompressible flow - acceptable if the flow Mach number is less than 0.3.
3. Frictionless flow - very restrictive; solid walls introduce friction effects.
4. Valid for flow along a single streamline; i.e., different streamlines may have different ho.
5. No shaft work - no pump or turbines on the streamline.
6. No transfer of heat - either added or removed.
Range of validity of the Bernoulli Equation:
Bernoulli equation is valid along any streamline in any steady, inviscid, incompressible flow. There are no restrictions on the shape of the streamline or on the geometry of the overall flow. The equation is valid for flow in one, two or three dimensions.
Modifications on Bernoulli equation:
Bernoulli equation can be corrected and used in the following form for real cases.
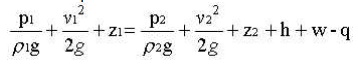
APPLICATIONS
1.Venturimeter.
2.Orificemeter
3.Pitot Tube
MOMENTUM EQUATION
Net force acting on fluid in the direction of x=Rate of change of momentum in x direction
=Mass per sec×Change in velocity
p1A1-p2A2×cos θ-Fx=ρQ(v2cosθ-v1)
Fx=ρQ(v1-v2cosθ)-p2A2cosθ+p1A1
Similarlt,the momentum in y-direction is -p2A2sinθ+Fy=ρQ(v2sinθ-0)
Fy=ρQv2sinθ+p2A2 sinθ
Resultant force acting on the bend,
Fr=√Fx²+Fy²
GLOSSARY
Quantity : Unit
Mass in Kilogram : Kg
Length in Meter : M
Time in Second : s or as sec
Temperature in Kelvin : K
Mole : gmol or simply as mol
Derived quantities:
Quantity : Unit
Force in Newton (1 N = 1 kg.m/s2) : N
Pressure in Pascal (1 Pa = 1 N/m2) : N/m2
Work, energy in Joule ( 1 J = 1 N.m) : J
Power in Watt (1 W = 1 J/s) : W


















Related Topics