Flow Net (Soil Water)

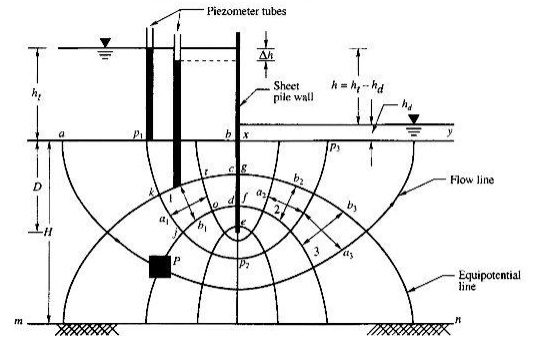
FLOW NET (Soil Water)

A flow net for an isometric medium is a network of flow lines and equipotential lines intersecting at right angles to each other. The path which a particle of water follows in its course of seepage through a saturated soil mass is called a flow line. Equipotential lines are lines that intersect the flow lines at right angles. At all points along an equipotential line, the water would rise in piezometric tubes to the same elevation known as the piezometric head .

1 LAPLACE EQUATION:

Laplace equation for two dimensional flows. Assumption

1. The saturated porous medium is compressible. The size of the pore space doesn't change with time, regardless of water pressure.

2.  The seeping water flows under a hydraulic gradient which is due only to gravity head loss, or Darcy's law for flow through porous medium is valid.

3.  There is no change in the degree of saturation in the zone of soil through which water seeps and quantity of water flowing into any element of volume is equal to the quantity which flows out in the same length of time.

4.  The hydraulic boundary conditions of any entry and exit are known

5.   Water is incompressible. Consider an element of soil of size ?x, ?y and of unit thickness perpendicular to the plane of the paper Let Vx and Vy be the entry velocity components in X and Y directions.

Then (Vs) + (dVx/dx)

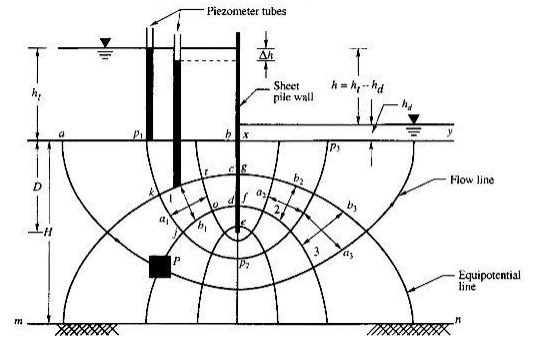
The figure represents a section through an impermeable diaphragm extending to a depth below the horizontal surface of a homogeneous stratum of soil of depth H. It is assumed that the difference h between the water levels on the two sides of the diaphragm is constant. The water enters the soil on the upstream side of the diaphragm, flows in a downward direction and rises on the downstream side towards the surface. Consider a

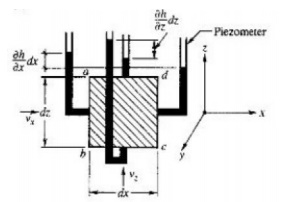
prismatic element P shown shaded in Fig.2.8 which is shown on a larger scale in 2.9. The element is a parallelepiped with sides' dx, dy and dz. The x and z directions are as shown in the figure and the y direction is normal to the section. The velocity v of water which is tangential to the stream line can be resolved into components vx and vz in the x and z directions respectively.

ic= ?(??)/(?x) the hydraulic gradient in the horizontal direction.

iz= ?(? ?)/(? z) the hydraulic gradient in the vertical direction.

kx = hydraulic conductivity in the horizontal direction. kz = hydraulic conductivity in the vertical direction.

If we assume that the water and soil are perfectly incompressible, and the flow is steady, then

the quantity of water that enters the element must be equal to the quantity that leaves it.

The quantity of water that enters the side ab=vxdzdy

The quantity of water that leaves the side cd = vx +(?vx/ ?x )dx dy dz

The quantity of water that enters the side bc = vzdxdy                                     

The quantity of water that leaves    side ad = vz+ (?vz/?z)dz dxdy

Therefore, we have the equation,

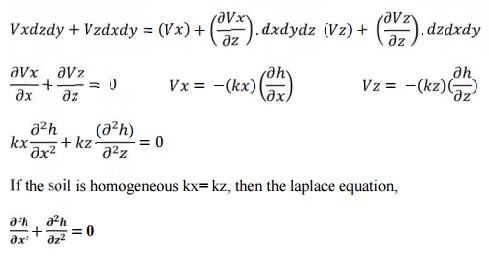
2 Flow net Construction:

The graphical method of flow net construction, first given by Forchheimer (1930), is based on trial sketching. The hydraulic boundary conditions have a great effect on the general shape of the flow net, and hence must be examined before sketching is started The flow net can be plotted by trial and error by observing the following properties of flow net and by following the practical suggestions given by A. Casagrande.

3 Properties of flow net.

The flow lines and equipotential lines meet at right angles to one another.

The fields are approximately squares, so that a circle can be drawn touching all the four sides of the square.

The quantity of water flowing through each flow channel is the same. Simiary, the same potential drop occur between two successive equipotential lines.

Smaller the dimensions of the field, greater will be the hydraulic gradient and velocity of flow through it.

In a homogeneous soil, every transition in the shape of the curves is smooth, being either elliptical or parabolic in shape.

4 Hints to draw flow net:

Use every opportunity to study the appearance of well constructed flow nets. When the picture is sufficiently absorbed in your mind, try to draw the same flow net without looking at the available solution ; repeat this until you are able to sketch this flow net in a satisfactory manner.

Four or five flow channels are usually sufficient for the first attempts ; the use of too many flow channels may distract the attention from essential features.

Always watch the appearance of the entire flow net. Do not try to adjust details before the entire flow net is approximately correct.

The beginner usually makes the mistake of drawing too sharp transitions between straight and curved sections of flow lines or equipotential lines. Keep in mind that all transitions are smooth, of elliptical or parabolic shape. The size of the squares in each channel will change gradually.

5 FLOW NET FOR VARIOUS WATER RETAINING STRUCTURES

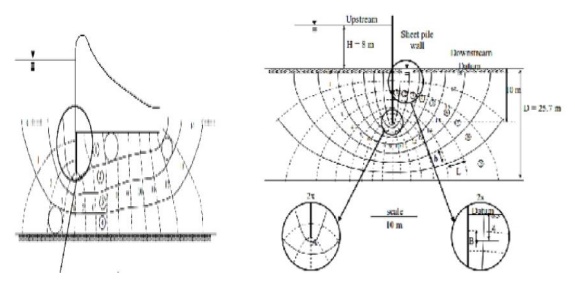
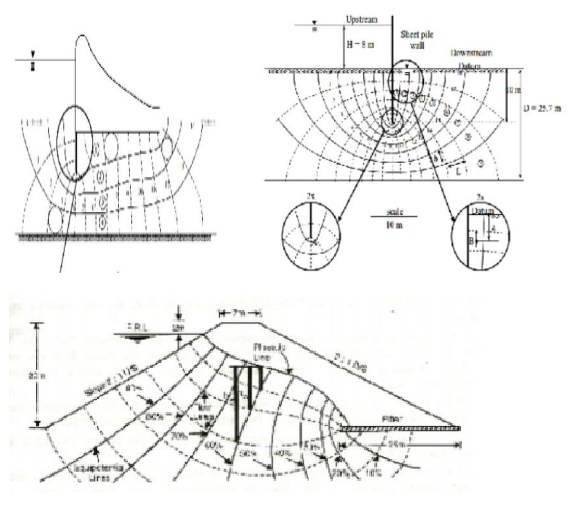
6 Flow net can be utilized for the following purposes:

Determination of seepage, Determination of hydrostatic pressure, Determination of seepage pressure, Determination of exit gradient

i. Determination of seepage

The portion between any two successive flow lines is at flow channel. The portion _?enclosed two successive equipotential lines and successive flow lines are known as field. _?Let b and l be the width and length of the field.

h = head drop through the field

q = discharge passing through the flow channel

H = Total hydraulic head causing flow = difference between upstream and downstream weeds.

ii.Determination of hydrostatic pressure.

The hydrostatic pressure at any point within the soil mass is given by u  =  h w?w

Where, u = hydrostatic pressure

hw = Piezometric head.

The hydrostatic pressure in terms of  piezometric head  hw  is calculated from the following relation.

h w =  h- z

iii.Determination of seepage pressure

The hydraulic potential h at any point located after N potential drops, each of value

given by b ?H = E?h

The seepage pressure'of any point the hydraulic potential or the balance hydraulic head multiplied by the unit

Weight of water, Ps h?w.?Hh

The pressure acts in the direction flow

iv.Determination of exit ?gradient.

The exit gradient is the hydraulic gradient of the downstream end of the flow line where

the  percolating  water  leaves  the  soil  mass  and  emerges  into  free  water  at  the

downstream.The exit gradient can be calculated from the following expression, in

h represents the potential drop and l the average length of last field in the flow

exit end.

ie=?h/L