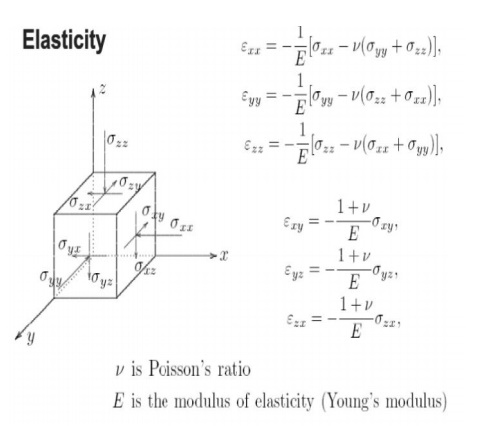
The Principle Of Effective Stress

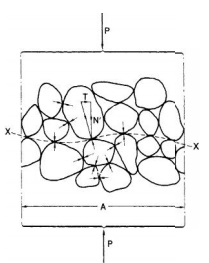
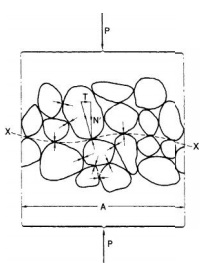
STRESS DISTRIBUTION AND SETTLEMENT

A soil can be visualized as a skeleton of solid particles enclosing continuous voids which contain water and/or air. For the range of stresses usually encountere d in practice the individual solid particles and water can be considered incompressible; air, on the other hand, is highly compressible. The volume of the soil skeleton as a whole can change due to rearrangement of the so il particles into newpositions, mainlyby ro lling and sliding, with a corresponding change in the forces acting between particles. The actual compressibility of the soil skeleton will depend on the structural arrangeement of the solid particles. In a fully satura ted soil, since water is considered to be i ncompressible, a reduction in volume is pos sible only if some of the water can escape fro m the voids. In a dry or a partially saturated soil a reduction in volume is always possible due to compression of the air in t he voids, provided there is scope for partic le rearrangement. Shear stress can be resisted only by the skeleton of solid particles, by means of forces developed at the interpartic le contacts. Normal stress may be resisted by the soil skeleton through an increase in the interparticle forces. If the soil is fully saturated, the water filling the voids can also withstand normal stress by an increase in pressure.

THE PRINCIPLE OF EFFECTIVE STRESS      

The  importance  of  the  fo rces  transmitted  through  the  soil       skeleton  from      particle  to particle was  recognized i n 1923 when Terzaghi presented          the principle of effective  stress, an intuitive relations hip based on experimental data. The principle applies only to fully saturated soils and relates the following three stresses:

1.The total normal stress (      ) on a plane within the soil mass, being the force per unit area transmitted in a normal d irection across the plane, imagining the s oil to be a solid (single-phase) material;

2 the pore water pressure        (u), being the        pressure of  the water     fillin g the void space between the solid particles;

3 the effective normal stress ( ) on the plane, representing the stress transmitted through the soil skeleton only.

The relationship is:

The principle can be repres ented by the following physical model. Con sider a 'plane XX in a fully saturated soil, passing through points of interparticle contact only, as shown in Figure. The wavy plane X X is really indistinguishable from a true plane on the mass scale due to the relatively small size of individual soil particles. A normal force P applied over an area A may be resisted partly by interparticle forces and partly by the pressure in the pore water. The interparticle forces are very random in both magnitude and direction throughout the soil mass but at every point of contact on the wavy p lane may be split into components normal and tangential to the direction of the true plane to which XX approxi mates; the normal and tangential components are N' and T, respectively.

Then, the effective normal stress is interpreted as the sum of all the components N' within th e area A, divided by the area A, i.e.

The total normal stress is given by If point contact is assumed between the particles, the pore water pressure will act on the plane over the entire area A.

Then, for equilibrium in the direction normal to XX

p= ?N' + uA

s=s'+u

The pore water pressure which acts equally in every direction will act on the entire surface of any Particle but is assumed not to change the volume of the particle; also, the pore water pressure does not cause particles to be pressed together. The error involved in assuming point contact between particles is negligible in soils, the total contact area normally being between 1 and 3% of the cross-sectional area A. It should be understood that N'does not represent the true contact stress between two particles, which would be the random but very much higher stress N', where a is the actual contact area between the particles.

2 Effective vertical stress due to self-weight of soil                                  

Consider soil mass having a horizontal surface and with the water table at surface level. The total vertical stress (i.e. the total normal stress    on a horizontal plane) at  depth z is equal to the weight of all material (solids þ water) per unit area above that

sv = rsat z

The pore water pressure at any depth will be hydrostatic since the void space between the solid particles is continuous, so at depth z u = rwz Hence, from Equation is the effective vertical stress at depth z will be

s = (gsat - gw)z = gz where g is the buoyant unit weight of the soil.

3 RESPONSE OF EFFECTIVE STRESS TO A CHANGE IN TOTAL STRESS

As an illustration of how effective stress responds to a change in total stress, consider the case of a fully saturated soil subject to an increase in total vertical stress and in which the lateral strain is zero, volume change being entirely due to deformation of the soil in the vertical direction. This condition may be assumed in practice when there is a change in total vertical stress over an area which is large compared with the thickness of the soil layer in question. It is assumed initially that the pore water pressure is constant at a value governed by a constant position of the water table. This initial value is called the static pore water pressure (us). When the total vertical stress is increased, the solid particles immediately try to take up new positions closer together. However, if water is incompressible and the soil is laterally confined, no such particle rearrangement, and therefore no increase in the inter particle forces,is possible unless some of the pore water can escape. Since the pore water is resisting the particle rearrangement the pore water pressure is increased above the static value immediately theincrease in total stress takes place.The increase in pore water pressure will be equal to the increase in total vertical stress, i.e. the increase in total vertical stress is carried entirely by the pore water. Note that if the lateral strain were not zero some degree of particle rearrangement would be possible, resulting in an immediate increase in effective vertical stress and the increase in pore water pressure would be less than the increase in total vertical stress. The increase in pore water pressure causes a pressure gradient, resulting in a transient flow of pore water towards a free-draining boundary of the soil layer. This flow or drainage will continue until the pore water pressure again becomes equal to the value governed by the position of the water table.

The component of pore water pressure above the static value is known as the excess pore water pressure (ue). It is possible, however, that the position of the water table will have changed during the time necessary for drainage to take place, i.e. the datum against which excess por e water pressure is measured will have changed.

In such cases the excess pore water pressure should be expressed wit h reference to the static value governed by the new water table position. At any time du ring drainage the overall pore water pressure (u) is equal to the sum of the static and excess components, i.e.

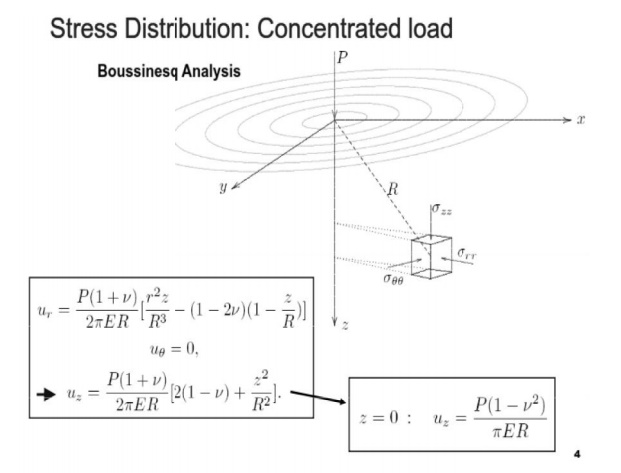
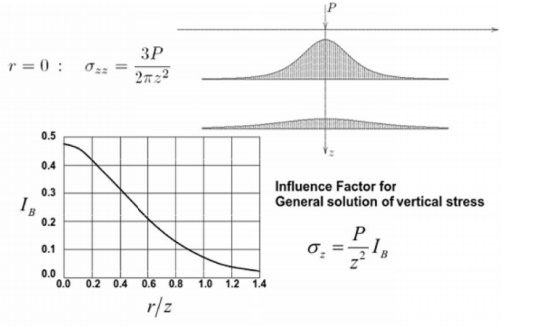
3.2.1 Vertical Concent ration Load