Financial and economic feasibility of investment - Aquaculture

Financial and economic feasibility of investment

Being a new industry, it has not always been easy to obtain financing for commercial-type aquaculture. Financing has become particularly difficult because of the failure of a number of badly planned projects. The longer gestation periods of aquaculture projects have added to these problems, even though the export potential of some types of farming has created considerable private and public sector interest. Experience so far clearly points to the need for appropriate feasibility studies of investments to enable informed decision-making and avoidance of unforeseen failures.

The major sources of financing for large-scale aquaculture projects presently appear to be owner’s equity and institutional financing, or a combination of both. Socially oriented small-scale projects may often be financed partially or wholly from public-sector resources. Criteria for decisionmaking for investments will naturally depend on the source and terms of financing, but the need for financial or economic feasibility analysis is equally applicable for all projects.

Among the many methods available for feasibility studies, the most widely used ones for appraisal and comparison in aquaculture are the pay-back period, the average rate of return and discounting or present value (Shang, 1981). The last method (which includes the net present value, the internal rate of return and the benefit-cost ratio) is considered the most useful means of assessing the economic feasibility of an investment.

The pay-back period is sometimes referred to as simply an estimate of the time required to recover the initial investment out of the expected earnings from the investment, before any allowance for depreciation. It does not take into account profits realized after the recovery of the initial investment recovery period and the timing of expenditures and income. However, it helps an investor to have some assurance of the recovery of his capital in a risky venture, though it will not help him to assess the merits of the investment in relation to other investment opportunities that may exist.

The average rate of return is the average annual profits expected after depreciation divided by the project’s initial investment:

Average annual rate of return = Average annual profit expected after depreciation / Initial investment

This method permits comparison of return on investment with other possible investments in projects having similar expenditure and earning profiles. But it does not take into account the timings of expenditure and earnings. A good part of the capital outlays is made in the beginning of an aquaculture project and incomes may take some time to build up, but will continue for long periods.These timings are of crucial importance in judging the feasibility of the venture.

The discounting method or present-value method takes this aspect into full account and provides a better indication of the advisability of the investment. This method is based on the concept that the value of an investment today is much greater than its future value. In the normal course of events, a sum of money, if invested or loaned today, will start earning interest and, with reinvestment, can be expected to increase as a function of time. If a sum P0 is loaned at an interest rate of r for n years, at the end of thenth year it can be expected to have the value Pn = P0 (1 = r)n. Today’s value of Pn can be found by solving:

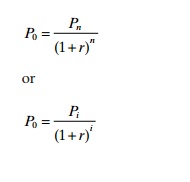
where i is the number of years in operation. The present value of any series of future cash out-flows and inflows can be determined by the above formulae. Pre-calculated tables are available for the present value of a dollar received or spent at one point in time for 50 years (1 + r)n, and the present value of a dollar received annually at the end of each year at various discount rates [1 - (1 + r)n]/r. So it will not be necessary to calculate the value every time.

Financial analysis

The financial analysis of commercial aquaculture projects, as well as the economic analysis of socially oriented aquaculture projects, can be carried out by using the discounting method. The data required are very similar to the ones used in the evaluation of farm performance. These data should be as realistic as possible and preferably based on actual experience in the area. Inflation and relative price changes in the future should be considered. If the total capital investment (including owner’s equity and borrowed capital) is treated as an initial cost of the project, depreciation and interest on borrowed capital should not be included in the annual operating cost, to avoid double counting. In case the owner’s equity is treated as an initial cost, the amount of borrowed credit should be treated as an income at the time of borrowing. The payment of the principal and the interest on borrowed capital should then be included as operating costs. The annual cost of the loan (principal and interest) can be calculated using the amortization formula:

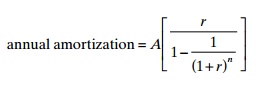
where

A =the amount of the loan

r =the interest rate

n =duration of the loan (in years)

Net present value method

One way to assess the feasibility of an investment project by the discounting method is by the use of the net present value. This is done by subtracting the costs from the returns (benefits) on a year-to-year basis to arrive at the net profit (or benefit) stream, which is then discounted into a present value estimate as shown in the equation below:

As an example, the net present value of net benefit (income) of a hypothetical project is given in Table 13.7. The net present value can also be calculated by discounting independently the stream of annual cash flow (B) and cash outflow (C) and subtracting the sum of the latter from that of the former as shown below:

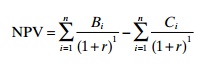
If the NPV is more than 0, the investment will be profitable; if it is less than 0, it will not be profitable. If the NPV is equal to 0, it will be a break-even situation.

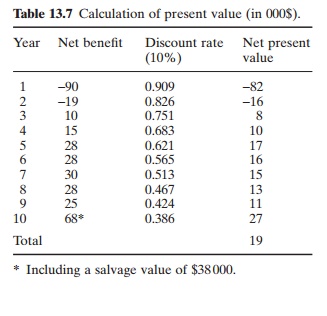
The most appropriate rate of discount for calculations is the opportunity cost of the capital, and there are practical problems in establishing this rate. As it is not possible to determine the appropriate rate at the project level, it will be necessary to obtain it from a central planning agency.

Benefit-cost ratio

The benefit-cost ratio is defined as the ratio of the present total value of the benefits to the cost. This method is more appropriate to determine the social and economic worth of a project. The net and gross benefit-cost ratios can be estimated as follows:

where

B = the net annual benefit (income)

K = the capital outlay for assets

R = the gross annual benefit or income

C = the annual operating cost

An example of the benefit-cost ratio calculation is shown in Table 13.8. The gross benefit ratio at 10 per cent discount will be 375/355 = 1.06. An investment with a benefit-cost ratio greater than 1 can be considered as feasible. The problem of choosing an appropriate rate of discount is encountered in this type of analysis as well.

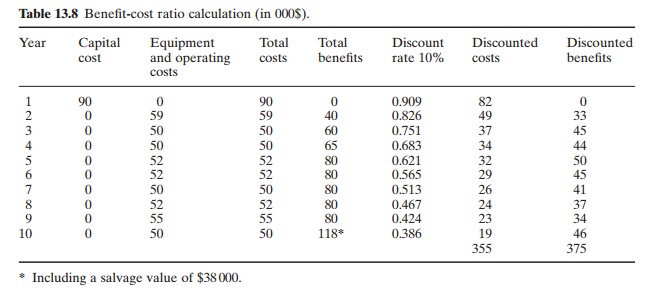
Internal rate of return

The internal rate of return of an investment (K) is the discount rate that makes the present value of the net cash inflow equal to zero. The difficulties of choosing an appropriate discount rate encountered in the earlier two methods (net present value and benefit-cost ratio) can be avoided to a considerable extent. If the benefit (or incomes) and costs are known, it can be solved by setting the left-hand side of the net present value formula (see previous page) equal to zero.

This represents the average earning power of money used in the project over the project’s life. It can be calculated by computing the rate of return on investment or the return on equity. If the total capital outlay is treated as investment, K is the internal rate on investment. On the other hand, if the owner’s equity is treated as the initial investment, K is the internal rate of return on equity. Thus K can be a measure for comparing returns on other investment opportunities.

The appropriate rate of discount has to be found through a process of trial and error. By trying several rates, a close approximation can be reached. When the calculated discount rates are positive, a higher discount rate has to be used. If the result is negative, a lower discount rate should be used. To shorten the trialand-error computations and find an approximate discount rate, the following method can be used. Divide the capital cost by the average expected annual net income (if relatively stable over time). From the precalculated tables of present values (Shang, 1981) it will be found that the result of the division lies in a range of discount rates at a given analysis period. The internal rate of return (IRR) can then be inter-polated by the following method (Gittinger, 1972; Shang, 1981):

As an example, Table 13.9 sets forth the inter-nal rate of return on a $110000 investment, with an expected annual average profit of about $23200 for 10 years (after the first two years). To find the first approximate discount rate, the capital cost is divided by the average expected annual income: 110000/23 200 = 4.74. This discount

factor lies between 16 and 17 per cent at year 10, according to the table of precalculated present values.Taking this as a starting point for trial-and-error computation, the present value of net income (benefit) is -11, at 16 per cent, which indicates that the discount rate used is too high, and it is 14 at 11 per cent, which indicates the discount rate used is too low. The true internal rate of return is interpolated by following the method suggested by Gittinger (1972).

The lower discount rate is 11 per cent and the difference between the two discount rates (11 and 16 per cent) is 5 per cent. The present value of the net income (benefit) at the lower discount rate of 11 per cent is 14. The sum of the absolute value of the present worth of the net income at the two discount rates is 14 + 11 = 25. Therefore

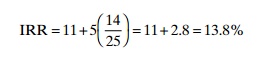
It has been suggested that the interval between discount rates should not be more than 5 per cent. The interpolated rate of return usually overstates the true return (Shang, 1979). In financial analysis, the internal rate of return is often calculated on equity. In this case, payments of interest and amortization are treated as cash outlays, and the borrowed capital as receipts.

Cash flow analysis

In any investment project, it is important to examine the interaction between the average rate of return or rentability and liquidity. Good rentability and high profits do not necessarily involve liquidity. This is particularly important in aquaculture, because of the relatively long gestation period of the projects and the scarcity of venture capital. All available equity and credits may be exhausted before the flow of income becomes large enough to balance the outflow of expenses. If such a situation arises and the project is left without funds to meet operating costs, it is bound to fail, even though it is potentially viable. It is therefore very important to project realistic annual cash flows, to ensure appropriate financing according to an operational schedule and to implement a proper balance of expenditure and income to meet business conditions.

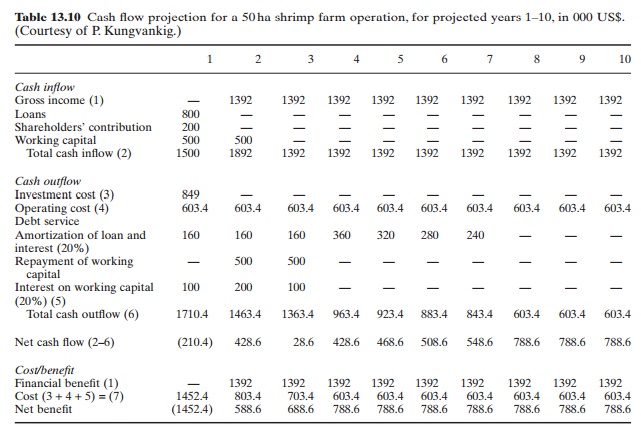
The projected cash flow of an investment project for shrimp farming is given in Table 13.10 as an example. Such estimates help not only in arrangements for financing projects, but also in the selection of farm management systems and technologies most suited from the point of view of project financing.

Socio-economic analysis

While the evaluation of economic performance of aquaculture projects is relatively easy, the estimation of social benefits is much more difficult. Many intangible and unquantifiable benefits are involved. It will often be impractical to separate out aquaculture-derived benefits in communities served by integrated rural development projects. For example, improvement in the nutritional status, employment and income may often be combined with other social development programmes and it is extremely difficult to apportion with any amount of precision the contribution of aquaculture to the combined benefits derived from community activities. Even when it is possible, numerous field studies and collection of data over long periods of time may be needed. When an aquaculture project is designed as the main instrument to meet a specific need of the population it will be easier to evaluate the project’s performance in quantifiable terms.

For example, if a project is designed to upgrade the economic status of a community of 20 families living below the poverty line, the immediate target may be to bring their income to the national average. This may involve, let us say, doubling their present annual income of $600. So, the project may be designed to bring in an annual net income of $1200, which would probably need a pond farm with the capacity to produce about 3 tons of fish annually. In such a project, it should be possible to determine how far the targeted increase in family income has been achieved and what the spill-over effects of these increases have been.

Many of the government-sponsored development programmes often have broader objectives and targets. Besides social benefits, they may be aimed at the overall development of the aquaculture sector. Analysis of such projects cannot therefore be based on purely economic or business criteria. Shang (1981) discussed possible ways of estimating direct benefits and costs of public programmes of aquaculture development and also their secondary benefits and costs.

The direct benefits that can be estimated are the increase in value of outputs or the reduction in production and marketing costs. An increase in value of outputs generally takes place as a result of expansion of production areas, adoption of new technologies, introduction or improvement of credit facilities to farmers or assistance in improving the handling, preservation and marketing of produce. A reduction in production and marketing costs may be achieved by the use of new technologies and assistance in preservation and marketing, as well as by improvement of supporting facilities like hatcheries, feed mills and fertilizer distribution. Projects that are directed towards preventing a predicted reduction in production due to identified reasons have to be evaluated on the basis of the magnitude of production decline that has been prevented.

In the case of aquaculture projects aimed at import substitution or for export to earn foreign exchange, the net benefits will be in terms of net savings or earnings of foreign exchange. If conditions are such that the farm-level prices would not represent the proper prices of the benefits, ‘shadow prices’ will have to be selected. Examples of such situations are

(i) when the government keeps down the domestic price of products through taxation or other means to promote export, and (ii) when the government provides price support to encourage local production. The ‘shadow price’ is the value that reflects the true value of the product to society. In a situation as in (i) the shadow price will be the world market price, and in (ii) a price lower than the existing one, approximating the actual price which would be obtainable under local conditions if there were no government price support.

Estimates of direct costs are relatively easy to make, as they are more readily available. An opportunity cost has often to be included in estimating the cost of production elements, as it reflects the true cost to society. The actual price paid for the project inputs may not be the same as their opportunity cost, and therefore adjustments have to be made in the costs for analysis. An example is the opportunity cost of unskilled labour, who could find other seasonal employment, and labour that needs training and relocation to work on the project. The treatments of costs in socially oriented development and private commercial projects differ in certain respects. For example, a government subsidy is considered a cost to society, but it is

treated as a return in private projects. Interest paid on capital borrowed is a cost in private-sector projects, but is not a cost to society, as it forms a part of the capital returned, which becomes available to the society as a whole. Similarly, taxes and duties are costs to private projects, but these are incomes to society.

Estimation of indirect effects should include benefits and costs to other segments of the same sector or to other sectors of the economy. If the spill-over effects of public investment projects affect the output of other producers, this should be taken into account in socio-economic analysis. Examples of adverse effects of aquaculture projects are disadvantages to recreational facilities and pollution of water sources due to farm discharges. Examples of beneficial effects are improvement of nutritional status of communities, reduction in water-borne diseases, stabilization of fish supplies, etc.

Estimation of ‘value added’ by aquaculture in a region can be performed using the benefit and cost data mentioned earlier. Value added consists of payments made in the form of wages, salaries, rent, interest, depreciation and profit. The sum of these payments is useful in assessing the first impact of the project on the local economy. Additional spending and incomes may then be generated and, if the spending pattern is known, the total income generated within the local economy can be calculated by what is known as the ‘income-impact multiplier’. This is a more complex analysis and may not be justified in the case of modest aquaculture projects.

There are differences of opinion regarding the choice of an appropriate social rate of discount for benefits and costs of public investments, but the before-tax marginal rate of return (i.e. the additional earning that could have been made elsewhere or in the private sector) is considered suitable for all practical purposes. This has to be obtained from a central planning agency, as it is difficult to estimate it at the project level.