Two Dimensional Analytical Geometry | Mathematics - Exercise 6.5: Choose the correct answer | 11th Mathematics : UNIT 6 : Two Dimensional Analytical Geometry
Chapter: 11th Mathematics : UNIT 6 : Two Dimensional Analytical Geometry
Exercise 6.5: Choose the correct answer
CHAPTER
: Two Dimensional Analytical Geometry
Choose
the correct or more suitable answer
1. The equation of the locus of the
point whose distance from y-axis is half the distance from origin is
(1) x2 + 3y2 = 0
(2) x2 - 3y2
= 0
(3) 3x2 + y2 = 0
(4)
3x2 - y2 = 0
Solution

2. Which of the following equation is
the locus of (at2, 2at)

(3) x2 + y2 = a2
(4)
y2 = 4ax
Solution
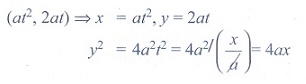
3. Which of the following point lie on
the locus of 3x2 + 3y2 - 8x - 12y + 17 = 0
(1) (0, 0)
(2) (-2, 3)
(3)
(1, 2)
(4) (0,-1)
Solution
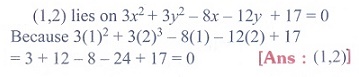
4. If the point (8,-5) lies on the
locus x2/16 - y2/25
= k, then the value of k is
(1) 0
(2) 1
(3) 2
(4)
3
Solution

5. Straight line joining the points (2,
3) and (-1, 4) passes
through the point (α,β) if
(1) α + 2β =7
(2) 3α + β =9
(3)
α + 3β =11
(4) 3α + β =11
Solution
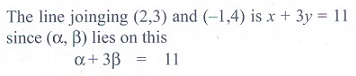
6. The slope of the line which makes an
angle 45̊ with the line 3x -
y = -5 are
(1) 1, -1
(2)
1/2, -2
(3) 1,1/2
(4) 2, -1/2
Solution

7. Equation of the straight line that
forms an isosceles triangle with coordinate axes in the I-quadrant with
perimeter 4 + 2√2 is
(1) x + y + 2 = 0
(2)
x + y - 2
= 0
(3) x + y - √2 = 0
(4) x + y + √2 = 0
Solution
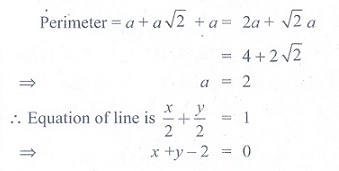
8. The coordinates of the four vertices
of a quadrilateral are (-2,4),
(-1,2), (1,2) and
(2,4) taken in order.The equation of the line passing through the vertex (-1,2) and
dividing the quadrilateral in the equal areas is
(1) x+ 1 = 0
(2) x + y = 1
(3) x + y + 3 = 0
(4)
x - y
+ 3 = 0
Solution

9. The intercepts of the perpendicular
bisector of the line segment joining (1, 2) and (3,4) with
coordinate axes are
(1) 5, -5
(2)
5, 5
(3) 5, 3
(4) 5, -4
Solution

10. The equation of the line with slope
2 and the length of the perpendicular from the origin equal to √5 is
(1) x + 2y = √5
(2) 2x + y = √5
(3)
2x + y = 5
(4) x + 2y - 5 = 0
Solution

11. A line perpendicular to the line 5x - y = 0 forms a
triangle with the coordinate axes. If the area of the triangle is 5 sq. units,
then its equation is
(1)
x+ 5y ± 5√2 = 0
(2) x- 5y ± 5√2 = 0
(3) 5x+y± 5√2 = 0
(4) 5x-y±5√2 = 0
Solution

12. Equation of the straight line
perpendicular to the linex-y+5
= 0, through the point of intersection the y-axis and the given line
(1) x - y - 5 = 0
(2)
x + y - 5
= 0
(3) x + y + 5 = 0
(4) x + y + 10 = 0
Solution
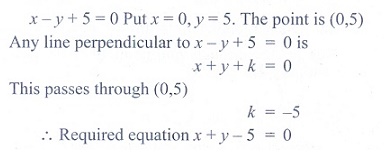
13. If the equation of the base opposite
to the vertex (2, 3) of an equilateral triangle is x + y = 2, then the length
of a side is
(1) √ 3/2
(2) 6
(3)
√6
(4) 3√2
Solution

14. The line (p + 2q)x + (p - 3q)y = p - q for different
values of p and q passes through the point
(1) (3/2, 5/2)
(2) (2/5, 2/5)
(3) (3/5, 3/5)
(4)
(2/5, 3/5)
Solution
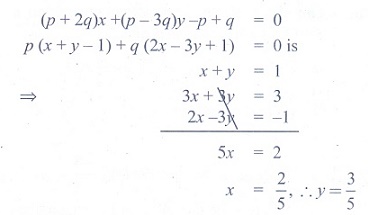
15. The point on the line 2x - 3y = 5 is
equidistance from (1,2) and (3, 4) is
(1) (7, 3)
(2)
(4, 1)
(3) (1,-1)
(4) (-2, 3)
Solution
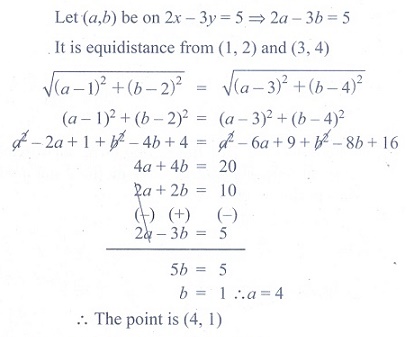
16. The image of the point (2, 3) in the
line y = -x is
(1)
(-3,
-2)
(2) ( -3, 2 )
(3) ( -2, -3)
(4) ( 3, 2 )
Solution
17. The length of ┴ from the origin to the line x/3 – y/4 = 1, is
(1) 11/5
(2) 5/12
(3)
12/5
(4) -5/12
Solution
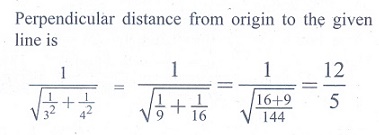
18. The y-intercept of the straight line
passing through (1,3) and perpendicular to 2x - 3y + 1 = 0 is
(1) 3/2
(2)
9/2
(3) 2/3
(4) 2/9
Solution

19. If the two straight lines x + (2k - 7)y + 3 = 0 and
3kx + 9y - 5 = 0 are
perpendicular then the
value of k is
(1)
k = 3
(2) k = 1/3
(3) k = 2/3
(4) k = 3/2
Solution

20. If a vertex of a square is at the
origin and its one side lies along the line 4x + 3y - 20 = 0, then the
area of the square is
(1) 20 sq. units
(2)
16 sq. units
(3) 25 sq. units
(4) 4 sq.units
Solution

21. If the lines represented by the
equation 6x2 + 41xy -
7y2 = 0 make angles
and
with x- axis then tanα tanβ =
(1)
-6/7
(2) 6/7
(3) -7/6
(4) 7/6
Solution
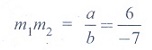
22. The area of the triangle formed by
the lines x2 -
4y2 = 0 and x = a is
(1) 2a2
(2) √3/2 a2
(3)
1/2 a2
(4) 2/√3 a2
Solution
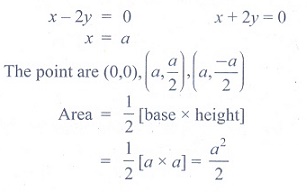
23. If one of the lines given by 6x2
- xy + 4cy2
= 0 is 3x + 4y = 0,, then c equals to
(1)
-3
(2) -1
(3) 3
(4) 1
Solution
24. θ is acute angle between the lines x2
- xy - 6y2
= 0, then 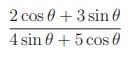 is
is
(1) 1
(2) -1/9
(3)
5/9
(4) 1/9
Solution
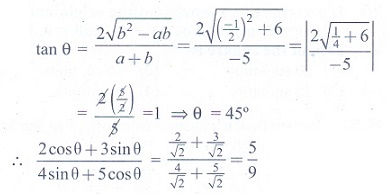
25. The equation of one the line
represented by the equation x2 + 2xy cotθ - y2 =
0 is
(1) x - y cot θ = 0
(2) x + y tan θ = 0
(3) x cos θ + y (sinθ + 1) = 0
(4)
x sin θ + y (cosθ + 1) = 0
Solution
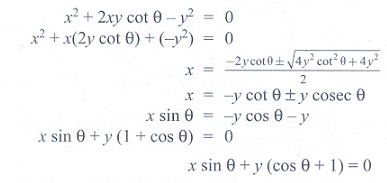
Related Topics