Straight Lines

Straight Lines

Linear equations can be rewritten using the laws of elementary algebra into several different forms. These equations are often referred to as the “equations of the straight line.”

In the general form the linear equation is written as:

ax + by + c = 0       .......................6.4

where a and b are not both equal to zero. The name “linear” comes from the fact that the set of solutions of such an equation forms a straight line in the plane. In this chapter “line”, we mean a straight line unless otherwise stated.

There are many ways to write the equation of a line which can all be converted from one to another by algebraic manipulation. These forms are generally named by the type of information (data) about the line that is needed to write down the form. Some of the important data are points, slope, and intercepts

1. The relationship between the angle of inclination and slope

The slope of a line in the plane containing the x and y axes, is generally represented by the letter m.

It can be measured in many ways as given below:

(i) When θ is the angle of inclination of the line with the x-axis measured in the counter clockwise direction then the slope

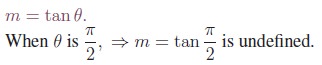
(ii) When (x1, y1) and (x2, y2) are any two points on the line with x2 ¹ x1, then the slope is the change in the y coordinate divided by the corresponding change in the x coordinate.

This is described by the following equation.

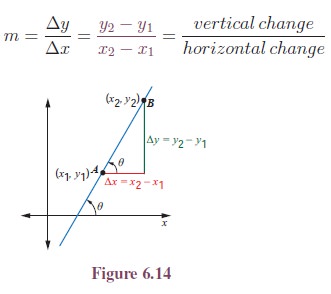
(iii) When the general form of the linear equation ax + by + c = 0 is given, then the slope of the line is

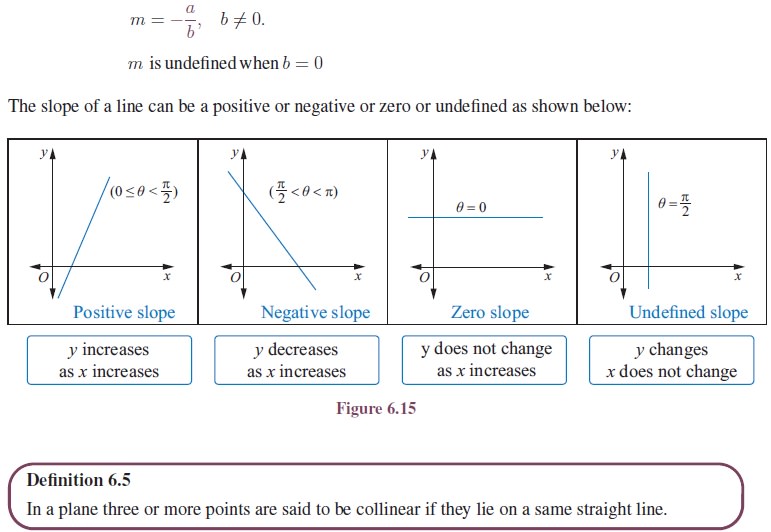
Let A, Band C be any three points on a plane. If the slope of AB is equal to the slope of BC (or AC), then they are collinear.

2. Intercepts of a Line

The x-intercept is a point where the y value is zero, and the y-intercept is a point where the x-value is zero.

Therefore the intercepts of a line are the points where the line intersects, or crosses, the horizontal and vertical axes.

Therefore it is clear that

1.     the equation of the y-axis is x = 0.

2.     the equation of the x-axis is y = 0.

In the figure OA is the x-intercept and OB is the y-intercept.

Different types of x and y Intercepts:

We have learnt the definition and detailed information about the points, slope and intercepts. Using these information, let us recall the different forms of an equation of a straight line.

3. Different Forms of an equation of a straight line

Two conditions are sufficient to determine uniquely the equation of a straight line. Using the combination of any two information from slope, intercepts and points, we can now form different types of straight lines such as

i.            Slope and intercept form

ii.            Point and Slope form

iii.            The two Point form

iv.            Intercepts form and two more special types are

v.            Normal form

vi.            Parametric form

Now let us look at an important way of describing the relationship between two quantities using the notion of a function.

(i)Slope and Intercept form

Proportional linear functions can be written in the form y = mx, where m is the slope of the line. Non proportional linear functions can be written in the form

y = m x + b,   b ¹ 0       .........................6.5

This is called the slope-intercept form of a straight line because m is the slope and b is the y-intercept.

(ii) Point - Slope form:

Let m be the slope of the line and A (x1, y1) be the given point on the line. Let P (x, y) be any point other than A on the given line. Slope of the line joining A (x1, y1) and P (x, y) is given by 

(iii) Two Points form

(iv) Intercepts form:

If the intercepts of a line on thex-axis and the y-axis are known then the equation of the line can also be found using intercepts. Suppose x-intercept OA = a and y-intercept OB = b, where a and b are non-zero, then the line passes through two points A (a, 0) and B (0, b) is

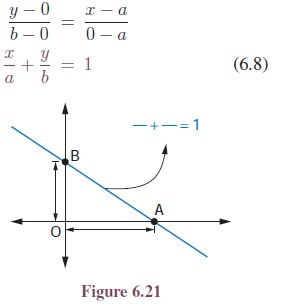
The above equation is called an intercept form.

Lines that pass through the origin or which are horizontal or vertical or violate the nonzero condition on a or b cannot be represented in this form.

In most of the cases this form is used to draw the graph of the line in easy way.

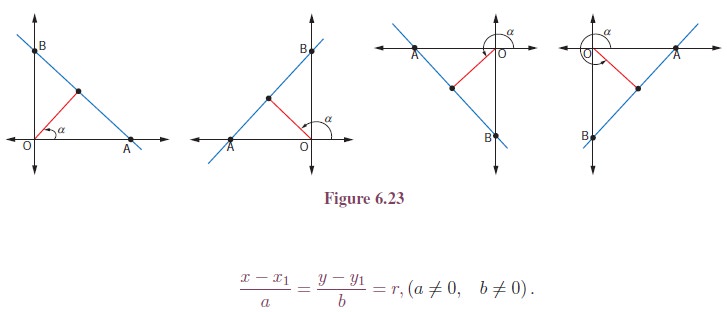
(v) Normal form:

Let A and B be the intercepts made by the line.

Let p be the length of the normal OP drawn from the origin to a line AB, which makes an angle α with the x-axis.

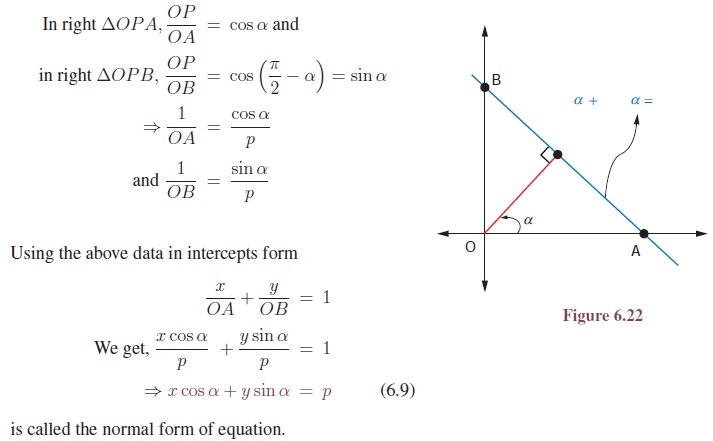
If p is positive in all positions of the line and if α is always measured from x-axis in the positive direction, this equation holds in every case as shown in the figure

(vi) Parametric form:

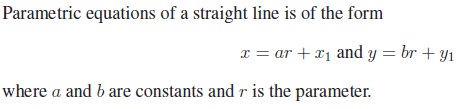
Suppose we have the equation of the line passing through the point Q (x1, y1) and mak-ing an angle θ with x-axis. Let P (x, y) be a point on the line at a distance r from Q. Drop perpendiculars QN and PM respectively from Q andP to the x-axis and perpendicular QR to PM.

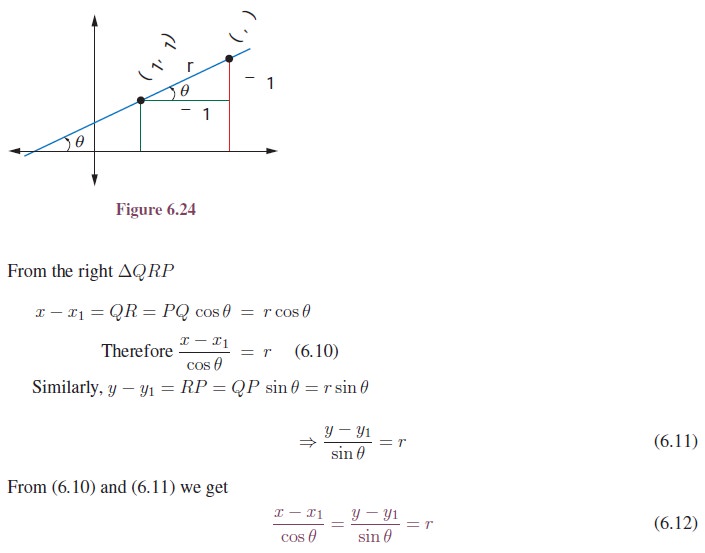
where the parameter r is the distance between (x1, y1) and any point (x, y) on the line. This is called the symmetric form or parametric form of the line.

If we have two variable quantities, then each can be represented by a variable. If the rate of change of one variable with respect to the other variable is constant, then the relationship between them is linear.

In linear equation, the choice of one as independent and other as a dependent may represent the physical reality or may be convenient fiction. The independent variable is normally plotted on the horizontal axis (x-axis), the dependent variable on the vertical axis (y-axis). That is the values of x are always independent and y is dependent on those values of x.

The number scales on the two axes need not be the same. Indeed, in many applications different quantities are represented by x and y. For example, x may represent the number of mobile phones sold and y the total revenue resulting from the sales. In such cases it is often desirable to choose different number scales to represent the different quantities. However, that the zero of both number scales coincide at the origin of the two-dimensional coordinate system.

From the given information, to solve the problem using the concepts of straight lines, we have to select suitably one of the six equations given above.

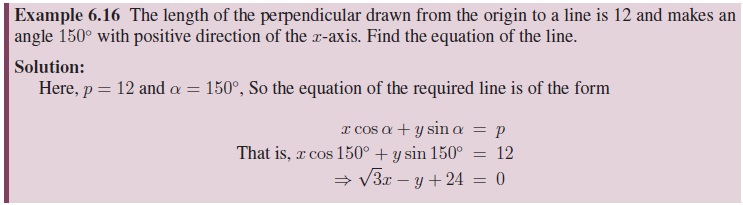
4. General form to other forms

Ax + By + C = 0, where A, B and C being real numbers and A and B cannot be simultaneously equal to zero, can be expressed in terms of A, B and C of the general form into other forms.