Definition, Equation Formula, Solved Example Problems, Exercise | Analytical Geometry | Mathematics - Angle between two straight lines | 11th Mathematics : UNIT 6 : Two Dimensional Analytical Geometry
Chapter: 11th Mathematics : UNIT 6 : Two Dimensional Analytical Geometry
Angle between two straight lines
Angle between two straight lines
Two straight lines in a plane
would either be parallel or coincide or intersect. Normally when two straight
lines intersect, they form two angles at the point of intersection. One is an
acute angle and another is an obtuse angle or equal. Both these angles would be
supplements(Sum equals 180◦) of each other. By definition,
when we say ‘angle between two straight lines’ we mean the acute angle
between the two lines.
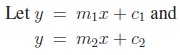
be the equations of
two straight lines and let these two lines make angles θ1and θ2 with x- axis.

1. Condition for Parallel Lines

2. Condition for perpendicular Lines

3. Position of a point with respect to a straight line
Any line ax + by + c =
0 (c = 0),divides the whole
plane in to two parts:
(i) one containing the origin called origin
side of the line and
(ii) the other not containing the origin
called non-origin side of the line.
A point P (x1, y1) is on the origin side or non-origin side of the line ax + by + c =
0 (c ¹
0), according as ax1 + by1 + c and c are of the same sign or opposite sign.
If c > 0, then P (x1, y1) is on the origin side or non orign side of the line ax + by + c =
0 , according as ax1 + by1 + c is positive or
negative.

4. Distance Formulas
Let us develop formulas to find
the distance between
i.
two points
ii.
a point to a line
iii.
two parallel lines
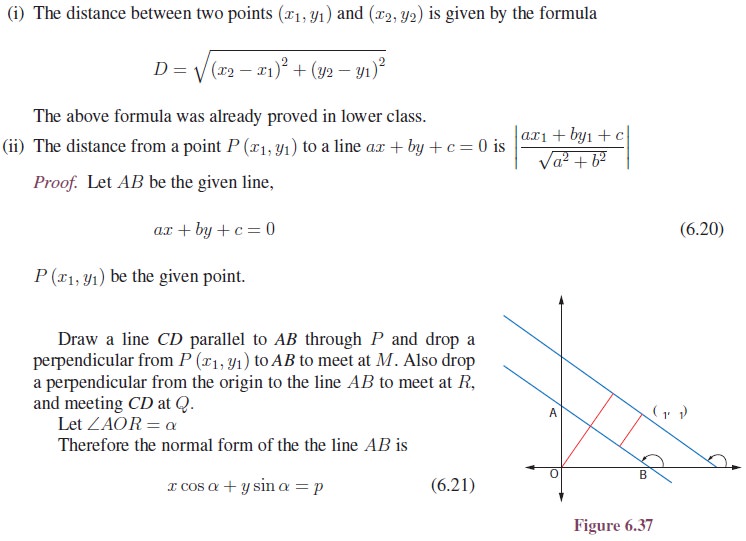







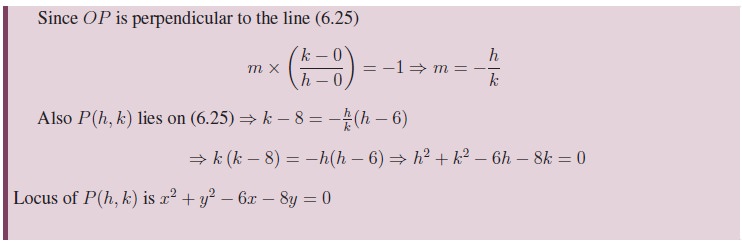
This result shows from the fact
that the angle in a semi circle is a right angle.
5. Family of lines
All lines follow a
specific condition are called a family of lines. The following example shows
some families of straight lines.(where m.h, and k are arbitrary constants).
It may seem that the
equation of a straight line ax + by + c = 0 contains three arbitrary constants. In fact,
it is not so. On dividing it by b (or a, whichever is non-zero), we get

The above equation can
be written as slope and intercept form.
It follows that the
equation of a straight line contains two arbitrary constants, and the number of
these arbitrary constants cannot be decreased further. Thus, the equation of
every straight line contains two arbitrary constants; consequently, two
conditions are needed to determine the equation of a straight line uniquely.
One condition yields a
linear relation among two arbitrary constants and hence each arbitrary constant
determines the other. Therefore, the lines which satisfy one condition contain
a single arbitrary constant. Such a system of lines is called one parameter
family of lines and the unknown arbitrary constant is called, the parameter.
Let us now discuss the
three types of families of straight lines, using y = mx + b. First two types are
one parameter families and third one is two parameters families
·
when m is arbitrary and b is a fixed constant.
·
when b is arbitrary and m is a fixed constant.
·
when both m and b are arbitrary
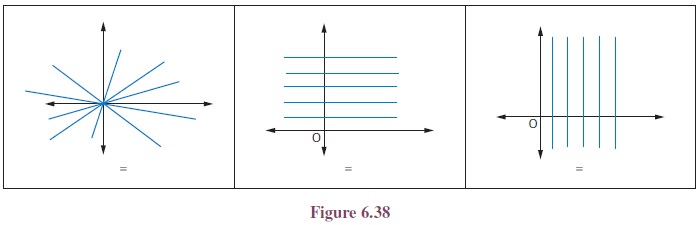
6. One parameter families
(i) when m is arbitrary and b is a fixed constant

Let us find the family
of equations of straight lines for the line y = m x + b by considering m is arbitrary constant and b is a fixed constant
say b = 5. Therefore the equation, for different real values
of m, represents a family of lines with y-intercept 5 units. A
few members of this family are shown in figure. For example, in this diagram
the slope m takes -1, -2, 1/3, 1 and 4.

(ii) when b is arbitrary and m is a fixed constant.
As discussed above,
suppose b is arbitrary constant and m is a fixed constant
say m = −2,the equation y = m x + b becomes = −2x + b. For different real values of b,
a family of lines
can be obtained with
slope −2. A few members of this family are shown in the figure. For
example, in this diagram b can take values −3, −1,
0, 1, 2, 3 and 4.
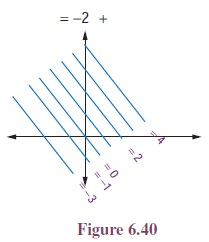
Two special cases
family of parallel lines and family of perpendicular lines are given below

7. Two parameters families



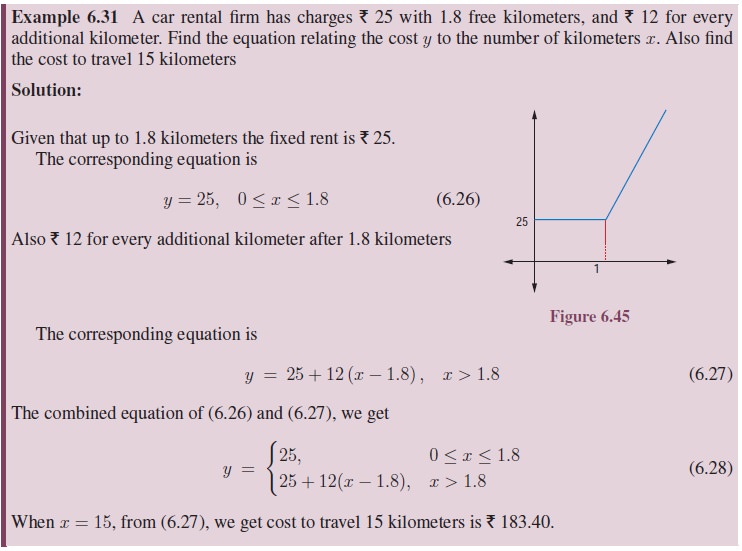



Related Topics